Волновая функция Лафлина
В физике конденсированного состояния волновая функция Лафлина [1] [2] — это анзац , предложенный Робертом Лафлином для основного состояния двумерного электронного газа, помещенного в однородное фоновое магнитное поле при наличии однородного фона желе , когда фактор заполнения нижнего уровня Ландау равен где является нечетным положительным целым числом. Он был построен для объяснения наблюдения дробный квантовый эффект Холла (ДКЭХ) и предсказал существование дополнительных состояния, а также возбуждения квазичастиц с дробным электрическим зарядом , оба из которых позже были обнаружены экспериментально. За это открытие Лафлин получил треть Нобелевской премии по физике в 1998 году.
Контекст и аналитическое выражение
[ редактировать ]Если мы игнорируем желе и взаимное кулоновское отталкивание между электронами в качестве приближения нулевого порядка, мы имеем бесконечно вырожденный нижний уровень Ландау (LLL) и с коэффициентом заполнения 1/ n мы ожидаем, что все электроны будут лежать в ЛЛЛ. Включив взаимодействия, мы можем сделать приближение, что все электроны лежат в LLL. Если — одночастичная волновая функция состояния LLL с наименьшим орбитальным угловым моментом , тогда анзац Лафлина для многочастичной волновой функции равен
где позиция обозначается
в ( гауссовых единицах )
и и — координаты в плоскости x–y. Здесь – приведенная постоянная Планка , – заряд электрона , - общее число частиц, а — магнитное поле , перпендикулярное плоскости xy. Индексы у z идентифицируют частицу. Чтобы волновая функция описывала фермионы , n должно быть нечетным целым числом. Это заставляет волновую функцию быть антисимметричной при обмене частицами. Угловой момент для этого состояния равен .
Истинное основное состояние в ДКЭХ при ν = 1/3
[ редактировать ]Учитывать выше: результат – пробная волновая функция; оно не точно, но качественно воспроизводит многие черты точного решения и количественно имеет очень высокую перекрывается с точным основным состоянием для небольших систем. Предполагая кулоновское отталкивание между любыми двумя электронами, то основное состояние можно определить с помощью точной диагонализации [3] иперекрытия были рассчитаны как близкие к единице. Более того, при короткодействующем взаимодействии (псевдопотенциалы Холдейна для установить на ноль),Волновая функция Лафлина становится точной: [4] т.е. .
Энергия взаимодействия двух частиц
[ редактировать ]
Волновая функция Лафлина — это многочастичная волновая функция для квазичастиц . Среднее значение энергии взаимодействия пары квазичастиц равно
где экранированный потенциал (см. Статические силы и обмен виртуальными частицами § Кулоновский потенциал между двумя токовыми петлями, заключенными в магнитном поле )
где является вырожденной гипергеометрической функцией и является функцией Бесселя первого рода. Здесь, - расстояние между центрами двух токовых петель, - величина заряда электрона , — квантовая версия ларморовского радиуса , и – толщина электронного газа в направлении магнитного поля. Угловые моменты двух отдельных токовых петель равны и где . Длина обратного экранирования определяется выражением ( гауссовы единицы )
где – циклотронная частота , а – площадь электронного газа в плоскости xy.
Энергия взаимодействия оценивается как:
Для получения этого результата мы сделали замену переменных интегрирования
и
и отметил (см. Общие интегралы в квантовой теории поля )
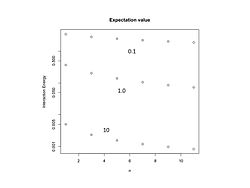
Энергия взаимодействия имеет минимумы при (рис. 1)
и
Для этих значений отношения угловых моментов энергия представлена на рис. 2 в зависимости от .
Ссылки
[ редактировать ]- ^ Лафлин, РБ (2 мая 1983 г.). «Аномальный квантовый эффект Холла: несжимаемая квантовая жидкость с дробно заряженными возбуждениями». Письма о физических отзывах . 50 (18). Американское физическое общество (APS): 1395–1398. Бибкод : 1983PhRvL..50.1395L . дои : 10.1103/physrevlett.50.1395 . ISSN 0031-9007 .
- ^ З.Ф. Эзева (2008). Квантовые эффекты Холла, второе издание . Всемирная научная. ISBN 978-981-270-032-2 . стр. 210-213
- ^ Ёсиока, Д. (2 мая 1983 г.). «Основное состояние двумерных электронов в сильных магнитных полях». Письма о физических отзывах . 50 (18). Американское физическое общество (APS): 1219. doi : 10.1103/physrevlett.50.1219 . ISSN 0031-9007 .
- ^ Холдейн, FDM; Э. Х. Резайи. «Конечные исследования несжимаемого состояния дробно-квантованного эффекта Холла и его возбуждений». Письма о физических отзывах . 54 : 237. doi : 10.1103/PhysRevLett.54.237 .





![{\displaystyle \langle z_{1},z_{2},z_{3},\ldots,z_{N}\mid n,N\rangle =\psi _{n,N}(z_{1},z_ {2},z_{3},\ldots ,z_{N})=D\left[\prod _{N\geqslant i>j\geqslant 1}\left(z_{i}-z_{j}\right )^{n}\right]\prod _{k=1}^{N}\exp \left(-\mid z_{k}\mid ^{2}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2500bd725cdb2da0c016b6be9e3ffebe1b5790f)







































![{\displaystyle {1 \over \left(2\pi \right)^{2}\;2^{2n}\;n!}\int d^{2}z_{1}\;d^{2} z_{2}\;\mid z_{1}-z_{2}\mid ^{2n}\;\exp \left[-2\left(\mid z_{1}\mid ^{2}+\mid z_{2}\mid ^{2}\right)\right]\;{\mathcal {J}}_{0}\left({\sqrt {2}}\;{k\mid z_{1}- z_{2}\mid }\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c2d3b7f868aba752a4ef9c00749b9bf7bfc5511)
![{\displaystyle {1 \over \left(2\pi \right)^{2}\;2^{n}\;n!}\int d^{2}u_{12}\;d^{2} v_{12}\;\mid u_{12}\mid ^{2n}\;\exp \left[-2\left(\mid u_{12}\mid ^{2}+\mid v_{12}\ Mid ^{2}\right)\right]\;{\mathcal {J}}_{0}\left({2}k\mid u_{12}\mid \right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b96ab64f1028a97d4c44a6ea8592a52198bb1f47)


