Клемпер розетка

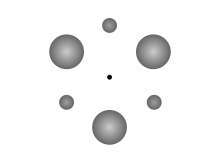
Розетка Клемперера — это гравитационная система (необязательно) чередующихся более тяжелых и легких тел, вращающихся по симметричной орбите вокруг общего барицентра . Впервые он был описан В.Б. Клемперером в 1962 году. ^[1] и является частным случаем центральной конфигурации .

Клемперер описал системы розеток следующим образом:

Такой симметрией обладает также своеобразное семейство геометрических конфигураций, которые можно назвать «розетками». В них четное количество «планет» двух (или более) видов, одна (или несколько) тяжелее другой, но все из каждого набора имеют одинаковую массу, расположены в углах двух (или более) встречно-гребенчатых правильных многоугольников. так, чтобы более легкие и тяжелые чередовались (или циклически следовали друг за другом). ^[1]^{(с. 163)}

Простейшая розетка представляет собой серию из четырех чередующихся более тяжелых и легких тел, расположенных под углом 90 градусов друг к другу, в ромбической конфигурации [Тяжелое, Легкое, Тяжелое, Легкое], где два больших тела имеют одинаковую массу, а также два меньших тела. тела имеют одинаковую массу и все вращаются вокруг своего (пустого) геометрического центра. Более общая троянская система имеет неравные массы двух более тяжелых тел, которую Клемперер также называет «ромбической» системой и которая является единственной версией, не симметричной относительно гравитационного центра.

Количество «массовых типов» можно увеличить при условии, что расположение будет симметричным и циклическим: например, [ 1,2,3 ... 1,2,3 ], [ 1,2,3,4,5 . .. 1,2,3,4,5 ], [ 1,2,3,3,2,1 ... 1,2,3,3,2,1 ] и т.д.

В статье Клемперера конкретно анализируются правильные многоугольники с 2–9 углами ( от гантелей до девятиугольников ) и нецентрально-симметричные « ромбические среднего вращающегося тела розетки» с тремя вращающимися телами, два внешних из которых расположены в треугольных точках (L4 и L5), что уже был описан и изучен Лагранжем в 1772 году. ^[2]Системы с четным числом 4 и более углов могут иметь чередующиеся тяжелые и легкие массы в углах, хотя возможный диапазон соотношений масс ограничен требованиями парастабильности; системы с нечетным числом углов должны иметь равные массы в каждом углу.Хотя Клемперер отмечает, что все розетки и ромб уязвимы для дестабилизации, шестиугольная розетка является наиболее стабильной, поскольку «планеты» располагаются в полустабильных треугольных лагранжевых точках друг друга , L4 и L5. ^[1]^{(с. 165)}

Правильные многоугольные конфигурации («розетки») не требуют центральной массы («солнце» в центре необязательно, и, если оно присутствует, оно может покачиваться выше и ниже плоскости орбиты), хотя ромб типа Лагранжа требует. Если присутствует центральное тело, его масса ограничивает диапазон отношения масс между телами, вращающимися по орбите. ^[1]

Неправильное использование и орфографическая ошибка

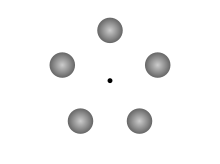
Термин «розетка Клемперера» (часто пишется с ошибкой « розетка Кемплера ») часто используется для обозначения конфигурации из трех или более равных масс, установленных в точках равностороннего многоугольника и имеющих равную угловую скорость относительно их центра масс . Клемперер действительно упоминает эту конфигурацию в начале своей статьи, но только как уже известный набор равновесных систем, прежде чем вводить настоящие розетки.

В Ларри Нивена романе «Флот миров в Мир-кольцо серии » Кукловодов » одноименный « « Флот миров устроен в такой конфигурации. ^[а]который Нивен называет «розеткой Кемплера»; эта (возможно, намеренная) орфографическая ошибка является одним из возможных источников более широкой путаницы. Примечательно, что эти вымышленные планеты удерживались на месте с помощью больших двигателей, а также силы гравитации.

нестабильность

Как простой анализ линейных возмущений, так и моделирование розеток. ^[4] демонстрируют, что такие системы нестабильны: Клемперер объясняет в своей оригинальной статье, что любое отклонение от идеально симметричной геометрии вызывает растущее колебание, что в конечном итоге приводит к разрушению системы. ^[1]^{(стр. 165–166)} Система нестабильна независимо от того, находится ли центр розетки в свободном пространстве или на орбите вокруг центральной звезды.

Краткая причина нестабильности заключается в том, что любое возмущение нарушает геометрическую симметрию, что увеличивает возмущение, что еще больше подрывает геометрию и так далее. Более длинное объяснение состоит в том, что любое тангенциальное возмущение приближает тело к одному соседу и отдаляет от другого; гравитационный дисбаланс становится больше по направлению к более близкому соседу и меньше к дальнему соседу, притягивая возмущенный объект дальше к его более близкому соседу, усиливая возмущение, а не ослабляя его. Внутреннее радиальное возмущение заставляет возмущенное тело приближаться ко всем другим объектам, увеличивая силу, действующую на объект, и увеличивая его орбитальную скорость, что косвенно приводит к тангенциальному возмущению и приведенному выше аргументу. ^[б]

Примечания

^ Розетка Клемперера, Нивеном и Лернером описанная в книге «Флот миров», представляет собой систему из пяти планет, расположенных в вершинах пятиугольника . ^[3] Дженкинс критикует инженерный выбор пяти планет вместо более стабильного шестиугольника из шести планет как нехарактерный для одержимых безопасностью « Кукловодов» Пирсона . ^[4]
^ Из-за гравитационной нестабильности розетка фермерских миров Кукловодов , описанная Нивеном, потребует некоторой формы искусственной стабилизации, которую Нивен и Лернер действительно указывают в «Флоте миров» . ^[3]

Ссылки

^ Jump up to: ^а ^б ^с ^д ^и Клемперер, ВБ (апрель 1962 г.). «Некоторые свойства розеточных конфигураций гравитирующих тел, находящихся в гомографическом равновесии» . Астрономический журнал . 67 (3): 162–167. Бибкод : 1962AJ.....67..162K . дои : 10.1086/108686 .
^ Лагранж, Жозеф-Луи (1772). «Очерк задачи трех тел » (PDF) . Премия Королевской академии наук Парижа (на французском языке). IX . Париж, Франция: Королевская академия наук . Архивировано из оригинала (PDF) 22 декабря 2017 года.
^ Jump up to: ^а ^б Нивен, Ларри ; Лернер, Эдвард (2007). Флот Миров . Нью-Йорк: Tor Books . ISBN 978-0-7653-1825-1 .
^ Jump up to: ^а ^б Дженкинс, Боб. «Розочки Клемперера» . burtleburtle.net . Физика . Проверено 12 января 2007 г.

Внешние ссылки

Дженкинс, Боб. «Розочки Клемперера» . burtleburtle.net . Физика . Проверено 12 января 2007 г. — Моделирование розеток

«Розетка Кемплера (Клемперера) работы Ларри Нивена из Мира Кольца » . technovelgy.com .

[5] Розетка Клемперера, Нивеном и Лернером описанная в книге «Флот миров», представляет собой систему из пяти планет, расположенных в вершинах пятиугольника . ^[3] Дженкинс критикует инженерный выбор пяти планет вместо более стабильного шестиугольника из шести планет как нехарактерный для одержимых безопасностью « Кукловодов» Пирсона . ^[4]

[6] Из-за гравитационной нестабильности розетка фермерских миров Кукловодов , описанная Нивеном, потребует некоторой формы искусственной стабилизации, которую Нивен и Лернер действительно указывают в «Флоте миров» . ^[3]

[Klemperer-1962-1] Jump up to: ^а ^б ^с ^д ^и Клемперер, ВБ (апрель 1962 г.). «Некоторые свойства розеточных конфигураций гравитирующих тел, находящихся в гомографическом равновесии» . Астрономический журнал . 67 (3): 162–167. Бибкод : 1962AJ.....67..162K . дои : 10.1086/108686 .

[Lagrange-1772-2] Лагранж, Жозеф-Луи (1772). «Очерк задачи трех тел » (PDF) . Премия Королевской академии наук Парижа (на французском языке). IX . Париж, Франция: Королевская академия наук . Архивировано из оригинала (PDF) 22 декабря 2017 года.

[Niven-Lerner-2007-3] Jump up to: ^а ^б Нивен, Ларри ; Лернер, Эдвард (2007). Флот Миров . Нью-Йорк: Tor Books . ISBN 978-0-7653-1825-1 .

[Jenkins-kempler-4] Jump up to: ^а ^б Дженкинс, Боб. «Розочки Клемперера» . burtleburtle.net . Физика . Проверено 12 января 2007 г.

[1]

[2]

[а]

[4]

[б]

[3]