Квантовый точечный контакт

Схематический график проводимости точечного контакта в зависимости от напряжения на затворе. Проводимость показывает плато при кратных $2e^{2}/h$

Квантовый точечный контакт ( КТК ) представляет собой узкое сужение между двумя широкими электропроводящими областями, ширина которых сравнима с электронной длиной волны (от нано-микрометра).

Важность КПК заключается в том, что они доказывают квантование баллистической проводимости в мезоскопических системах. Проводимость QPC квантуется в единицах $2e^{2}/h$, так называемый квант проводимости .

О контактах квантовых точек впервые сообщили в 1988 году голландская группа из Делфтского технологического университета и исследовательской компании Philips Research. и независимо британской командой из Кавендишской лаборатории . Они основаны на более ранней работе британской группы, которая показала, как можно использовать разделенные затворы для преобразования двумерного электронного газа в одномерный, сначала в кремнии. а затем в арсениде галлия .

Это квантование напоминает квантование холловской проводимости , но измеряется в отсутствие магнитного поля. Квантование проводимости в нулевом поле и плавный переход к квантовому эффекту Холла при приложении магнитного поля по существу являются следствием равнораспределения тока между целым числом распространяющихся мод в сужении.

Изготовление

Существует несколько различных способов изготовления квантового точечного контакта. Его можно реализовать в разрывном соединении , растягивая кусок проводника до его разрыва. Точка разрыва образует точечный контакт. Более контролируемым образом квантовые точечные контакты формируются в двумерном электронном газе (2DEG), например, в GaAs / AlGaAs гетероструктурах . Подавая напряжение на электроды затвора подходящей формы, электронный газ может быть локально обеднен и в плоскости 2DEG может быть создано множество различных типов проводящих областей, в том числе квантовые точки и квантовые точечные контакты. Другой способ создания QPC — размещение кончика сканирующего туннельного микроскопа близко к поверхности проводника.

Характеристики

Геометрически квантовый точечный контакт представляет собой сужение в поперечном направлении, которое оказывает сопротивление движению электронов . Подача напряжения $V$ через точечный контакт вызывает протекание тока, величина этого тока определяется выражением $I=GV$, где $G$ это проводимость контакта. Эта формула напоминает закон Ома для макроскопических резисторов. Однако здесь есть фундаментальное отличие, обусловленное небольшим размером системы, которое требует квантовомеханического анализа.

Классический баллистический перенос через точечный контакт, вызванный разницей концентраций.

Чистый ток через квантовый точечный контакт, переносимый заштрихованной областью в k -пространстве. Поддиапазоны 1D тогда соответствуют парам горизонтальных линий в точке $k_{y}=\pm n\pi /W$, с n = 1, 2, . . . , N , где N — максимальное количество мод, допускаемое энергией Ферми.

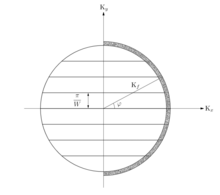
Чаще всего КФХ изучают в двумерных электронных газах. Таким образом, геометрическое ограничение точечного контакта превращает проводимость через отверстие в одномерную систему. Более того, это требует квантовомеханического описания системы, которое приводит к квантованию проводимости. Квантово-механически ток через точечный контакт равномерно распределяется между одномерными подзонами или поперечными модами в сужении.

Важно отметить, что предыдущее обсуждение не учитывает возможные переходы между режимами. Формулу Ландауэра действительно можно обобщить, чтобы выразить возможные переходы.

$G={2e^{2} \over h}\sum _{n,m}|T_{n,m}|^{2}$,

где $T_{n,m}$ — матрица перехода, которая включает в себя ненулевые вероятности передачи из режима n в режим m .

При низких температурах и напряжениях нерассеянные и незахваченные электроны, участвующие в токе, имеют определенную энергию/импульс/длину волны, называемую Ферми энергией /импульсом/длиной волны . Как и в волноводе , поперечное ограничение в контакте квантовой точки приводит к «квантованию» поперечного движения — поперечное движение не может меняться непрерывно, а должно быть одним из ряда дискретных режимов. Аналогия с волноводом применима до тех пор, пока когерентность не теряется из-за рассеяния, например, из-за дефекта или места захвата. Электронная волна может пройти через перетяжку только в том случае, если она конструктивно интерферирует, что при заданной ширине перетяжки происходит только для определенного числа мод. $N$. Ток, переносимый таким квантовым состоянием, является произведением скорости на плотность электронов. Эти две величины сами по себе различаются от одного режима к другому, но их произведение не зависит от режима. Как следствие, каждое государство вносит одинаковую сумму $e^{2}/h$ на направление спина к общей проводимости $G=NG_{0}$.

Это фундаментальный результат; проводимость не принимает произвольных значений, а квантуется кратно кванту проводимости $G_{0}=2e^{2}/h$, который выражается через заряд электрона $e$ и постоянная Планка $h$. Целое число $N$ определяется шириной точечного контакта и примерно равна ширине, разделенной на половину длины волны электрона . В зависимости от ширины точечного контакта (или напряжения на затворе в случае гетероструктурных устройств GaAs/AlGaAs) проводимость демонстрирует лестничное поведение, поскольку все больше и больше мод (или каналов) вносят вклад в транспорт электронов. Высота ступеньки определяется выражением $G_{Q}$.

При повышении температуры экспериментально обнаруживают, что плато приобретают конечный наклон до тех пор, пока не перестанут разрешаться. Это следствие теплового размытия распределения Ферми-Дирака . Ступени проводимости должны исчезнуть при $T\lesssim \Delta E/4k_{\rm {B}}\approx 4\;\mathrm {K}$ (здесь ∆E — расщепление подзоны на уровне Ферми ). Это подтверждено как экспериментом, так и численными расчетами.

Внешнее магнитное поле, приложенное к контакту квантовой точки, снимает спиновое вырождение и приводит к полуцелым шагам проводимости. Кроме того, число $N$ мод, вносящих вклад, становится меньше. Для больших магнитных полей $N$ не зависит от ширины перетяжки, заданной теорией квантового эффекта Холла .

Аномалия 0,7

Аномальные особенности на квантованных ступенях проводимости часто наблюдаются при транспортных измерениях квантовых точечных контактов. Ярким примером является плато в $0.7G_{Q}$, так называемая 0,7-структура, возникающая за счет усиленных электрон-электронных взаимодействий, возникающих из-за размытой сингулярности Ван Хова в локальной одномерной плотности состояний в окрестности зарядового пережима. В отличие от ступеней проводимости, 0,7-структура становится более выраженной при более высокой температуре. Аналоги 0,7-структуры иногда наблюдаются на более высоких ступенях проводимости. Квазисвязанные состояния, возникающие из-за примесей, зарядовых ловушек и отражений внутри сужения, также могут приводить к структуре проводимости, близкой к 1D-пределу.

Приложения

Помимо изучения основ переноса заряда в мезоскопических проводниках, квантовые точечные контакты могут использоваться в качестве чрезвычайно чувствительных детекторов заряда. Поскольку проводимость через контакт сильно зависит от размера перетяжки, любые колебания потенциала (например, создаваемые другими электронами) поблизости будут влиять на ток через КПК. С помощью такой схемы можно обнаружить одиночные электроны. С точки зрения квантовых вычислений в твердотельных системах КПК можно использовать в качестве устройств считывания состояния квантового бита (кубита). В физике устройств конфигурация QPC используется для демонстрации полностью баллистического полевого транзистора. Еще одним применением устройства является его использование в качестве выключателя. Никелевую проволоку подносят достаточно близко к золотой поверхности, а затем с помощью пьезоэлектрического привода можно изменить расстояние между проволокой и поверхностью, и, таким образом, транспортные характеристики устройства изменяются между туннельными электронами и баллистическими.

Дальнейшее чтение

• CWJBeenakker и Х. ван Хаутен (1991). «Квантовый транспорт в полупроводниковых наноструктурах». Физика твердого тела . 44 : 1–228. arXiv : cond-mat/0412664 . Бибкод : 2004cond.mat.12664B . дои : 10.1016/s0081-1947(08)60091-0 . ISBN  9780126077445 . S2CID   119082619 .
• К. Дж. Томас; и др. (1996). «Возможная спиновая поляризация в одномерном электронном газе». Письма о физических отзывах . 77 (1): 135–138. arXiv : cond-mat/9606004 . Бибкод : 1996PhRvL..77..135T . дои : 10.1103/PhysRevLett.77.135 . ПМИД   10061790 . S2CID   8903637 .
• Николас Аграит; Альфредо Леви Йеяти; Ян М. ван Рейтенбек (2003). «Квантовые свойства проводников атомного размера». Отчеты по физике . 377 (2–3): 81. arXiv : cond-mat/0208239 . Бибкод : 2003ФР...377...81А . дои : 10.1016/S0370-1573(02)00633-6 . S2CID   119409385 .
• Тимп, Г. (1992). «Глава 3: Когда провод становится электронным волноводом». Полупроводники и полуметаллы Том 35 . Том. 35. стр. 113–190. дои : 10.1016/S0080-8784(08)62393-5 . ISBN  9780127521350 .