Производные механике скаляров по , векторов второго порядка и тензоров тензорам второго порядка находят значительное применение в сплошных сред . Эти производные используются в теориях нелинейной упругости и пластичности , в частности при разработке алгоритмов численного моделирования . [1]
Производная по направлению обеспечивает систематический способ поиска этих производных. [2]
Производные по векторам и тензорам второго порядка [ редактировать ] Ниже приведены определения производных по направлению для различных ситуаций. Предполагается, что функции достаточно гладкие, чтобы можно было брать производные.
Пусть f ( v ) — вещественная функция вектора v . Тогда производная f ( v ) по v (или по v ) — это вектор, определенный через его скалярное произведение , где любой вектор u равен
∂ f ∂ v ⋅ u = D f ( v ) [ u ] = [ d d α f ( v + α u ) ] α = 0 {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}
для всех векторов u . Вышеупомянутое скалярное произведение дает скаляр, и если u является единичным вектором, дает производную по направлению от f в точке v в направлении u .
Характеристики:
Если f ( v ) = f 1 ( v ) + f 2 ( v ) {\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )+f_{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v + ∂ f 2 ∂ v ) ⋅ u {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}+{\frac {\partial f_{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u} } Если f ( v ) = f 1 ( v ) f 2 ( v ) {\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )~f_{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v ⋅ u ) f 2 ( v ) + f 1 ( v ) ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)~f_{2}(\mathbf {v} )+f_{1}(\mathbf {v} )~\left({\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)} Если f ( v ) = f 1 ( f 2 ( v ) ) {\displaystyle f(\mathbf {v} )=f_{1}(f_{2}(\mathbf {v} ))} ∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ∂ f 2 ∂ v ⋅ u {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial f_{1}}{\partial f_{2}}}~{\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} } Пусть f ( v ) — вектор-функция вектора v . Тогда производная f ( v ) по v (или по v ) представляет собой тензор второго порядка, определенный через его скалярное произведение, где любой вектор u равен
∂ f ∂ v ⋅ u = D f ( v ) [ u ] = [ d d α f ( v + α u ) ] α = 0 {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}
для всех векторов u . Вышеупомянутое скалярное произведение дает вектор, и если u является единичным вектором, дает производную направления f в v в направлении u .
Характеристики:
Если f ( v ) = f 1 ( v ) + f 2 ( v ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )+\mathbf {f} _{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v + ∂ f 2 ∂ v ) ⋅ u {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}+{\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u} } Если f ( v ) = f 1 ( v ) × f 2 ( v ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )\times \mathbf {f} _{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v ⋅ u ) × f 2 ( v ) + f 1 ( v ) × ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)\times \mathbf {f} _{2}(\mathbf {v} )+\mathbf {f} _{1}(\mathbf {v} )\times \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)} Если f ( v ) = f 1 ( f 2 ( v ) ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {f} _{2}(\mathbf {v} ))} ∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ⋅ ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {f} _{2}}}\cdot \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)} Производные скалярнозначных функций тензоров второго порядка [ редактировать ] Позволять f ( S ) {\displaystyle f({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} f ( S ) {\displaystyle f({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} S {\displaystyle {\boldsymbol {S}}} T {\displaystyle {\boldsymbol {T}}} тензор второго порядка, определяемый как ∂ f ∂ S : T = D f ( S ) [ T ] = [ d d α f ( S + α T ) ] α = 0 {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}} T {\displaystyle {\boldsymbol {T}}}
Характеристики:
Если f ( S ) = f 1 ( S ) + f 2 ( S ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})+f_{2}({\boldsymbol {S}})} ∂ f ∂ S : T = ( ∂ f 1 ∂ S + ∂ f 2 ∂ S ) : T {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}\right):{\boldsymbol {T}}} Если f ( S ) = f 1 ( S ) f 2 ( S ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})~f_{2}({\boldsymbol {S}})} ∂ f ∂ S : T = ( ∂ f 1 ∂ S : T ) f 2 ( S ) + f 1 ( S ) ( ∂ f 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)~f_{2}({\boldsymbol {S}})+f_{1}({\boldsymbol {S}})~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Если f ( S ) = f 1 ( f 2 ( S ) ) {\displaystyle f({\boldsymbol {S}})=f_{1}(f_{2}({\boldsymbol {S}}))} ∂ f ∂ S : T = ∂ f 1 ∂ f 2 ( ∂ f 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial f_{2}}}~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Производные тензорнозначных функций тензоров второго порядка [ редактировать ] Позволять F ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} F ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} S {\displaystyle {\boldsymbol {S}}} T {\displaystyle {\boldsymbol {T}}} тензор четвертого порядка, определяемый как ∂ F ∂ S : T = D F ( S ) [ T ] = [ d d α F ( S + α T ) ] α = 0 {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}} T {\displaystyle {\boldsymbol {T}}}
Характеристики:
Если F ( S ) = F 1 ( S ) + F 2 ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})+{\boldsymbol {F}}_{2}({\boldsymbol {S}})} ∂ F ∂ S : T = ( ∂ F 1 ∂ S + ∂ F 2 ∂ S ) : T {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}\right):{\boldsymbol {T}}} Если F ( S ) = F 1 ( S ) ⋅ F 2 ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})} ∂ F ∂ S : T = ( ∂ F 1 ∂ S : T ) ⋅ F 2 ( S ) + F 1 ( S ) ⋅ ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})+{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Если F ( S ) = F 1 ( F 2 ( S ) ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))} ∂ F ∂ S : T = ∂ F 1 ∂ F 2 : ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Если f ( S ) = f 1 ( F 2 ( S ) ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))} ∂ f ∂ S : T = ∂ f 1 ∂ F 2 : ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Градиент , ∇ T {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}} T ( x ) {\displaystyle {\boldsymbol {T}}(\mathbf {x} )} c определяется как: ∇ T ⋅ c = lim α → 0 d d α T ( x + α c ) {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot \mathbf {c} =\lim _{\alpha \rightarrow 0}\quad {\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(\mathbf {x} +\alpha \mathbf {c} )} n — это тензорное поле порядка n +1.
Если e 1 , e 2 , e 3 {\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}} декартовой системе координат , координаты точек обозначаются ( x 1 , x 2 , x 3 {\displaystyle x_{1},x_{2},x_{3}} T {\displaystyle {\boldsymbol {T}}} ∇ T = ∂ T ∂ x i ⊗ e i {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}\otimes \mathbf {e} _{i}}
Поскольку базисные векторы не меняются в декартовой системе координат, для градиентов скалярного поля имеем следующие соотношения: ϕ {\displaystyle \phi } v и тензорное поле второго порядка S {\displaystyle {\boldsymbol {S}}} ∇ ϕ = ∂ ϕ ∂ x i e i = ϕ , i e i ∇ v = ∂ ( v j e j ) ∂ x i ⊗ e i = ∂ v j ∂ x i e j ⊗ e i = v j , i e j ⊗ e i ∇ S = ∂ ( S j k e j ⊗ e k ) ∂ x i ⊗ e i = ∂ S j k ∂ x i e j ⊗ e k ⊗ e i = S j k , i e j ⊗ e k ⊗ e i {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi &={\cfrac {\partial \phi }{\partial x_{i}}}~\mathbf {e} _{i}=\phi _{,i}~\mathbf {e} _{i}\\{\boldsymbol {\nabla }}\mathbf {v} &={\cfrac {\partial (v_{j}\mathbf {e} _{j})}{\partial x_{i}}}\otimes \mathbf {e} _{i}={\cfrac {\partial v_{j}}{\partial x_{i}}}~\mathbf {e} _{j}\otimes \mathbf {e} _{i}=v_{j,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{i}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\cfrac {\partial (S_{jk}\mathbf {e} _{j}\otimes \mathbf {e} _{k})}{\partial x_{i}}}\otimes \mathbf {e} _{i}={\cfrac {\partial S_{jk}}{\partial x_{i}}}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}=S_{jk,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}\end{aligned}}}
Если g 1 , g 2 , g 3 {\displaystyle \mathbf {g} ^{1},\mathbf {g} ^{2},\mathbf {g} ^{3}} контравариантные базисные векторы в криволинейной системе координат , координаты точек обозначаются ( ξ 1 , ξ 2 , ξ 3 {\displaystyle \xi ^{1},\xi ^{2},\xi ^{3}} T {\displaystyle {\boldsymbol {T}}} [3] ∇ T = ∂ T ∂ ξ i ⊗ g i {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}={\frac {\partial {\boldsymbol {T}}}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}}
Из этого определения мы имеем следующие соотношения для градиентов скалярного поля ϕ {\displaystyle \phi } v и тензорное поле второго порядка S {\displaystyle {\boldsymbol {S}}} ∇ ϕ = ∂ ϕ ∂ ξ i g i ∇ v = ∂ ( v j g j ) ∂ ξ i ⊗ g i = ( ∂ v j ∂ ξ i + v k Γ i k j ) g j ⊗ g i = ( ∂ v j ∂ ξ i − v k Γ i j k ) g j ⊗ g i ∇ S = ∂ ( S j k g j ⊗ g k ) ∂ ξ i ⊗ g i = ( ∂ S j k ∂ ξ i − S l k Γ i j l − S j l Γ i k l ) g j ⊗ g k ⊗ g i {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi &={\frac {\partial \phi }{\partial \xi ^{i}}}~\mathbf {g} ^{i}\\{\boldsymbol {\nabla }}\mathbf {v} &={\frac {\partial \left(v^{j}\mathbf {g} _{j}\right)}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}=\left({\frac {\partial v^{j}}{\partial \xi ^{i}}}+v^{k}~\Gamma _{ik}^{j}\right)~\mathbf {g} _{j}\otimes \mathbf {g} ^{i}=\left({\frac {\partial v_{j}}{\partial \xi ^{i}}}-v_{k}~\Gamma _{ij}^{k}\right)~\mathbf {g} ^{j}\otimes \mathbf {g} ^{i}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\frac {\partial \left(S_{jk}~\mathbf {g} ^{j}\otimes \mathbf {g} ^{k}\right)}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}=\left({\frac {\partial S_{jk}}{\partial \xi _{i}}}-S_{lk}~\Gamma _{ij}^{l}-S_{jl}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{j}\otimes \mathbf {g} ^{k}\otimes \mathbf {g} ^{i}\end{aligned}}}
где символ Кристоффеля Γ i j k {\displaystyle \Gamma _{ij}^{k}} Γ i j k g k = ∂ g i ∂ ξ j ⟹ Γ i j k = ∂ g i ∂ ξ j ⋅ g k = − g i ⋅ ∂ g k ∂ ξ j {\displaystyle \Gamma _{ij}^{k}~\mathbf {g} _{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\quad \implies \quad \Gamma _{ij}^{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\cdot \mathbf {g} ^{k}=-\mathbf {g} _{i}\cdot {\frac {\partial \mathbf {g} ^{k}}{\partial \xi ^{j}}}}
В цилиндрических координатах градиент определяется выражением ∇ ϕ = ∂ ϕ ∂ r e r + 1 r ∂ ϕ ∂ θ e θ + ∂ ϕ ∂ z e z ∇ v = ∂ v r ∂ r e r ⊗ e r + 1 r ( ∂ v r ∂ θ − v θ ) e r ⊗ e θ + ∂ v r ∂ z e r ⊗ e z + ∂ v θ ∂ r e θ ⊗ e r + 1 r ( ∂ v θ ∂ θ + v r ) e θ ⊗ e θ + ∂ v θ ∂ z e θ ⊗ e z + ∂ v z ∂ r e z ⊗ e r + 1 r ∂ v z ∂ θ e z ⊗ e θ + ∂ v z ∂ z e z ⊗ e z ∇ S = ∂ S r r ∂ r e r ⊗ e r ⊗ e r + ∂ S r r ∂ z e r ⊗ e r ⊗ e z + 1 r [ ∂ S r r ∂ θ − ( S θ r + S r θ ) ] e r ⊗ e r ⊗ e θ + ∂ S r θ ∂ r e r ⊗ e θ ⊗ e r + ∂ S r θ ∂ z e r ⊗ e θ ⊗ e z + 1 r [ ∂ S r θ ∂ θ + ( S r r − S θ θ ) ] e r ⊗ e θ ⊗ e θ + ∂ S r z ∂ r e r ⊗ e z ⊗ e r + ∂ S r z ∂ z e r ⊗ e z ⊗ e z + 1 r [ ∂ S r z ∂ θ − S θ z ] e r ⊗ e z ⊗ e θ + ∂ S θ r ∂ r e θ ⊗ e r ⊗ e r + ∂ S θ r ∂ z e θ ⊗ e r ⊗ e z + 1 r [ ∂ S θ r ∂ θ + ( S r r − S θ θ ) ] e θ ⊗ e r ⊗ e θ + ∂ S θ θ ∂ r e θ ⊗ e θ ⊗ e r + ∂ S θ θ ∂ z e θ ⊗ e θ ⊗ e z + 1 r [ ∂ S θ θ ∂ θ + ( S r θ + S θ r ) ] e θ ⊗ e θ ⊗ e θ + ∂ S θ z ∂ r e θ ⊗ e z ⊗ e r + ∂ S θ z ∂ z e θ ⊗ e z ⊗ e z + 1 r [ ∂ S θ z ∂ θ + S r z ] e θ ⊗ e z ⊗ e θ + ∂ S z r ∂ r e z ⊗ e r ⊗ e r + ∂ S z r ∂ z e z ⊗ e r ⊗ e z + 1 r [ ∂ S z r ∂ θ − S z θ ] e z ⊗ e r ⊗ e θ + ∂ S z θ ∂ r e z ⊗ e θ ⊗ e r + ∂ S z θ ∂ z e z ⊗ e θ ⊗ e z + 1 r [ ∂ S z θ ∂ θ + S z r ] e z ⊗ e θ ⊗ e θ + ∂ S z z ∂ r e z ⊗ e z ⊗ e r + ∂ S z z ∂ z e z ⊗ e z ⊗ e z + 1 r ∂ S z z ∂ θ e z ⊗ e z ⊗ e θ {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi ={}\quad &{\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r}+{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi }{\partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} ={}\quad &{\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{r}}{\partial \theta }}-v_{\theta }\right)~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{r}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{\theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{z}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{z\theta }}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}
Дивергенция поля тензорного T ( x ) {\displaystyle {\boldsymbol {T}}(\mathbf {x} )} ( ∇ ⋅ T ) ⋅ c = ∇ ⋅ ( c ⋅ T T ) ; ∇ ⋅ v = tr ( ∇ v ) {\displaystyle ({\boldsymbol {\nabla }}\cdot {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot \left(\mathbf {c} \cdot {\boldsymbol {T}}^{\textsf {T}}\right)~;\qquad {\boldsymbol {\nabla }}\cdot \mathbf {v} ={\text{tr}}({\boldsymbol {\nabla }}\mathbf {v} )}
где c — произвольный постоянный вектор, а v — векторное поле. Если T {\displaystyle {\boldsymbol {T}}} n > 1, то дивергенция поля является тензором порядка n − 1.
В декартовой системе координат мы имеем следующие соотношения для векторного поля v и тензорного поля второго порядка S {\displaystyle {\boldsymbol {S}}} ∇ ⋅ v = ∂ v i ∂ x i = v i , i ∇ ⋅ S = ∂ S i k ∂ x i e k = S i k , i e k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &={\frac {\partial v_{i}}{\partial x_{i}}}=v_{i,i}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\frac {\partial S_{ik}}{\partial x_{i}}}~\mathbf {e} _{k}=S_{ik,i}~\mathbf {e} _{k}\end{aligned}}}
где обозначение тензорного индекса в крайних правых выражениях используется для частных производных. Обратите внимание, что ∇ ⋅ S ≠ ∇ ⋅ S T . {\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}\neq {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}^{\textsf {T}}.}
Для симметричного тензора второго порядка дивергенцию также часто записывают как [4]
∇ ⋅ S = ∂ S k i ∂ x i e k = S k i , i e k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\cfrac {\partial S_{ki}}{\partial x_{i}}}~\mathbf {e} _{k}=S_{ki,i}~\mathbf {e} _{k}\end{aligned}}}
Вышеприведенное выражение иногда используется в качестве определения ∇ ⋅ S {\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}} div S {\displaystyle \operatorname {div} {\boldsymbol {S}}}
Разница заключается в том, по какому принципу дифференцирование производится: по строкам или по столбцам. S {\displaystyle {\boldsymbol {S}}} S {\displaystyle \mathbf {S} } v {\displaystyle \mathbf {v} }
∇ ⋅ ( ∇ v ) = ∇ ⋅ ( v i , j e i ⊗ e j ) = v i , j i e i ⋅ e i ⊗ e j = ( ∇ ⋅ v ) , j e j = ∇ ( ∇ ⋅ v ) ∇ ⋅ [ ( ∇ v ) T ] = ∇ ⋅ ( v j , i e i ⊗ e j ) = v j , i i e i ⋅ e i ⊗ e j = ∇ 2 v j e j = ∇ 2 v {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)&={\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]&={\boldsymbol {\nabla }}\cdot \left(v_{j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}
Последнее уравнение эквивалентно альтернативному определению/интерпретации [4]
( ∇ ⋅ ) alt ( ∇ v ) = ( ∇ ⋅ ) alt ( v i , j e i ⊗ e j ) = v i , j j e i ⊗ e j ⋅ e j = ∇ 2 v i e i = ∇ 2 v {\displaystyle {\begin{aligned}\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left({\boldsymbol {\nabla }}\mathbf {v} \right)=\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,jj}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\cdot \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{i}~\mathbf {e} _{i}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}
В криволинейных координатах расходимости векторного поля v и тензорного поля второго порядка S {\displaystyle {\boldsymbol {S}}} ∇ ⋅ v = ( ∂ v i ∂ ξ i + v k Γ i k i ) ∇ ⋅ S = ( ∂ S i k ∂ ξ i − S l k Γ i i l − S i l Γ i k l ) g k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &=\left({\cfrac {\partial v^{i}}{\partial \xi ^{i}}}+v^{k}~\Gamma _{ik}^{i}\right)\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left({\cfrac {\partial S_{ik}}{\partial \xi _{i}}}-S_{lk}~\Gamma _{ii}^{l}-S_{il}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{k}\end{aligned}}}
В более общем смысле, ∇ ⋅ S = [ ∂ S i j ∂ q k − Γ k i l S l j − Γ k j l S i l ] g i k b j = [ ∂ S i j ∂ q i + Γ i l i S l j + Γ i l j S i l ] b j = [ ∂ S j i ∂ q i + Γ i l i S j l − Γ i j l S l i ] b j = [ ∂ S i j ∂ q k − Γ i k l S l j + Γ k l j S i l ] g i k b j {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left[{\cfrac {\partial S_{ij}}{\partial q^{k}}}-\Gamma _{ki}^{l}~S_{lj}-\Gamma _{kj}^{l}~S_{il}\right]~g^{ik}~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S^{ij}}{\partial q^{i}}}+\Gamma _{il}^{i}~S^{lj}+\Gamma _{il}^{j}~S^{il}\right]~\mathbf {b} _{j}\\[8pt]&=\left[{\cfrac {\partial S_{~j}^{i}}{\partial q^{i}}}+\Gamma _{il}^{i}~S_{~j}^{l}-\Gamma _{ij}^{l}~S_{~l}^{i}\right]~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S_{i}^{~j}}{\partial q^{k}}}-\Gamma _{ik}^{l}~S_{l}^{~j}+\Gamma _{kl}^{j}~S_{i}^{~l}\right]~g^{ik}~\mathbf {b} _{j}\end{aligned}}}
В цилиндрических полярных координатах ∇ ⋅ v = ∂ v r ∂ r + 1 r ( ∂ v θ ∂ θ + v r ) + ∂ v z ∂ z ∇ ⋅ S = ∂ S r r ∂ r e r + ∂ S r θ ∂ r e θ + ∂ S r z ∂ r e z + 1 r [ ∂ S θ r ∂ θ + ( S r r − S θ θ ) ] e r + 1 r [ ∂ S θ θ ∂ θ + ( S r θ + S θ r ) ] e θ + 1 r [ ∂ S θ z ∂ θ + S r z ] e z + ∂ S z r ∂ z e r + ∂ S z θ ∂ z e θ + ∂ S z z ∂ z e z {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad &{\frac {\partial v_{r}}{\partial r}}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}&{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}&{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}
Ротор тензорного поля порядка n > 1 T ( x ) {\displaystyle {\boldsymbol {T}}(\mathbf {x} )} ( ∇ × T ) ⋅ c = ∇ × ( c ⋅ T ) ; ( ∇ × v ) ⋅ c = ∇ ⋅ ( v × c ) {\displaystyle ({\boldsymbol {\nabla }}\times {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\times (\mathbf {c} \cdot {\boldsymbol {T}})~;\qquad ({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )} c — произвольный постоянный вектор, а v — векторное поле.
[ редактировать ] Рассмотрим векторное поле v и произвольный постоянный вектор c . В индексных обозначениях векторное произведение определяется выражением v × c = ε i j k v j c k e i {\displaystyle \mathbf {v} \times \mathbf {c} =\varepsilon _{ijk}~v_{j}~c_{k}~\mathbf {e} _{i}} ε i j k {\displaystyle \varepsilon _{ijk}} символ перестановки , также известный как символ Леви-Чивита. Затем, ∇ ⋅ ( v × c ) = ε i j k v j , i c k = ( ε i j k v j , i e k ) ⋅ c = ( ∇ × v ) ⋅ c {\displaystyle {\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )=\varepsilon _{ijk}~v_{j,i}~c_{k}=(\varepsilon _{ijk}~v_{j,i}~\mathbf {e} _{k})\cdot \mathbf {c} =({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} } ∇ × v = ε i j k v j , i e k {\displaystyle {\boldsymbol {\nabla }}\times \mathbf {v} =\varepsilon _{ijk}~v_{j,i}~\mathbf {e} _{k}}
Для тензора второго порядка S {\displaystyle {\boldsymbol {S}}} c ⋅ S = c m S m j e j {\displaystyle \mathbf {c} \cdot {\boldsymbol {S}}=c_{m}~S_{mj}~\mathbf {e} _{j}} ∇ × ( c ⋅ S ) = ε i j k c m S m j , i e k = ( ε i j k S m j , i e k ⊗ e m ) ⋅ c = ( ∇ × S ) ⋅ c {\displaystyle {\boldsymbol {\nabla }}\times (\mathbf {c} \cdot {\boldsymbol {S}})=\varepsilon _{ijk}~c_{m}~S_{mj,i}~\mathbf {e} _{k}=(\varepsilon _{ijk}~S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e} _{m})\cdot \mathbf {c} =({\boldsymbol {\nabla }}\times {\boldsymbol {S}})\cdot \mathbf {c} } ∇ × S = ε i j k S m j , i e k ⊗ e m {\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {S}}=\varepsilon _{ijk}~S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e} _{m}}
Наиболее часто используемое тождество, связанное с ротором тензорного поля, T {\displaystyle {\boldsymbol {T}}} ∇ × ( ∇ T ) = 0 {\displaystyle {\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}{\boldsymbol {T}})={\boldsymbol {0}}} S {\displaystyle {\boldsymbol {S}}} ∇ × ( ∇ S ) = 0 ⟹ S m i , j − S m j , i = 0 {\displaystyle {\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}{\boldsymbol {S}})={\boldsymbol {0}}\quad \implies \quad S_{mi,j}-S_{mj,i}=0}
Производная определителя тензора второго порядка [ редактировать ] Производная определителя тензора второго порядка A {\displaystyle {\boldsymbol {A}}} ∂ ∂ A det ( A ) = det ( A ) [ A − 1 ] T . {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}
В ортонормированном базисе компоненты A {\displaystyle {\boldsymbol {A}}} A. можно записать в виде В этом случае правая часть соответствует кофакторам матрицы.
Производные инвариантов тензора второго порядка [ редактировать ] Главные инварианты тензора второго порядка: I 1 ( A ) = tr A I 2 ( A ) = 1 2 [ ( tr A ) 2 − tr A 2 ] I 3 ( A ) = det ( A ) {\displaystyle {\begin{aligned}I_{1}({\boldsymbol {A}})&={\text{tr}}{\boldsymbol {A}}\\I_{2}({\boldsymbol {A}})&={\frac {1}{2}}\left[({\text{tr}}{\boldsymbol {A}})^{2}-{\text{tr}}{{\boldsymbol {A}}^{2}}\right]\\I_{3}({\boldsymbol {A}})&=\det({\boldsymbol {A}})\end{aligned}}}
Производные этих трех инвариантов относительно A {\displaystyle {\boldsymbol {A}}} ∂ I 1 ∂ A = 1 ∂ I 2 ∂ A = I 1 1 − A T ∂ I 3 ∂ A = det ( A ) [ A − 1 ] T = I 2 1 − A T ( I 1 1 − A T ) = ( A 2 − I 1 A + I 2 1 ) T {\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\[3pt]{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}
Доказательство Из производной определителя мы знаем, что ∂ I 3 ∂ A = det ( A ) [ A − 1 ] T . {\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}
Для производных двух других инвариантов вернемся к характеристическому уравнению det ( λ 1 + A ) = λ 3 + I 1 ( A ) λ 2 + I 2 ( A ) λ + I 3 ( A ) . {\displaystyle \det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})~.}
Используя тот же подход, что и для определителя тензора, мы можем показать, что ∂ ∂ A det ( λ 1 + A ) = det ( λ 1 + A ) [ ( λ 1 + A ) − 1 ] T . {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}~.}
Теперь левую часть можно расширить как ∂ ∂ A det ( λ 1 + A ) = ∂ ∂ A [ λ 3 + I 1 ( A ) λ 2 + I 2 ( A ) λ + I 3 ( A ) ] = ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A . {\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\&={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{aligned}}}
Следовательно ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A = det ( λ 1 + A ) [ ( λ 1 + A ) − 1 ] T {\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}} ( λ 1 + A ) T ⋅ [ ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A ] = det ( λ 1 + A ) 1 . {\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\boldsymbol {\mathit {1}}}~.}
Раскрыв правую часть и разделив члены левой части, получим ( λ 1 + A T ) ⋅ [ ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A ] = [ λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 {\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}}
или, [ ∂ I 1 ∂ A λ 3 + ∂ I 2 ∂ A λ 2 + ∂ I 3 ∂ A λ ] 1 + A T ⋅ ∂ I 1 ∂ A λ 2 + A T ⋅ ∂ I 2 ∂ A λ + A T ⋅ ∂ I 3 ∂ A = [ λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 . {\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}
Если мы определим I 0 := 1 {\displaystyle I_{0}:=1} I 4 := 0 {\displaystyle I_{4}:=0} [ ∂ I 1 ∂ A λ 3 + ∂ I 2 ∂ A λ 2 + ∂ I 3 ∂ A λ + ∂ I 4 ∂ A ] 1 + A T ⋅ ∂ I 0 ∂ A λ 3 + A T ⋅ ∂ I 1 ∂ A λ 2 + A T ⋅ ∂ I 2 ∂ A λ + A T ⋅ ∂ I 3 ∂ A = [ I 0 λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 . {\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[I_{0}~\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}
Собирая члены, содержащие различные степени λ, получаем λ 3 ( I 0 1 − ∂ I 1 ∂ A 1 − A T ⋅ ∂ I 0 ∂ A ) + λ 2 ( I 1 1 − ∂ I 2 ∂ A 1 − A T ⋅ ∂ I 1 ∂ A ) + λ ( I 2 1 − ∂ I 3 ∂ A 1 − A T ⋅ ∂ I 2 ∂ A ) + ( I 3 1 − ∂ I 4 ∂ A 1 − A T ⋅ ∂ I 3 ∂ A ) = 0 . {\displaystyle {\begin{aligned}\lambda ^{3}&\left(I_{0}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}\right)+\lambda ^{2}\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}\right)+\\&\qquad \qquad \lambda \left(I_{2}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}\right)+\left(I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right)=0~.\end{aligned}}}
Тогда, ссылаясь на произвольность λ, имеем I 0 1 − ∂ I 1 ∂ A 1 − A T ⋅ ∂ I 0 ∂ A = 0 I 1 1 − ∂ I 2 ∂ A 1 − I 2 1 − ∂ I 3 ∂ A 1 − A T ⋅ ∂ I 2 ∂ A = 0 I 3 1 − ∂ I 4 ∂ A 1 − A T ⋅ ∂ I 3 ∂ A = 0 . {\displaystyle {\begin{aligned}I_{0}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}&=0\\I_{1}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-I_{2}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=0\\I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=0~.\end{aligned}}}
Это означает, что ∂ I 1 ∂ A = 1 ∂ I 2 ∂ A = I 1 1 − A T ∂ I 3 ∂ A = I 2 1 − A T ( I 1 1 − A T ) = ( A 2 − I 1 A + I 2 1 ) T {\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}
Производная тождественного тензора второго порядка [ редактировать ] Позволять 1 {\displaystyle {\boldsymbol {\mathit {1}}}} A {\displaystyle {\boldsymbol {A}}} ∂ 1 ∂ A : T = 0 : T = 0 {\displaystyle {\frac {\partial {\boldsymbol {\mathit {1}}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathsf {0}}}:{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}} 1 {\displaystyle {\boldsymbol {\mathit {1}}}} A {\displaystyle {\boldsymbol {A}}}
Производная тензора второго порядка относительно самого себя [ редактировать ] Позволять A {\displaystyle {\boldsymbol {A}}} ∂ A ∂ A : T = [ ∂ ∂ α ( A + α T ) ] α = 0 = T = I : T {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}
Поэтому, ∂ A ∂ A = I {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathsf {I}}}}
Здесь I {\displaystyle {\boldsymbol {\mathsf {I}}}} I = δ i k δ j l e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}=\delta _{ik}~\delta _{jl}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Этот результат означает, что ∂ A T ∂ A : T = I T : T = T T {\displaystyle {\frac {\partial {\boldsymbol {A}}^{\textsf {T}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}^{\textsf {T}}:{\boldsymbol {T}}={\boldsymbol {T}}^{\textsf {T}}} I T = δ j k δ i l e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}^{\textsf {T}}=\delta _{jk}~\delta _{il}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Следовательно, если тензор A {\displaystyle {\boldsymbol {A}}} ∂ A ∂ A = I ( s ) = 1 2 ( I + I T ) {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~\left({\boldsymbol {\mathsf {I}}}+{\boldsymbol {\mathsf {I}}}^{\textsf {T}}\right)} I ( s ) = 1 2 ( δ i k δ j l + δ i l δ j k ) e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~(\delta _{ik}~\delta _{jl}+\delta _{il}~\delta _{jk})~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Позволять A {\displaystyle {\boldsymbol {A}}} T {\displaystyle {\boldsymbol {T}}} ∂ ∂ A ( A − 1 ) : T = − A − 1 ⋅ T ⋅ A − 1 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\cdot {\boldsymbol {A}}^{-1}} ∂ A i j − 1 ∂ A k l T k l = − A i k − 1 T k l A l j − 1 ⟹ ∂ A i j − 1 ∂ A k l = − A i k − 1 A l j − 1 {\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{ik}^{-1}~T_{kl}~A_{lj}^{-1}\implies {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-A_{ik}^{-1}~A_{lj}^{-1}} ∂ ∂ A ( A − T ) : T = − A − T ⋅ T T ⋅ A − T {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-{\textsf {T}}}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-{\textsf {T}}}\cdot {\boldsymbol {T}}^{\textsf {T}}\cdot {\boldsymbol {A}}^{-{\textsf {T}}}} ∂ A j i − 1 ∂ A k l T k l = − A j k − 1 T l k A l i − 1 ⟹ ∂ A j i − 1 ∂ A k l = − A l i − 1 A j k − 1 {\displaystyle {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{jk}^{-1}~T_{lk}~A_{li}^{-1}\implies {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}=-A_{li}^{-1}~A_{jk}^{-1}} A {\displaystyle {\boldsymbol {A}}} ∂ A i j − 1 ∂ A k l = − 1 2 ( A i k − 1 A j l − 1 + A i l − 1 A j k − 1 ) {\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-{\cfrac {1}{2}}\left(A_{ik}^{-1}~A_{jl}^{-1}+A_{il}^{-1}~A_{jk}^{-1}\right)}
Доказательство Напомним, что ∂ 1 ∂ A : T = 0 {\displaystyle {\frac {\partial {\boldsymbol {\mathit {1}}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}}
С A − 1 ⋅ A = 1 {\displaystyle {\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}={\boldsymbol {\mathit {1}}}} ∂ ∂ A ( A − 1 ⋅ A ) : T = 0 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}\right):{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}}
Использование правила произведения для тензоров второго порядка ∂ ∂ S [ F 1 ( S ) ⋅ F 2 ( S ) ] : T = ( ∂ F 1 ∂ S : T ) ⋅ F 2 + F 1 ⋅ ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial }{\partial {\boldsymbol {S}}}}[{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})]:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}+{\boldsymbol {F}}_{1}\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
мы получаем ∂ ∂ A ( A − 1 ⋅ A ) : T = ( ∂ A − 1 ∂ A : T ) ⋅ A + A − 1 ⋅ ( ∂ A ∂ A : T ) = 0 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}):{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}+{\boldsymbol {A}}^{-1}\cdot \left({\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)={\boldsymbol {\mathit {0}}}} ( ∂ A − 1 ∂ A : T ) ⋅ A = − A − 1 ⋅ T {\displaystyle \left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}}
Поэтому, ∂ ∂ A ( A − 1 ) : T = − A − 1 ⋅ T ⋅ A − 1 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\cdot {\boldsymbol {A}}^{-1}}
Домен Ω {\displaystyle \Omega } Γ {\displaystyle \Gamma } n {\displaystyle \mathbf {n} } Другая важная операция, связанная с тензорными производными в механике сплошных сред, — интегрирование по частям. Формулу интегрирования по частям можно записать в виде ∫ Ω F ⊗ ∇ G d Ω = ∫ Γ n ⊗ ( F ⊗ G ) d Γ − ∫ Ω G ⊗ ∇ F d Ω {\displaystyle \int _{\Omega }{\boldsymbol {F}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {G}}\,d\Omega =\int _{\Gamma }\mathbf {n} \otimes ({\boldsymbol {F}}\otimes {\boldsymbol {G}})\,d\Gamma -\int _{\Omega }{\boldsymbol {G}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {F}}\,d\Omega }
где F {\displaystyle {\boldsymbol {F}}} G {\displaystyle {\boldsymbol {G}}} n {\displaystyle \mathbf {n} } ⊗ {\displaystyle \otimes } ∇ {\displaystyle {\boldsymbol {\nabla }}} F {\displaystyle {\boldsymbol {F}}} теорему о расходимости ∫ Ω ∇ G d Ω = ∫ Γ n ⊗ G d Γ . {\displaystyle \int _{\Omega }{\boldsymbol {\nabla }}{\boldsymbol {G}}\,d\Omega =\int _{\Gamma }\mathbf {n} \otimes {\boldsymbol {G}}\,d\Gamma \,.}
Мы можем выразить формулу интегрирования по частям в декартовых индексных обозначениях как ∫ Ω F i j k . . . . G l m n . . . , p d Ω = ∫ Γ n p F i j k . . . G l m n . . . d Γ − ∫ Ω G l m n . . . F i j k . . . , p d Ω . {\displaystyle \int _{\Omega }F_{ijk....}\,G_{lmn...,p}\,d\Omega =\int _{\Gamma }n_{p}\,F_{ijk...}\,G_{lmn...}\,d\Gamma -\int _{\Omega }G_{lmn...}\,F_{ijk...,p}\,d\Omega \,.}
В особом случае, когда операция тензорного произведения представляет собой сокращение одного индекса, а операция градиента представляет собой расхождение, и обе F {\displaystyle {\boldsymbol {F}}} G {\displaystyle {\boldsymbol {G}}} ∫ Ω F ⋅ ( ∇ ⋅ G ) d Ω = ∫ Γ n ⋅ ( G ⋅ F T ) d Γ − ∫ Ω ( ∇ F ) : G T d Ω . {\displaystyle \int _{\Omega }{\boldsymbol {F}}\cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {G}})\,d\Omega =\int _{\Gamma }\mathbf {n} \cdot \left({\boldsymbol {G}}\cdot {\boldsymbol {F}}^{\textsf {T}}\right)\,d\Gamma -\int _{\Omega }({\boldsymbol {\nabla }}{\boldsymbol {F}}):{\boldsymbol {G}}^{\textsf {T}}\,d\Omega \,.}
В индексной записи ∫ Ω F i j G p j , p d Ω = ∫ Γ n p F i j G p j d Γ − ∫ Ω G p j F i j , p d Ω . {\displaystyle \int _{\Omega }F_{ij}\,G_{pj,p}\,d\Omega =\int _{\Gamma }n_{p}\,F_{ij}\,G_{pj}\,d\Gamma -\int _{\Omega }G_{pj}\,F_{ij,p}\,d\Omega \,.}
^ Дж. К. Симо и Т. Дж. Р. Хьюз, 1998, Вычислительная неэластичность , Springer ^ Дж. Э. Марсден и Т. Дж. Р. Хьюз, 2000, Математические основы эластичности , Дувр. ^ Р.В. Огден, 2000, Нелинейные упругие деформации , Дувр. ^ Перейти обратно: а б Хьельмстад, Кейт (2004). Основы строительной механики . Springer Science & Business Media. п. 45. ИСБН 9780387233307 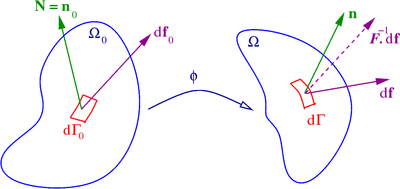
![{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v})[\mathbf {u} ]=\left[{\ frac {d}{d\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/308eadd1b18b96a60ef33e8df365bccc97f0faea)






![{\displaystyle {\frac {\partial \mathbf {f} {\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v})[\mathbf { u} ]=\left[{\frac {d}{d\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0 }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8835d592f0ae810b9b57fa81f345a4850f1f1ce)









![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}: {\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}} ]=\left[{\frac {d}{d\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3916392ebeebca9ebddb31e76edb1c9f8c08b586)







![{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~ {\boldsymbol {T}})\right]_ {\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2072ee23ca460f6f32851f397b5879a47033c3b)
















![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot \mathbf {c} &=\left.{\cfrac {d}{d\alpha }}~{ \boldsymbol {T}}(x_{1}+\alpha c_{1},x_{2}+\alpha c_{2},x_{3}+\alpha c_{3})\right|_{\alpha =0}\equiv \left.{\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(y_{1},y_{2},y_{3})\right|_{\ альфа =0}\\&=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{1}}}~{\cfrac {\partial y_{1}}{\partial \ альфа }}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{2}}}~{\cfrac {\partial y_{2}}{\partial \alpha }}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{3}}}~{\cfrac {\partial y_{3}}{\partial \alpha }}\right]_{\alpha =0}= \left[{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{1}}}~c_{1}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_ {2}}}~c_{2}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{3}}}~c_{3}\right]_{\alpha =0}\ \&={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{1}}}~c_{1}+{\cfrac {\partial {\boldsymbol {T}}}{\partial x_ {2}}}~c_{2}+{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{3}}}~c_{3}\equiv {\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}~c_{i}={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}~(\mathbf {e} _{i}\cdot \mathbf {c} )=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}\otimes \mathbf {e} _{i} \right]\cdot \mathbf {c} \qquad \square \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b848452c7189fb099eb1dadf20cd7c167dd4d2e)








![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi = {}\quad & {\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r} +{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi } \partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} ={}\quad &{\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\times \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{r}}{ \partial \theta }}-v_{\theta }\right)~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{r}}{ \partial z}}~\mathbf {e} _{r}\times \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{\theta }}{\partial r }}~\mathbf {e} _{\theta }\times \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }} {\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\times \mathbf {e} _{\theta }+{\frac {\partial v_{\theta } }{\partial z}}~\mathbf {e} _{\theta }\times \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{z}}{\ частичный r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{z}\times \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\times \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad &{\frac {\partial S_{rr}}{ \partial r}}~\mathbf {e} _{r}\times \mathbf {e} _{r}\times \mathbf {e} _{r}+{\frac {\partial S_{rr}}{ \partial z}}~\mathbf {e} _{r}\times \mathbf {e} _{r}\times \mathbf {e} _{z}+{\frac {1}{r}}\left [{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\times \mathbf {e} _{r}\times \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{r\theta }}{\partial r}}~\ mathbf {e} _{r}\times \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial z} }~\mathbf {e} _{r}\times \mathbf {e} _{\theta }\times \mathbf {e} _{z}+{\frac {1}{r}}\left[{\ frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\times \mathbf {e} _{\theta }\times \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e } _{r}\times \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e } _{r}\times \mathbf {e} _{z}\times \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rz }}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\ theta }\\{}+{}&{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\times \mathbf {e} _{r }\times \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\times \mathbf {e} _{r}\times \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+ (S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\times \mathbf {e} _{\ theta }\times \mathbf {e} _{r}+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\times \mathbf { e} _{\theta }\times \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta }}{\partial \ theta } }+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\times \mathbf {e} _{\theta }\times \mathbf { e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\times \mathbf {e} _{z}\times \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\times \mathbf {e} _{z}\times \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{} +{ }&{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\times \mathbf {e} _{r}\times \mathbf {e} _ {r }+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\times \mathbf {e} _{r}\times \mathbf {e} _ {z }+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e } _ {z}\times \mathbf {e} _{r}\times \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{z\theta }}{ \partial r}}~\mathbf {e} _{z}\times \mathbf {e} _{\theta }\times \mathbf {e} _{r}+{\frac {\partial S_{z\theta }} {\partial z}}~\mathbf {e} _{z}\times \mathbf {e} _{\theta }\times \mathbf {e} _{z}+{\frac {1}{r }} \left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\times \mathbf {e} _{ \theta }\times \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{ z} \otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{ z} \otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\times \mathbf {e} _{z}\times \mathbf {e} _{\theta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f19df7af85562767daf41dcce9042d343a7cf917)








![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)&= {\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\times \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i} \cdot \mathbf {e} _{i}\times \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~ \mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\ cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]&= {\boldsymbol {\nabla }}\cdot \left(v_ {j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\times \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~\mathbf {e} _{j}={\boldsymbol { \nabla }}^{2}\mathbf {v} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864380cd0a82178354a80ee58109fc0519c149ba)


![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left[{\cfrac {\partial S_{ij}}{\partial q^{k} }}-\Gamma _{ki}^{l}~S_{lj}-\Gamma _{kj}^{l}~S_{il}\right]~g^{ik}~\mathbf {b} ^ {j}\\[8pt]&=\left[{\cfrac {\partial S^{ij}}{\partial q^{i}}}+\Gamma _{il}^{i}~S^{ lj}+\Gamma _{il}^{j}~S^{il}\right]~\mathbf {b} _{j}\\[8pt]&=\left[{\cfrac {\partial S_{ ~j}^{i}}{\partial q^{i}}}+\Gamma _{il}^{i}~S_{~j}^{l}-\Gamma _{ij}^{l} ~S_{~l}^{i}\right]~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S_{i}^{~j}}{ \partial q^{k}}}-\Gamma _{ik}^{l}~S_{l}^{~j}+\Gamma _{kl}^{j}~S_{i}^{~l }\right]~g^{ik}~\mathbf {b} _{j}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85fad1b0228d189867b87f1d770c3968e4394860)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad &{\frac {\partial v_{r}}{\partial r}}+{\frac { 1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\ частичный z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}&{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac { \partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\ frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\ \{}+{}&{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\ частичный z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8cd23836a8e6cc12150592c3964d95d6a3f94e9)











![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{ \boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a229cf1ec76d8d0d6c4ebf0e55e24a9289524d0f)

![{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}&=\left.{\cfrac {d}{d \alpha }}\det({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right|_{\alpha =0}\\&=\left.{\cfrac {d}{ d\alpha }}\det \left[\alpha ~{\boldsymbol {A}}\left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I}}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_{\alpha =0}\\&=\left.{\cfrac {d}{d\ альфа }}\left[\alpha ^{3}~\det({\boldsymbol {A}})~\det \left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I }}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_ {\alpha =0}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a280dfed26c159c4b698ac9db1c9e7b4ff9ce7c)


![{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}&=\left.{\cfrac {d}{d \alpha }}\left[\alpha ^{3}~\det({\boldsymbol {A}})~\left({\cfrac {1}{\alpha ^{3}}}+I_{1}\ left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~{\cfrac {1}{\alpha ^{2}}}+I_{2}\left( {\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~{\cfrac {1}{\alpha }}+I_{3}\left({\boldsymbol {A} }^{-1}\cdot {\boldsymbol {T}}\right)\right)\right]\right|_{\alpha =0}\\&=\left.\det({\boldsymbol {A} })~{\cfrac {d}{d\alpha }}\left[1+I_{1}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right )~\alpha +I_{2}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{2}+I_{3}\left ({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{3}\right]\right|_{\alpha =0}\\&=\ left.\det({\boldsymbol {A}})~\left[I_{1}({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}})+2~I_{2 }\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha +3~I_{3}\left({\boldsymbol {A}}^{ -1}\cdot {\boldsymbol {T}}\right)~\alpha ^{2}\right]\right|_{\alpha =0}\\&=\det({\boldsymbol {A}}) ~I_{1}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc69b4584b67f7559a984e1c3d5dfa5b0f663c83)


![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {A}}}}: {\boldsymbol {T}}=\det({\boldsymbol {A}})~{\text{tr} }\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)=\det({\boldsymbol {A}})~\left[{\boldsymbol {A} }^{-1}\right]^{\textsf {T}}:{\boldsymbol {T}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcfbbc8e843ee49828711668186ed4e5faa93384)
![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1 }\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf1328c61318cc48aa33f6c0b580b55e268f7ebe)
![{\displaystyle {\begin{aligned}I_{1}({\boldsymbol {A}})&={\text{tr}}{\boldsymbol {A}}\\I_{2}({\boldsymbol {A }})&={\frac {1}{2}}\left[({\text{tr}}{\boldsymbol {A}})^{2}-{\text{tr}}{{\boldsymbol {A}}^{2}}\right]\\I_{3}({\boldsymbol {A}})&=\det({\boldsymbol {A}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5f440de0bb33a949001c6bef13f9f829fb1a42)
![{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\[3pt] {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^ {\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~\ left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}} ^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left ({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf { Т}}\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19cf1ad5bce9774bf510c8818f4b90e32c4f2640)
![{\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^ {-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9dd4a16751516c5e316be643e40ce0babf1c1df)

![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\ det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A }})^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be1b29969a25190e4efad41db9d76f11e8a8079)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol { A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\ лямбда ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\&={\frac {\partial I_ {1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4ad226ea72ae236eaddfe419007ff6de53d55d)
![{\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\ жирный символ {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1} }}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\ тексты {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3993a79ec1f95da1b9e188243300861ee7ee2e45)
![{\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1} }{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\ frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}} )~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/782fb846f7870890e72cda9dbeba6e80dfc064b0)
![{\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\ лямбда +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2} +I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d9d08c98dc866bcc330678342ca3c391da0042a)
![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+ {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A }}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}} {\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\ частичный {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A }}}}\\&=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\ матит {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6174aae82fa111cbe2235a21c275bb7bc0e243b4)


![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+ {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A }}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {\mathit {1}}}+{\boldsymbol { A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A} }^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^ {\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T} }\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[I_{0}~\lambda ^{3}+I_{1}~ \lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8169e3ea8470a718a349e0d8a73e1fb7c162914)





![{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}: {\boldsymbol {T}}=\left[{\frac {\partial }{\ частичный \alpha }}({\boldsymbol {A}}+\alpha ~ {\boldsymbol {T}})\right]_ {\alpha =0}= {\boldsymbol {T}}= {\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4cf9341eabbe69c48f4ff85db571b84c8b2c318)















![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {S}}}}[{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F }}_{2}({\boldsymbol {S}})]:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial { \boldsymbol {S}}}}: {\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}+{\boldsymbol {F}}_{1}\cdot \left({ \frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a25e5e0ee3f8a2f287da104d5f72d8342899b9)













