ириса Набор данных о цветке
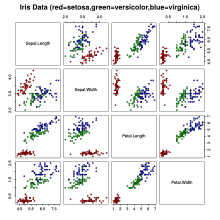
Набор ириса данных цветка или Фишера ириса набор данных — это многомерный набор данных , используемый и ставший известным британским статистиком и биологом Рональдом Фишером в его статье 1936 года «Использование множественных измерений в таксономических задачах как пример линейного дискриминантного анализа» . [1] Его иногда называют Андерсона ирисов набором данных , потому что Эдгар Андерсон собрал данные для количественной оценки морфологических вариаций цветков ирисов трех родственных видов. [2] Два из трех видов были собраны на полуострове Гаспе «все с одного и того же пастбища, собраны в один и тот же день и измерены в одно и то же время одним и тем же человеком с помощью одного и того же прибора». [3]
Набор данных состоит из 50 образцов каждого из трех видов ириса ( Iris setosa , Iris Virginica и Iris versicolor ). У каждого образца измеряли четыре признака : длину и ширину чашелистиков и лепестков в сантиметрах. Основываясь на сочетании этих четырех особенностей, Фишер разработал линейную дискриминантную модель, позволяющую отличать виды друг от друга. Статья Фишера была опубликована в « Анналах евгеники» (сегодня « Анналы генетики человека »). [1]
Использование набора данных [ править ]


Фишера Первоначально использовавшийся в качестве примера набора данных, к которому был применен линейный дискриминантный анализ , он стал типичным тестовым примером для многих статистической классификации методов в машинном обучении, таких как машины опорных векторов . [5]
Однако использование этого набора данных в кластерном анализе не является распространенным, поскольку набор данных содержит только два кластера с довольно очевидным разделением. Один из кластеров содержит Iris setosa , а другой кластер содержит как Iris Virginica , так и Iris versicolor , и его невозможно отделить без информации о видах, которую использовал Фишер. Это делает набор данных хорошим примером для объяснения разницы между контролируемыми и неконтролируемыми методами интеллектуального анализа данных : линейную дискриминантную модель Фишера можно получить только тогда, когда известны виды объектов: метки классов и кластеры не обязательно совпадают. [6]
Тем не менее, все три вида Iris разделимы в проекции на нелинейную и ветвящуюся главную компоненту. [7] Набор данных аппроксимируется ближайшим деревом с некоторым штрафом за чрезмерное количество узлов, изгиб и растяжение. Затем строится так называемая «карта метро». [4] Точки данных проецируются в ближайший узел. Для каждого узла составляется круговая диаграмма прогнозируемых точек. Площадь круга пропорциональна количеству прогнозируемых точек. Из диаграммы (слева) видно, что абсолютное большинство образцов разных видов ирисов принадлежит разным узлам. Лишь небольшая часть Iris-virginica смешана с Iris-versicolor (смешанные сине-зеленые узлы на диаграмме). Таким образом, три вида ириса ( Iris setosa , Iris Virginica и Iris versicolor ) можно разделить с помощью неконтролируемых процедур нелинейного анализа главных компонент . Чтобы их различить, достаточно просто выбрать соответствующие узлы на главном дереве.
Набор данных [ изменить ]

Набор данных содержит набор из 150 записей по пяти атрибутам: длина чашелистика, ширина чашелистика, длина лепестка, ширина лепестка и вид.



Набор данных радужной оболочки глаза широко используется в качестве набора данных для начинающих в целях машинного обучения. Набор данных включен в R базу и Python в библиотеку машинного обучения scikit-learn , поэтому пользователи могут получить к нему доступ без необходимости искать для него источник.
Было опубликовано несколько версий набора данных. [8]
Код R , иллюстрирующий использование [ править ]
Пример кода R, показанный ниже, воспроизводит диаграмму рассеяния, показанную в начале этой статьи:
# Show the dataset
iris
# Show the help page, with information about the dataset
?iris
# Create scatterplots of all pairwise combination of the 4 variables in the dataset
pairs(iris[1:4], main="Iris Data (red=setosa,green=versicolor,blue=virginica)",
pch=21, bg=c("red","green3","blue")[unclass(iris$Species)])
Код Python , иллюстрирующий использование [ править ]
from sklearn.datasets import load_iris
iris = load_iris()
iris
Этот код дает:
{'data': array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3., 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],...
'target': array([0, 0, 0, ... 1, 1, 1, ... 2, 2, 2, ...
'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),
...}
См. также [ править ]
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б Р. А. Фишер (1936). «Использование множественных измерений в таксономических задачах». Анналы евгеники . 7 (2): 179–188. дои : 10.1111/j.1469-1809.1936.tb02137.x . hdl : 2440/15227 .
- ^ Эдгар Андерсон (1936). «Проблема видов в Iris » . Анналы ботанического сада Миссури . 23 (3): 457–509. дои : 10.2307/2394164 . JSTOR 2394164 .
- ^ Эдгар Андерсон (1935). «Ирисы полуострова Гаспе». Бюллетень Американского общества ирисов . 59 : 2–5.
- ↑ Перейти обратно: Перейти обратно: а б А. Н. Горбань , А. Зиновьев. Основные многообразия и графы на практике: от молекулярной биологии к динамическим системам , Международный журнал нейронных систем, Vol. 20, № 3 (2010) 219–232.
- ^ «Репозиторий машинного обучения UCI: набор данных Iris» . archive.ics.uci.edu . Проверено 1 декабря 2017 г.
- ^ Инес Фербер; Стефан Гюннеманн; Ханс-Петер Кригель ; Пер Крёгер; Эммануэль Мюллер; Эрих Шуберт; Томас Зайдль; Артур Зимек (2010). «Об использовании меток классов при оценке кластеризации» (PDF) . В Сяоли З. Ферн; Ян Дэвидсон; Дженнифер Дай (ред.). MultiClust: обнаружение, обобщение и использование нескольких кластеров . АСМ СИГКДД .
- ^ А. Н. Горбань, Н. Р. Самнер и А. Я. Зиновьев, Топологические грамматики для аппроксимации данных , Письма по прикладной математике, том 20, выпуск 4 (2007), 382-386.
- ^ Бездек, Дж. К.; Келлер, Дж. М.; Кришнапурам, Р.; Кунчева Л.И. ; Пал, НР (1999). «Поддержите ли вы настоящие данные по радужной оболочке?». Транзакции IEEE в нечетких системах . 7 (3): 368–369. дои : 10.1109/91.771092 .
Seliyana [ edit ]
- «Данные Фишера об ирисе» . (Содержит две задокументированные ошибки) . Репозиторий машинного обучения UCI: набор данных Iris.