График рассеяния

График рассеяния
График рассеяния
Один из семи основных инструментов качества
Впервые описан	Джон Гершель
Цель	Определить тип связи (если таковая имеется) между двумя количественными переменными.

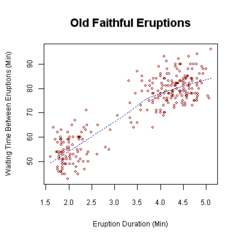
Время ожидания между извержениями и продолжительность извержения гейзера Old Faithful в Йеллоустонском национальном парке , штат Вайоминг , США. На этой диаграмме показано, что обычно существует два типа извержений: кратковременные и кратковременные и длительные и продолжительные.

Диаграмма рассеяния , также называемая диаграммой рассеяния , диаграммой рассеяния , диаграммой рассеяния , диаграммой рассеяния или диаграммой рассеяния , ^[2] — это тип графика или математической диаграммы, использующий декартовы координаты для отображения значений обычно двух переменных для набора данных. Если точки закодированы (цвет/форма/размер), может отображаться одна дополнительная переменная.Данные отображаются в виде набора точек, каждая из которых имеет значение одной переменной, определяющей положение на горизонтальной оси, и значение другой переменной, определяющей положение на вертикальной оси . ^[3]

Первое описание диаграммы рассеяния обычно приписывают Джону Гершелю (1792–1871). ^[4]^[5]

Обзор

Диаграмму рассеяния можно использовать либо в том случае, когда одна непрерывная переменная находится под контролем экспериментатора, а другая зависит от нее, либо когда обе непрерывные переменные независимы. Если существует параметр , который систематически увеличивается и/или уменьшается за счет другого, он называется параметром управления или независимой переменной и обычно отображается по горизонтальной оси. Измеряемая или зависимая переменная обычно отображается вдоль вертикальной оси. Если зависимой переменной не существует, любой тип переменной может быть нанесен на любую ось, а диаграмма рассеяния будет иллюстрировать только степень корреляции (не причинно-следственную связь ) между двумя переменными. ^{[ нужна ссылка ]}

Диаграмма рассеяния может указывать на различные виды корреляций между переменными с определенным доверительным интервалом . Например, вес и рост будут находиться на $оси Y$ , а рост — на $X.$ оси Корреляции могут быть положительными (растущими), отрицательными (падающими) или нулевыми (некоррелированными). Если рисунок точек имеет наклон от нижнего левого угла к верхнему правому, это указывает на положительную корреляцию между изучаемыми переменными. Если рисунок точек имеет наклон от верхнего левого угла к нижнему правому, это указывает на отрицательную корреляцию. Линия наилучшего соответствия (также называемая «линией тренда») может быть проведена для изучения взаимосвязи между переменными. Уравнение корреляции между переменными можно определить с помощью установленных процедур наилучшего соответствия. Для линейной корреляции наиболее подходящая процедура известна как линейная регрессия и гарантированно генерирует правильное решение за конечное время. Никакая универсальная процедура наилучшего соответствия не может гарантировать правильное решение для произвольных отношений. Диаграмма рассеяния также очень полезна, когда мы хотим увидеть, как два сопоставимых набора данных согласуются, чтобы показать нелинейные связи между переменными. Возможность сделать это можно улучшить, добавив плавную линию, например ЛЕСС . ^[6] Более того, если данные представлены в виде смешанной модели простых отношений, эти отношения будут визуально очевидны как наложенные шаблоны. ^{[ нужна ссылка ]}

Диаграмма разброса — один из семи основных инструментов контроля качества . ^[7]

Точечные диаграммы могут быть построены в виде пузырьковых , маркерных и/или линейных диаграмм . ^[8]

Пример

Например, чтобы продемонстрировать связь между емкостью легких человека и тем, как долго этот человек может задерживать дыхание, исследователь должен выбрать группу людей для изучения, затем измерить емкость легких каждого из них (первая переменная) и то, как долго этот человек сможет задерживать дыхание. задержать дыхание (вторая переменная). Затем исследователь наносил данные на диаграмму рассеяния, откладывая «объем легких» по горизонтальной оси и «время задержки дыхания» по вертикальной оси. ^{[ нужна ссылка ]}

Человек с объемом легких 400 кл , задержавший дыхание на 21,7 с , будет представлен на диаграмме рассеяния одной точкой в точке (400, 21,7) в декартовых координатах . Диаграмма рассеяния всех людей, участвовавших в исследовании, позволит исследователю получить визуальное сравнение двух переменных в наборе данных и поможет определить, какой тип взаимосвязи может существовать между двумя переменными. ^{[ нужна ссылка ]}

Матрицы точечной диаграммы

Для набора переменных данных (размерностей) X ₁ , X ₂ , ... , X _k матрица точечной диаграммы показывает все попарные диаграммы рассеяния переменных в одном представлении с несколькими диаграммами рассеяния в матричном формате. Для $k$ переменных матрица диаграммы рассеяния будет содержать $k$ строк и $k$ столбцов. График, расположенный на пересечении строки и $j$ -го столбца, представляет собой график переменных X _i в сравнении с X _j . ^[9] Это означает, что каждая строка и столбец имеют одно измерение, а каждая ячейка отображает диаграмму рассеяния в двух измерениях. ^{[ нужна ссылка ]}

Обобщенная матрица диаграммы рассеяния ^[10] предлагает ряд отображений парных комбинаций категориальных и количественных переменных. , Мозаичный график диаграмма колебаний или фасетная гистограмма могут использоваться для отображения двух категориальных переменных. Остальные графики используются для одной категориальной и одной количественной переменных.

См. также

Ссылки

^ Визуализации, созданные с помощью VisIt на сайте wci.llnl.gov. Последнее обновление: 8 ноября 2007 г.
^ Джаррелл, Стивен Б. (1994). Базовая статистика (Специальное предварительное издание). Дубьюк, Айова: Wm. Паб C. Brown. п. 492. ИСБН 978-0-697-21595-6 . Когда мы ищем взаимосвязь между двумя количественными переменными, часто помогает стандартный график доступных пар данных (X,Y), называемый диаграммой разброса ...
^ Уттс, Джессика М. Видя статистику насквозь, 3-е издание, Томсон Брукс/Коул, 2005, стр. 166-167. ISBN 0-534-39402-7
^ Дружелюбный, Майкл; Денис, Дэн (2005). «Раннее возникновение и развитие диаграммы рассеяния». Журнал истории поведенческих наук . 41 (2): 103–130. дои : 10.1002/jhbs.20078 . ПМИД 15812820 .
^ https://www.datavis.ca/papers/Friendly-scat.pdf
^ Кливленд, Уильям (1993). Визуализация данных . Мюррей Хилл, Саммит Нью-Джерси, Нью-Джерси: At & T Bell Laboratories, опубликовано Hobart Press. ISBN 978-0963488404 .
^ Нэнси Р. Тейг (2004). «Семь основных инструментов качества» . Набор инструментов качества . Милуоки, Висконсин : Американское общество качества . п. 15 . Проверено 5 февраля 2010 г.
^ «Точечная диаграмма – Документация по диаграммам AnyChart JavaScript» . AnyChart. Архивировано из оригинала 1 февраля 2016 года . Проверено 3 февраля 2016 г.
^ Матрица точечной диаграммы на сайте itl.nist.gov.
^ Эмерсон, Джон В.; Грин, Уолтон А.; Шерке, Баррет; Кроули, Джейсон (2013). «Обобщенный парный сюжет». Журнал вычислительной и графической статистики . 22 (1): 79–91. дои : 10.1080/10618600.2012.694762 . S2CID 28344569 .

Дальнейшее чтение

Каттанео, Матиас Д.; Крамп, Ричард К.; Фаррелл, Макс Х.; Фэн, Инцзе (2024). « О Бинскаттере ». Американский экономический обзор . 114 (5): 1488–1514.

Внешние ссылки

СМИ, связанные с диаграммами рассеяния, на Викискладе?
Что такое диаграмма рассеяния? Архивировано 7 августа 2020 г. в Wayback Machine.
Матрица корреляционной диаграммы рассеяния для упорядоченно-категориальных данных . Пояснение и R-код.
Диаграмма рассеяния плотности для больших наборов данных (сотни миллионов точек)

[1] Визуализации, созданные с помощью VisIt на сайте wci.llnl.gov. Последнее обновление: 8 ноября 2007 г.

[2] Джаррелл, Стивен Б. (1994). Базовая статистика (Специальное предварительное издание). Дубьюк, Айова: Wm. Паб C. Brown. п. 492. ИСБН 978-0-697-21595-6 . Когда мы ищем взаимосвязь между двумя количественными переменными, часто помогает стандартный график доступных пар данных (X,Y), называемый диаграммой разброса ...

[3] Уттс, Джессика М. Видя статистику насквозь, 3-е издание, Томсон Брукс/Коул, 2005, стр. 166-167. ISBN 0-534-39402-7

[4] Дружелюбный, Майкл; Денис, Дэн (2005). «Раннее возникновение и развитие диаграммы рассеяния». Журнал истории поведенческих наук . 41 (2): 103–130. дои : 10.1002/jhbs.20078 . ПМИД 15812820 .

[5] ttps://www.datavis.ca/papers/Friendly-scat.pdf

[6] Кливленд, Уильям (1993). Визуализация данных . Мюррей Хилл, Саммит Нью-Джерси, Нью-Джерси: At & T Bell Laboratories, опубликовано Hobart Press. ISBN 978-0963488404 .

[7] Нэнси Р. Тейг (2004). «Семь основных инструментов качества» . Набор инструментов качества . Милуоки, Висконсин : Американское общество качества . п. 15 . Проверено 5 февраля 2010 г.

[8] «Точечная диаграмма – Документация по диаграммам AnyChart JavaScript» . AnyChart. Архивировано из оригинала 1 февраля 2016 года . Проверено 3 февраля 2016 г.

[9] Матрица точечной диаграммы на сайте itl.nist.gov.

[10] Эмерсон, Джон В.; Грин, Уолтон А.; Шерке, Баррет; Кроули, Джейсон (2013). «Обобщенный парный сюжет». Журнал вычислительной и графической статистики . 22 (1): 79–91. дои : 10.1080/10618600.2012.694762 . S2CID 28344569 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]