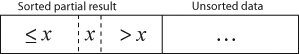Сортировка вставкой
 Анимация сортировки вставкой | |
| Сорт | Алгоритм сортировки |
|---|---|
| Структура данных | Множество |
| Худшая производительность | сравнения и обмены |
| Лучшая производительность | сравнения, свопы |
| Средняя производительность | сравнения и обмены |
| Наихудшая пространственная сложность | общий, вспомогательный |
| Оптимальный | Нет |
Сортировка вставками — это простой алгоритм сортировки , который создает окончательный отсортированный массив (или список) по одному элементу за раз путем сравнения . Для больших списков он гораздо менее эффективен, чем более продвинутые алгоритмы, такие как быстрая сортировка , пирамидальная сортировка или сортировка слиянием . Однако сортировка вставками дает несколько преимуществ:
- Простая реализация: Джон Бентли показывает трехстрочную версию C / C++ составляет пять строк , которая при оптимизации . [1]
- Эффективен для (довольно) небольших наборов данных, как и другие квадратичные числа (т. е. O ( n 2 )) алгоритмы сортировки
- На практике более эффективен, чем большинство других простых квадратичных алгоритмов, таких как сортировка выбором или пузырьковая сортировка.
- Адаптивный , то есть эффективный для наборов данных, которые уже существенно отсортированы: временная сложность равна O ( kn ), когда каждый элемент на входе находится не более чем на k позициях от своей отсортированной позиции.
- Стабильный ; т.е. не меняет относительный порядок элементов с одинаковыми ключами
- На месте ; т. е. требуется только постоянный объем O (1) дополнительного пространства памяти.
- Онлайн ; т. е. может сортировать список по мере его получения
Когда люди вручную сортируют карты в бриджевой раздаче, большинство из них используют метод, похожий на сортировку вставками. [2]
Алгоритм
[ редактировать ]
Сортировка вставкой выполняет итерацию , потребляя один входной элемент при каждом повторении, и увеличивает отсортированный выходной список. На каждой итерации сортировка вставкой удаляет один элемент из входных данных, находит место, которому он принадлежит, в отсортированном списке и вставляет его туда. Это повторяется до тех пор, пока не останется ни одного входного элемента.
Сортировка обычно выполняется на месте, путем итерации массива и увеличения отсортированного списка за ним. В каждой позиции массива он сравнивает это значение с наибольшим значением в отсортированном списке (которое оказывается рядом с ним в предыдущей проверенной позиции массива). Если больше, он оставляет элемент на месте и переходит к следующему. Если меньше, он находит правильную позицию в отсортированном списке, сдвигает все большие значения вверх, чтобы освободить место, и вставляет в эту правильную позицию.
Результирующий массив после k итераций имеет свойство сортировки первых k + 1 записей («+1», потому что первая запись пропускается). На каждой итерации первая оставшаяся запись входных данных удаляется и вставляется в результат в правильной позиции, расширяя таким образом результат:
становится
при этом каждый элемент больше x копируется вправо при сравнении с x .
Самый распространенный вариант сортировки вставками, работающий с массивами, можно описать следующим образом:
- Предположим, существует функция Insert, предназначенная для вставки значения в отсортированную последовательность в начале массива. Он начинается с конца последовательности и сдвигает каждый элемент на одну позицию вправо до тех пор, пока не будет найдено подходящее положение для нового элемента. Функция имеет побочный эффект: перезаписывает значение, хранящееся сразу после отсортированной последовательности в массиве.
- Чтобы выполнить сортировку вставкой, начните с самого левого элемента массива и вызовите Insert, чтобы вставить каждый встреченный элемент в его правильную позицию. Упорядоченная последовательность, в которую вставляется элемент, сохраняется в начале массива в уже рассмотренном наборе индексов. Каждая вставка перезаписывает одно значение: вставляемое значение.
Далее следует псевдокод полного алгоритма, где массивы начинаются с нуля : [1]
i ← 1
while i < length(A)
j ← i
while j > 0 and A[j-1] > A[j]
swap A[j] and A[j-1]
j ← j - 1
end while
i ← i + 1
end while
Внешний цикл проходит по всем элементам, кроме первого, поскольку префикс одного элемента A[0:1] сортируется тривиально, поэтому инвариант, заключающийся в том, что первый i записи сортируются верно с самого начала. Внутренний цикл перемещает элемент A[i] на свое правильное место, чтобы после цикла первый i+1 элементы сортируются. Обратите внимание, что and-оператор в тесте должен использовать короткую оценку , иначе тест может привести к ошибке границ массива , когда j=0 и он пытается оценить A[j-1] > A[j] (т.е. доступ к A[-1] терпит неудачу).
После расширения swap операция на месте, как x ← A[j]; A[j] ← A[j-1]; A[j-1] ← x (где x является временной переменной), можно создать немного более быструю версию, которая перемещается A[i] на свою позицию за один раз и выполняет только одно присваивание во внутреннем теле цикла: [1]
i ← 1
while i < length(A)
x ← A[i]
j ← i
while j > 0 and A[j-1] > x
A[j] ← A[j-1]
j ← j - 1
end while
A[j] ← x[3]
i ← i + 1
end while
Новый внутренний цикл сдвигает элементы вправо, освобождая место для x = A[i].
Алгоритм также может быть реализован рекурсивным способом. Рекурсия просто заменяет внешний цикл, вызывая себя и сохраняя последовательно меньшие значения n в стеке до тех пор, пока n не станет равным 0, после чего функция затем возвращается вверх по цепочке вызовов для выполнения кода после каждого рекурсивного вызова, начиная с n, равного 1, с n увеличивается на 1, когда каждый экземпляр функции возвращается к предыдущему экземпляру. Первоначальный вызов будет InsertionSortR(A, length(A)-1) .
function insertionSortR(array A, int n)
if n > 0
insertionSortR(A, n-1)
x ← A[n]
j ← n-1
while j >= 0 and A[j] > x
A[j+1] ← A[j]
j ← j-1
end while
A[j+1] ← x
end if
end function
Это не делает код короче, но и не уменьшает время выполнения, но увеличивает дополнительное потребление памяти с O(1) до O(N) (на самом глубоком уровне рекурсии стек содержит N ссылок на A массив, каждый из которых имеет соответствующее значение переменной n от N до 1).
Лучший, худший и средний случаи
[ редактировать ]В лучшем случае входными данными является уже отсортированный массив. В этом случае сортировка вставками имеет линейное время выполнения (т. е. O( n )). Во время каждой итерации первый оставшийся элемент входных данных сравнивается только с самым правым элементом отсортированного подраздела массива.
Простейший входной сигнал в худшем случае — это массив, отсортированный в обратном порядке. Набор всех входных данных для наихудшего случая состоит из всех массивов, где каждый элемент является наименьшим или вторым по величине из элементов перед ним. В этих случаях каждая итерация внутреннего цикла будет сканировать и сдвигать весь отсортированный подраздел массива перед вставкой следующего элемента. Это дает сортировке вставками квадратичное время выполнения (т. е. O( n 2 )).
Средний случай также является квадратичным, [4] что делает сортировку вставками непрактичной для сортировки больших массивов. Однако сортировка вставками — один из самых быстрых алгоритмов сортировки очень маленьких массивов, даже быстрее, чем быстрая сортировка ; действительно, хорошие реализации быстрой сортировки используют сортировку вставкой для массивов, меньших определенного порога, даже когда они возникают как подзадачи; точный порог должен быть определен экспериментально и зависит от машины, но обычно составляет около десяти.
Пример: В следующей таблице показаны шаги сортировки последовательности {3, 7, 4, 9, 5, 2, 6, 1}. На каждом этапе подчеркивается рассматриваемый ключ. Ключ, который был перемещен (или оставлен на месте, поскольку он был самым большим из рассмотренных) на предыдущем шаге, отмечен звездочкой.
3 7 4 9 5 2 6 1 3* 7 4 9 5 2 6 1 3 7* 4 9 5 2 6 1 3 4* 7 9 5 2 6 1 3 4 7 9* 5 2 6 1 3 4 5* 7 9 2 6 1 2* 3 4 5 7 9 6 1 2 3 4 5 6* 7 9 1 1* 2 3 4 5 6 7 9
Связь с другими алгоритмами сортировки
[ редактировать ]Сортировка вставкой очень похожа на сортировку выбором . Как и при сортировке выбором, после прохождения k через массив первые k элементов располагаются в отсортированном порядке. Однако фундаментальное различие между этими двумя алгоритмами заключается в том, что сортировка вставкой сканирует назад от текущего ключа, а сортировка выбором — вперед. В результате при сортировке выбором первые k элементов становятся k наименьшими элементами несортированных входных данных, а при сортировке вставками они являются просто первыми k элементами входных данных.
Основное преимущество сортировки вставкой перед сортировкой выбором состоит в том, что сортировка выбором всегда должна сканировать все оставшиеся элементы, чтобы найти самый маленький элемент в неотсортированной части списка, тогда как сортировка вставкой требует только одного сравнения, когда ( k + 1)-st элемент больше k -го элемента; когда это часто так (например, если входной массив уже отсортирован или частично отсортирован), сортировка вставкой явно более эффективна по сравнению с сортировкой выбором. В среднем (при условии, что ранг ( k + 1)-го элемента является случайным), сортировка вставкой потребует сравнения и сдвига половины предыдущих k элементов, а это означает, что сортировка вставкой будет выполнять примерно вдвое меньше сравнений, чем сортировка выбором. средний.
В худшем случае сортировки вставкой (когда входной массив подвергается обратной сортировке) сортировка вставкой выполняет столько же сравнений, сколько и сортировка выбором. Однако недостатком сортировки вставкой по сравнению с сортировкой выбором является то, что она требует большего количества операций записи, поскольку на каждой итерации вставка ( k + 1)-го элемента в отсортированную часть массива требует множества перестановок элементов для смещения всех элементов. следующих элементов, тогда как для каждой итерации сортировки выбором требуется только одна замена. В общем случае сортировка вставками записывает данные в массив O( n 2 ) раз, тогда как сортировка выбором будет записывать только O( n ) раз. По этой причине сортировка выбором может быть предпочтительнее в тех случаях, когда запись в память значительно дороже, чем чтение, например, в EEPROM или флэш-памяти .
В то время как некоторые алгоритмы «разделяй и властвуй», такие как быстрая сортировка и сортировка слиянием, превосходят сортировку вставкой для больших массивов, нерекурсивные алгоритмы сортировки, такие как сортировка вставкой или сортировка выбором, обычно работают быстрее для очень маленьких массивов (точный размер зависит от среды и реализации, но обычно составляет от 7 до 50 элементов). Следовательно, полезной оптимизацией при реализации этих алгоритмов является гибридный подход, использующий более простой алгоритм, когда массив разделен на небольшой размер. [1]
Варианты
[ редактировать ]DL Shell внесла существенные улучшения в алгоритм; модифицированная версия называется сортировкой Шелла . Алгоритм сортировки сравнивает элементы, разделенные расстоянием, которое уменьшается с каждым проходом. Сортировка Шелла значительно улучшила время выполнения в практической работе: два простых варианта требуют O( n 3/2 ) и O( n 4/3 ) время работы. [5] [6]
Если стоимость сравнений превышает стоимость свопов, как, например, в случае со строковыми ключами, хранящимися по ссылке или при взаимодействии с человеком (например, при выборе одного из пары, отображаемой рядом), то использование двоичной сортировки вставкой может дать результат лучшая производительность. [7] Двоичная сортировка вставкой использует двоичный поиск для определения правильного места для вставки новых элементов и, следовательно, ⌈log 2 n в худшем случае выполняет сравнения ⌉. Когда каждый элемент в массиве ищется и вставляется, это O( n log n ). [7] Алгоритм в целом по-прежнему имеет время работы O( n 2 ) в среднем из-за серии свопов, необходимых для каждой вставки. [7]
Количество перестановок можно уменьшить, вычислив положение нескольких элементов перед их перемещением. Например, если целевая позиция двух элементов вычисляется до того, как они будут перемещены в правильное положение, количество перестановок может быть уменьшено примерно на 25% для случайных данных. В крайнем случае этот вариант работает аналогично сортировке слиянием .
Вариант под названием «Двоичная сортировка слиянием» использует двоичную сортировку вставкой для сортировки групп из 32 элементов, за которой следует окончательная сортировка с использованием сортировки слиянием . Он сочетает в себе скорость сортировки вставкой для небольших наборов данных со скоростью сортировки слиянием для больших наборов данных. [8]
Чтобы избежать необходимости делать серию замен для каждой вставки, входные данные могут храниться в связанном списке , что позволяет включать элементы в список или из него за постоянное время, когда позиция в списке известна. Однако поиск в связанном списке требует последовательного перехода по ссылкам к нужной позиции: связанный список не имеет произвольного доступа, поэтому в нем нельзя использовать более быстрый метод, например бинарный поиск. Следовательно, время выполнения поиска равно O( n ), а время сортировки — O( n 2 ). более сложная структура данных (например, куча или двоичное дерево Если используется ), время, необходимое для поиска и вставки, может быть значительно сокращено; в этом суть сортировки кучи и сортировки двоичного дерева .
В 2006 году Бендер, Мартин Фарах-Колтон и Мостейро опубликовали новый вариант сортировки вставками, названный библиотечной сортировкой или сортировкой вставкой с промежутками , который оставляет небольшое количество неиспользуемых пробелов (то есть «пробелов»), разбросанных по всему массиву. Преимущество состоит в том, что вставкам нужно только сдвигать элементы до тех пор, пока не будет достигнут пробел. Авторы показывают, что этот алгоритм сортировки работает с высокой вероятностью за время O( n log n ). [9]
Если используется список пропуска , время вставки сокращается до O(log n ), и замены не требуются, поскольку список пропуска реализован в структуре связанного списка. Окончательное время выполнения вставки будет равно O( n log n ).
Список кодов сортировки вставкой в C
[ редактировать ]Если элементы хранятся в связанном списке, то список можно отсортировать с дополнительным пространством O (1). Алгоритм начинается с изначально пустого (и, следовательно, тривиально отсортированного) списка. Входные элементы удаляются из списка по одному, а затем вставляются в нужное место в отсортированном списке. Когда входной список пуст, отсортированный список имеет желаемый результат.
struct LIST * SortList1(struct LIST * pList)
{
// zero or one element in list
if (pList == NULL || pList->pNext == NULL)
return pList;
// head is the first element of resulting sorted list
struct LIST * head = NULL;
while (pList != NULL) {
struct LIST * current = pList;
pList = pList->pNext;
if (head == NULL || current->iValue < head->iValue) {
// insert into the head of the sorted list
// or as the first element into an empty sorted list
current->pNext = head;
head = current;
} else {
// insert current element into proper position in non-empty sorted list
struct LIST * p = head;
while (p != NULL) {
if (p->pNext == NULL || // last element of the sorted list
current->iValue < p->pNext->iValue) // middle of the list
{
// insert into middle of the sorted list or as the last element
current->pNext = p->pNext;
p->pNext = current;
break; // done
}
p = p->pNext;
}
}
}
return head;
}
В приведенном ниже алгоритме используется конечный указатель. [10] для вставки в отсортированный список. Более простой рекурсивный метод каждый раз перестраивает список (вместо объединения) и может использовать O( n стековое пространство ).
struct LIST
{
struct LIST * pNext;
int iValue;
};
struct LIST * SortList(struct LIST * pList)
{
// zero or one element in list
if (!pList || !pList->pNext)
return pList;
/* build up the sorted array from the empty list */
struct LIST * pSorted = NULL;
/* take items off the input list one by one until empty */
while (pList != NULL) {
/* remember the head */
struct LIST * pHead = pList;
/* trailing pointer for efficient splice */
struct LIST ** ppTrail = &pSorted;
/* pop head off list */
pList = pList->pNext;
/* splice head into sorted list at proper place */
while (!(*ppTrail == NULL || pHead->iValue < (*ppTrail)->iValue)) { /* does head belong here? */
/* no - continue down the list */
ppTrail = &(*ppTrail)->pNext;
}
pHead->pNext = *ppTrail;
*ppTrail = pHead;
}
return pSorted;
}
Ссылки
[ редактировать ]- ↑ Перейти обратно: Перейти обратно: а б с д Бентли, Джон (2000). «Столбец 11: Сортировка» . Жемчуг программирования (2-е изд.). ACM Press / Эддисон-Уэсли. стр. 115–116. ISBN 978-0-201-65788-3 . OCLC 1047840657 .
- ^ Седжвик, Роберт (1983). Алгоритмы . Аддисон-Уэсли. п. 95. ИСБН 978-0-201-06672-2 .
- ^ Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009) [1990], «Раздел 2.1: Сортировка вставками», Введение в алгоритмы (3-е изд.), MIT Press и McGraw-Hill, стр. 16–18, ISBN 0-262-03384-4 . См., в частности, стр. 18.
- ^ Шварц, Кейт. «Почему в среднем случае сортировка вставкой Θ(n^2)? (ответ «templatetypedef»)» . Переполнение стека.
- ^ Фрэнк, РМ; Лазарь, РБ (1960). «Процедура высокоскоростной сортировки» . Коммуникации АКМ . 3 (1): 20–22. дои : 10.1145/366947.366957 . S2CID 34066017 .
- ^ Седжвик, Роберт (1986). «Новая верхняя граница сортировки Шелл». Журнал алгоритмов . 7 (2): 159–173. дои : 10.1016/0196-6774(86)90001-5 .
- ↑ Перейти обратно: Перейти обратно: а б с Саманта, Дебасис (2008). Классические структуры данных . Обучение PHI. п. 549. ИСБН 9788120337312 .
- ^ «Двоичная сортировка слиянием»
- ^ Бендер, Майкл А.; Фарах-Колтон, Мартин ; Мостейро, Мигель А. (2006), «Сортировка вставкой равна O ( n log n )», Theory of Computing Systems , 39 (3): 391–397, arXiv : cs/0407003 , doi : 10.1007/s00224-005-1237 -z , MR 2218409 , S2CID 14701669
- ^ Хилл, Курт (редактор), «Техника следящего указателя», Эйлер , Государственный университет Вэлли-Сити, заархивировано из оригинала 26 апреля 2012 года , получено 22 сентября 2012 года .
Дальнейшее чтение
[ редактировать ]- Кнут, Дональд (1998), «5.2.1: Сортировка вставкой», Искусство компьютерного программирования , том. 3. Сортировка и поиск (второе изд.), Аддисон-Уэсли, стр. 80–105, ISBN. 0-201-89685-0 .
Внешние ссылки
[ редактировать ]- Анимированные алгоритмы сортировки: сортировка вставками в Wayback Machine (архивировано 8 марта 2015 г.) - графическая демонстрация
- Адамовский, Джон Пол, Сортировка двоичными вставками – Табло – Полное исследование и реализация на языке C , Pathcom .
- Сортировка вставками – сравнение с другими сортировками O(n 2 ) Алгоритмы сортировки , Великобритания : Core war .
- Сортировка вставками (C) (вики), LiteratePrograms - реализации сортировки вставками на C и некоторых других языках программирования.