Основная теорема о гомоморфизмах

В абстрактной алгебре фундаментальная теорема о гомоморфизмах , также известная как фундаментальная теорема о гомоморфизме или первая теорема об изоморфизме , связывает структуру двух объектов, между которыми гомоморфизм задан , а также ядра и образа гомоморфизма.

Теорема о гомоморфизме используется для доказательства теорем об изоморфизме .

-

Схема основной теоремы о гомоморфизмах, где f — гомоморфизм, N — нормальная подгруппа группы G а e — единичный элемент группы G. ,

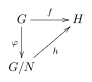
Для данных двух групп G и H и группового гомоморфизма f : G → H пусть N — нормальная подгруппа в G , а φ — естественный сюръективный гомоморфизм G → G / N (где G / N — факторгруппа группы G по N ). Если N — подмножество ker ) , ( f то существует единственный гомоморфизм h : G / N → H такой, что f = h ∘ φ .

Другими словами, естественная проекция φ универсальна , среди гомоморфизмов на G которые отображают N в единичный элемент .

Ситуацию описывает следующая коммутативная диаграмма :

h инъективен тогда и только тогда, когда N = ker( f ) . Поэтому, полагая N = ker( f ) , мы сразу получаем первую теорему об изоморфизме .

Утверждение основной теоремы о гомоморфизмах групп можно записать так: «Каждый гомоморфный образ группы изоморфен факторгруппе ».

Доказательство

Доказательство следует из двух основных фактов о гомоморфизмах, а именно из сохранения групповой операции и отображения единичного элемента в единичный элемент. Нам нужно показать, что если $\phi :G\to H$ является гомоморфизмом групп, то:

1. ${\text{im}}(\phi )$ is a subgroup of является подгруппой $H$‍ .
2. $G/\ker(\phi )$ is isomorphic to изоморфен ${\text{im}}(\phi )$‍ .

Доказательство 1

Операция, которая сохраняется $\phi$ is the group operation. If это групповая операция. Если $a,b\in {\text{im}}(\phi )$, то существуют элементы , then there exist elements $a',b'\in G$ такой, что $\phi (a')=a$ and и $\phi (b')=b$. Для этих . For these $a$ and и $b$у нас есть , we have $ab=\phi (a')\phi (b')=\phi (a'b')\in {\text{im}}(\phi )$ (с $\phi$ preserves the group operation), and thus, the closure property is satisfied in сохраняет групповую операцию), и, таким образом, свойство замыкания выполняется в ${\text{im}}(\phi )$. Элемент идентификации . The identity element $e\in H$ также находится в ${\text{im}}(\phi )$ потому что $\phi$ отображает идентификационный элемент $G$ к этому. Поскольку каждый элемент $a'$ в $G$ имеет обратную $(a')^{-1}$ такой, что $\phi ((a')^{-1})=(\phi (a'))^{-1}$ (потому что $\phi$ сохраняет и обратное свойство), мы имеем обратный для каждого элемента $\phi (a')=a$ in в ${\text{im}}(\phi )$поэтому , , therefore, ${\text{im}}(\phi )$ is a subgroup of  является подгруппой $H$‍ .

Доказательство 2

Построить карту $\psi :G/\ker(\phi )\to {\text{im}}(\phi )$ by к $\psi (a\ker(\phi ))=\phi (a)$. . This map is well-defined, as if Эта карта четко определена, как будто $a\ker(\phi )=b\ker(\phi )$‍затем $b^{-1}a\in \ker(\phi )$ и так $\phi (b^{-1}a)=e\Rightarrow \phi (b^{-1})\phi (a)=e$ which gives что дает $\phi (a)=\phi (b)$. Это отображение является изоморфизмом. . This map is an isomorphism. $\psi$ является сюръективным на ${\text{im}}(\phi )$ по определению. Чтобы показать инъективность, если $\psi (a\ker(\phi ))=\psi (b\ker(\phi ))$, then , затем $\phi (a)=\phi (b)$, что подразумевает , which implies $b^{-1}a\in \ker(\phi )$ so так $a\ker(\phi )=b\ker(\phi )$. Окончательно, . Finally,$$\psi ((a\ker(\phi ))(b\ker(\phi )))=\psi (ab\ker(\phi ))=\phi (ab)=\phi (a)\phi (b)=\psi (a\ker(\phi ))\psi (b\ker(\phi )),$$следовательно $\psi$ сохраняет групповую операцию. Следовательно $\psi$ является изоморфизмом между $G/\ker(\phi )$ and и ${\text{im}}(\phi )$, что завершает доказательство. , which completes the proof.

Приложения

Теоретико-групповую версию фундаментальной теоремы о гомоморфизме можно использовать, чтобы показать, что две выбранные группы изоморфны. Два примера показаны ниже.

Целые числа по модулю n

For each Для каждого $n\in \mathbb {N}$, рассмотрим группы , consider the groups $\mathbb {Z}$ и $\mathbb {Z} _{n}$ и групповой гомоморфизм $f:\mathbb {Z} \rightarrow \mathbb {Z} _{n}$ определяется $m\mapsto m{\text{ mod }}n$ (см. модульную арифметику ). Далее рассмотрим ядро $f$‍ , ‍ ${\text{ker}}(f)=n\mathbb {Z}$, , which is a normal subgroup in которая является нормальной подгруппой в $\mathbb {Z}$. Существует естественный сюръективный гомоморфизм . There exists a natural surjective homomorphism $\varphi :\mathbb {Z} \rightarrow \mathbb {Z} /n\mathbb {Z}$ defined by определяется $m\mapsto m+n\mathbb {Z}$. Теорема утверждает, что существует изоморфизм . The theorem asserts that there exists an isomorphism $h$ между $\mathbb {Z} _{n}$ and и $\mathbb {Z} /n\mathbb {Z}$или , or in other words другими словами $\mathbb {Z} _{n}\cong \mathbb {Z} /n\mathbb {Z}$. Коммутативная диаграмма показана ниже. . The commutative diagram is illustrated below.

N / C Теорема

Позволять $G$ быть группой с подгруппой $H$. . Let Позволять $C_{G}(H)$‍ , $N_{G}(H)$ и ${\text{Aut}}(H)$ — централизатор , нормализатор и автоморфизмов группа $H$ in в $G$соответственно , respectively. Then, the . Тогда теорема N / C утверждает, что $N_{G}(H)/C_{G}(H)$ is isomorphic to a subgroup of изоморфна подгруппе ${\text{Aut}}(H)$‍ .

Доказательство

Мы можем найти групповой гомоморфизм $f:N_{G}(H)\rightarrow {\text{Aut}}(H)$ defined by определяется $g\mapsto ghg^{-1}$, , for all для всех $h\in H$. Очевидно, что ядро . Clearly, the kernel of $f$ is является $C_{G}(H)$. Следовательно, мы имеем естественный сюръективный гомоморфизм . Hence, we have a natural surjective homomorphism $\varphi :N_{G}(H)\rightarrow N_{G}(H)/C_{G}(H)$ defined by определяется $g\mapsto gC(H)$. Тогда фундаментальная теорема о гомоморфизме утверждает, что существует изоморфизм между . The fundamental homomorphism theorem then asserts that there exists an isomorphism between $N_{G}(H)/C_{G}(H)$ and и $\varphi (N_{G}(H))$, , which is a subgroup of которая является подгруппой ${\text{Aut}}(H)$‍ .

Другие версии

Аналогичные теоремы справедливы для моноидов , векторных пространств , модулей и колец .

См. также

• Категория фактора

Ссылки

• Бичи, Джон А. (1999), «Теорема 1.2.7 (фундаментальная теорема о гомоморфизме)», Вводные лекции по кольцам и модулям , Студенческие тексты Лондонского математического общества, том. 47, Издательство Кембриджского университета, с. 27, ISBN  9780521644075
• Гроув, Ларри К. (2012), «Теорема 1.11 (Фундаментальная теорема о гомоморфизме)», Алгебра , Dover Books on Mathematics, Courier Corporation, стр. 11, ISBN  9780486142135
• Джейкобсон, Натан (2012), «Фундаментальная теорема о гомоморфизмах Ω-алгебр», Основная алгебра II , Dover Books on Mathematics (2-е изд.), Courier Corporation, стр. 62, ISBN  9780486135212
• Роуз, Джон С. (1994), «3.24 Фундаментальная теорема о гомоморфизмах», Курс теории групп [перепечатка оригинала 1978 года] , Dover Publications, Inc., Нью-Йорк, стр. 44–45, ISBN  0-486-68194-7 , МР   1298629