Атомный электронный переход

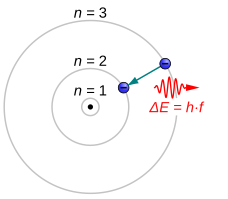
Электрон в атоме модели Бора переходит с квантового уровня $n = 3$ на $n = 2$ и испускает фотон . Энергия электрона определяется его орбитой вокруг атома. Орбита с n = 0, обычно называемая основным состоянием , имеет наименьшую энергию из всех состояний в системе.

В атомной физике и химии переход атомного электрона (также называемый атомным переходом, квантовым скачком или квантовым скачком) — это электрона переход с одного энергетического уровня на другой внутри атома. ^[1] или искусственный атом . ^[2] Временной масштаб квантового скачка экспериментально не измерен. Однако принцип Франка-Кондона связывает верхний предел этого параметра порядком аттосекунд . ^[3]

Электроны, перепрыгивающие на энергетические уровни с меньшим n, испускают электромагнитное излучение в виде фотона. Электроны также могут поглощать проходящие фотоны, что приводит к квантовому скачку на уровень с более высоким n. Чем больше энергетическое разделение между начальным и конечным состоянием электрона, тем короче длина волны фотонов . ^[4]

История

Датский физик Нильс Бор впервые предположил, что электроны могут совершать квантовые скачки, в 1913 году. ^[5] Вскоре после этого Джеймс Франк и Густав Людвиг Герц экспериментально доказали , что атомы имеют квантованные энергетические состояния. ^[6]

Наблюдаемость квантовых скачков была предсказана Гансом Демельтом в 1975 году, а впервые они наблюдались с использованием захваченных ионов бария в 1986 в Гамбургском университете и ртути в НИСТ году. ^[4]

Теория

Атом взаимодействует с осциллирующим электрическим полем:

E(t)=|{\textbf {E}}_{0}|Re(e^{-i{\omega }t}{\hat {\textbf {e}}}_{\mathrm {rad} })

( 1 )

с амплитудой $|{\textbf {E}}_{0}|$ , угловая частота $\omega$ и вектор поляризации ${\hat {\textbf {e}}}_{\mathrm {rad} }$ . ^[7] Обратите внимание, что фактическая фаза $(\omega t-{\textbf {k}}\cdot {\textbf {r}})$ . Однако во многих случаях изменение ${\textbf {k}}\cdot {\textbf {r}}$ мала по размеру атома (или, что то же самое, длина волны излучения намного больше размера атома), и этим членом можно пренебречь. Это называется дипольным приближением. Атом также может взаимодействовать с осциллирующим магнитным полем, создаваемым излучением, хотя и гораздо слабее.

Гамильтониан этого взаимодействия, аналогичный энергии классического диполя в электрическом поле, равен $H_{I}=e{\textbf {r}}\cdot {\textbf {E}}(t)$ . Скорость стимулированного перехода можно рассчитать с помощью теории возмущений, зависящей от времени ; однако результат можно суммировать, используя золотое правило Ферми : $Rate\propto |eE_{0}|^{2}\times |\langle 2|{\textbf {r}}\cdot {\hat {\textbf {e}}}_{\mathrm {rad} }|1\rangle |^{2}$ Дипольный матричный элемент можно разложить на произведение радиального интеграла и углового интеграла. Угловой интеграл равен нулю, если не выполняются правила отбора атомного перехода.

Недавние открытия

было показано В 2019 году в эксперименте со сверхпроводящим искусственным атомом, состоящим из двух сильногибридизированных трансмон-кубитов, помещенных внутри полости считывающего резонатора при температуре 15 мК , , что эволюция некоторых скачков является непрерывной, когерентной, детерминированной и обратимой. ^[8] С другой стороны, другие квантовые скачки по своей сути непредсказуемы. ^[9]

См. также

Ссылки

^ Шомберт, Джеймс. «Квантовая физика» Физический факультет Университета Орегона
^ Виджай, Р; Слихтер, Д.Х; Сиддики, я (2011). «Наблюдение квантовых скачков в сверхпроводящем искусственном атоме». Письма о физических отзывах . 106 (11): 110502. arXiv : 1009.2969 . Бибкод : 2011PhRvL.106k0502V . doi : 10.1103/PhysRevLett.106.110502 . ПМИД 21469850 . S2CID 35070320 .
^ де ла Пенья, Л.; Четто, AM; Вальдес-Эрнандес, А. (4 декабря 2020 г.). «Насколько быстр квантовый скачок?» . Буквы по физике А. 384 (34): 126880. arXiv : 2009.02426 . Бибкод : 2020PhLA..38426880D . doi : 10.1016/j.physleta.2020.126880 . ISSN 0375-9601 .
^ Jump up to: ^а ^б Итано, ВМ; Бергквист, JC; Вайнленд, диджей (2015). «Ранние наблюдения макроскопических квантовых скачков в одиночных атомах» (PDF) . Международный журнал масс-спектрометрии . 377 : 403. Бибкод : 2015IJMSp.377..403I . дои : 10.1016/j.ijms.2014.07.005 .
^ Глейк, Джеймс (21 октября 1986 г.). «ФИЗИКИ НАКОНЕЦ-ТО УВИДЕЛИ КВАНТОВЫЙ Прыжок СОБСТВЕННЫМИ ГЛАЗАМИ» . Нью-Йорк Таймс . ISSN 0362-4331 . Проверено 6 декабря 2021 г.
^ «Эксперимент Франка-Герца | физика | Британника» . www.britanica.com . Проверено 6 декабря 2021 г.
^ Фут, CJ (2004). Атомная физика . Издательство Оксфордского университета. ISBN 978-0-19-850696-6 .
^ Минев З.К.; Мундхада, СО; Шанкар, С.; Рейнхольд, П.; Гутьеррес-Хареги, Р.; Шелькопф, Р.Дж.; Миррахими, М.; Кармайкл, HJ; Деворет, Миннесота (3 июня 2019 г.). «Чтобы поймать и обратить вспять квантовый прыжок в полете». Природа . 570 (7760): 200–204. arXiv : 1803.00545 . Бибкод : 2019Natur.570..200M . дои : 10.1038/s41586-019-1287-z . ПМИД 31160725 . S2CID 3739562 .
^ Снижко Кирилл; Кумар, Парвин; Ромито, Алессандро (29 сентября 2020 г.). «Квантовый эффект Зенона проявляется поэтапно» . Обзор физических исследований . 2 (3): 033512. arXiv : 2003.10476 . Бибкод : 2020PhRvR...2c3512S . doi : 10.1103/PhysRevResearch.2.033512 . S2CID 214623209 .

Внешние ссылки

Шрёдингер, Эрвин (август 1952 г.). «Существуют ли квантовые скачки? Часть I» (PDF) . Британский журнал философии науки . 3 (10): 109–123. дои : 10.1093/bjps/iii.10.109 . Часть 2
«Нет ни квантовых скачков, ни частиц!» Х.Д. Зех, Physics Letters A172 , 189 (1993).
Болл, Филип (5 июня 2019 г.). «Квантовые скачки, которые долгое время считались мгновенными, требуют времени» . Журнал Кванта . Проверено 6 июня 2019 г.
«Поверхностный плазмон на границе раздела металл-диэлектрик с переходным слоем эпсилон-околонулевой» Кевина Роккаприоре и др., Physical Review B 103 , L161404 (2021).

[1] Шомберт, Джеймс. «Квантовая физика» Физический факультет Университета Орегона

[2] Виджай, Р; Слихтер, Д.Х; Сиддики, я (2011). «Наблюдение квантовых скачков в сверхпроводящем искусственном атоме». Письма о физических отзывах . 106 (11): 110502. arXiv : 1009.2969 . Бибкод : 2011PhRvL.106k0502V . doi : 10.1103/PhysRevLett.106.110502 . ПМИД 21469850 . S2CID 35070320 .

[3] де ла Пенья, Л.; Четто, AM; Вальдес-Эрнандес, А. (4 декабря 2020 г.). «Насколько быстр квантовый скачок?» . Буквы по физике А. 384 (34): 126880. arXiv : 2009.02426 . Бибкод : 2020PhLA..38426880D . doi : 10.1016/j.physleta.2020.126880 . ISSN 0375-9601 .

[:0-4] Jump up to: ^а ^б Итано, ВМ; Бергквист, JC; Вайнленд, диджей (2015). «Ранние наблюдения макроскопических квантовых скачков в одиночных атомах» (PDF) . Международный журнал масс-спектрометрии . 377 : 403. Бибкод : 2015IJMSp.377..403I . дои : 10.1016/j.ijms.2014.07.005 .

[5] Глейк, Джеймс (21 октября 1986 г.). «ФИЗИКИ НАКОНЕЦ-ТО УВИДЕЛИ КВАНТОВЫЙ Прыжок СОБСТВЕННЫМИ ГЛАЗАМИ» . Нью-Йорк Таймс . ISSN 0362-4331 . Проверено 6 декабря 2021 г.

[6] «Эксперимент Франка-Герца | физика | Британника» . www.britanica.com . Проверено 6 декабря 2021 г.

[7] Фут, CJ (2004). Атомная физика . Издательство Оксфордского университета. ISBN 978-0-19-850696-6 .

[8] Минев З.К.; Мундхада, СО; Шанкар, С.; Рейнхольд, П.; Гутьеррес-Хареги, Р.; Шелькопф, Р.Дж.; Миррахими, М.; Кармайкл, HJ; Деворет, Миннесота (3 июня 2019 г.). «Чтобы поймать и обратить вспять квантовый прыжок в полете». Природа . 570 (7760): 200–204. arXiv : 1803.00545 . Бибкод : 2019Natur.570..200M . дои : 10.1038/s41586-019-1287-z . ПМИД 31160725 . S2CID 3739562 .

[9] Снижко Кирилл; Кумар, Парвин; Ромито, Алессандро (29 сентября 2020 г.). «Квантовый эффект Зенона проявляется поэтапно» . Обзор физических исследований . 2 (3): 033512. arXiv : 2003.10476 . Бибкод : 2020PhRvR...2c3512S . doi : 10.1103/PhysRevResearch.2.033512 . S2CID 214623209 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]