Лоренц-инвариантность в некритической теории струн
Обычно некритическая теория струн рассматривается в рамках подхода, предложенного Поляковым . [ 1 ] Другой подход был разработан в. [ 2 ] [ 3 ] [ 4 ] Он представляет собой универсальный метод поддержания явной лоренц-инвариантности в любой квантовой релятивистской теории. На примере теории струн Намбу-Гото в 4-мерном пространстве-времени Минковского эту идею можно продемонстрировать следующим образом:


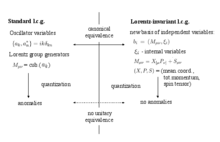
Геометрически мировой лист струны рассечен системой параллельные плоскости для фиксации конкретного параметризация или калибр на нем. Плоскости определяются вектором нормали n μ , калибровочной осью. Если этот вектор принадлежит световому конусу , то параметризация соответствует для освещения калибра конуса , если он направлен вдоль мирового листа период P μ , это время похоже на калибровку Рорлиха . Проблема штатного света конусная калибровка заключается в том, что вектор n µ постоянен, например n µ = (1, 1, 0, 0), а система самолетов "заморожена" у Минковского пространство-время. Преобразования Лоренца меняют положение мировой лист относительно этих фиксированных плоскостей, и им следуют путем репараметризации мирового листа. На квантовом уровне Группа репараметризации имеет аномалию , который появляется также в группе Лоренца и нарушает лоренц-инвариантность теории. С другой стороны, Калибровка Рорлиха связывает n μ с самим мировым листом. В результате генераторы Лоренца преобразуют n µ и мировой лист одновременно, без репараметризаций. То же свойство имеет если отнести светоподобную ось n μ с мировым листом, используя в в дополнение к P μ доступны другие динамические векторы в теории струн. Таким образом строится лоренц-инвариантная параметризация мировой лист, где группа Лоренца действует тривиально и не имеют квантовые аномалии.
Алгебраически это соответствует каноническому преобразованию a i -> b i в классической механике к новому набору переменных, явно содержащему все необходимые генераторы симметрий. Для стандартной калибровки светового конуса генераторы Лоренца M µν являются кубическими относительно переменных осциллятора a i , и их квантование приобретает хорошо известную аномалию. Рассмотрим набор b i = (M µν ,ξ i ), который содержит генераторы группы Лоренца и внутренние переменные ξ i , дополняющие M µν в полное фазовое пространство. При выборе такого набора нужно позаботиться о том, чтобы ξ i имели простые скобки Пуассона с M µν и между собой. Локальное существование таких переменных обеспечивается теоремой Дарбу . Квантование в новом наборе переменных устраняет аномалию группы Лоренца. Канонически эквивалентные классические теории не обязательно соответствуют унитарным эквивалентным квантовым теориям, поэтому квантовые аномалии могут присутствовать в одном подходе и отсутствовать в другом.
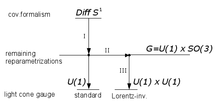
Теоретико-групповой теория струн обладает калибровочной симметрией Diff S 1 , репараметризации окружности. Симметрия создается за счет Алгебра Вирасоро L n . Стандартный датчик светового конуса фиксирует большую часть градусов шкалы. свободы, оставляющей только тривиальные повороты фаз U(1) ~ S 1 . Они соответствуют периодической эволюции струн, порождаемой Гамильтониан L 0 . Давайте добавим дополнительный слой на эту диаграмму: группа G = U(1) x SO(3) калибровочных преобразований мирового листа, включая тривиальный фактор эволюции и повороты калибровочной оси в системе центра масс относительно фиксированного мирового листа. Стандартный датчик светового конуса соответствует выбору одной точки в коэффициенте SO(3), что приводит к Лоренц-неинвариантная параметризация. Поэтому необходимо выбрать другой представитель на калибровочной орбите G, на этот раз связана с мировым листом лоренц-инвариантным образом. После приведения механики к этому представителю из теории исключены аномальные калибровочные степени свободы. Тривиальная калибровочная симметрия U(1) x U(1) сохраняется, включая эволюцию и те вращения, которые сохраняют направление калибровочной оси.
Успешная реализация этой программы осуществлена в г. [ 3 ] [ 4 ] . [ 5 ] Это несколько унитарных неэквивалентных версий квантовая открытая теория струн Намбу-Гото, где калибровочная ось привязан к различным геометрическим особенностям мирового листа. Их общими свойствами являются
- явная лоренц-инвариантность при d=4
- репараметризация степеней свободы, фиксированных калибровкой
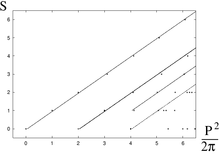
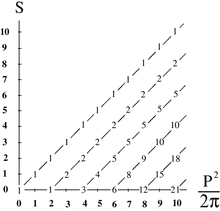
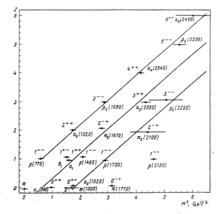
- Редже-подобный спектр спин-масс
Читатель знаком с разнообразием сосуществующих ветвей. в современной теории струн не будет удивляться, почему так много разных квантовых теорий могут быть построены по существу для одной и той же физической системы. Описанный здесь подход не предполагает создание уникальный конечный результат, он просто предоставляет набор инструментов подходит для построения собственной квантовой теории струн. Поскольку можно использовать любое значение размерности, и особенно d=4, приложения могли бы быть более реалистичными. Например, этот подход можно применить в физика адронов , описать их спектры и электромагнитные взаимодействия . [ 6 ] [ 7 ]
Ссылки
[ редактировать ]- ^ Поляков, А.М. (1981). «Квантовая геометрия бозонных струн». Буквы по физике Б. 103 (3). Эльзевир Б.В.: 207–210. дои : 10.1016/0370-2693(81)90743-7 . ISSN 0370-2693 . : в статье показано в рамках формулировки интеграла по путям , что квантовая теория струн Намбу-Гото в d=26 эквивалентно набору линейных осцилляторов, хотя и при других значениях размерности теория существует, и содержит нелинейную теорию поля связанные с модами Лиувилля . Статьи, цитируемые ниже, используются для квантования. Операторный формализм Дирака .
- ^ Рорлих, Ф. (31 марта 1975 г.). «Квантовая динамика релятивистской струны». Письма о физических отзывах . 34 (13). Американское физическое общество (APS): 842–845. дои : 10.1103/physrevlett.34.842 . ISSN 0031-9007 .
- ^ Jump up to: а б с Пронько, ГП (1990). «Гамильтонова теория релятивистской струны». Обзоры по математической физике . 02 (3). World Scientific Pub Co Pte Lt: 355–398. дои : 10.1142/s0129055x90000119 . ISSN 0129-055X .
- ^ Jump up to: а б с Клименко С.В., Никитин И.Н., Некритическая теория струн: классические и квантовые аспекты, Nova Science Pub., Нью-Йорк 2006, ISBN 1-59454-267-8 .
- ^ Jump up to: а б Краткая энциклопедия суперсимметрии и некоммутативные структуры в математике и физике, запись «Подмножества без аномалий», Kluwer Academic Publishers, Дордрехт, 2003 г., ISBN 1-4020-1338-8 .
- ^ Jump up to: а б Бердников Е.Б.; Нанобашвили, Г.Г.; Пронько, врач общей практики (10.06.1993). «Релятивистская теория главных траекторий и электромагнитных переходов легких мезонов, часть I». Международный журнал современной физики А. 08 (14). World Scientific Pub Co Pte Lt: 2447–2464. дои : 10.1142/s0217751x93000965 . ISSN 0217-751X .
- ^ Jump up to: а б Бердников Е.Б.; Нанобашвили, Г.Г.; Пронько, врач общей практики (20 июня 1993 г.). «Релятивистская теория главных траекторий и электромагнитных переходов легких мезонов, часть II». Международный журнал современной физики А. 08 (15). World Scientific Pub Co Pte Lt: 2551–2567. дои : 10.1142/s0217751x93001016 . ISSN 0217-751X .
См. также
[ редактировать ]В следующих учебниках по теории струн упоминается возможность безаномального квантования струны вне критического измерения:
- Л. Бринк, М. Энно, Принципы теории струн, Plenum Press, Нью-Йорк и Лондон, (1988), с. 157
Не следует ли попытаться использовать другое представление
строковых операторов, чтобы избежать центрального обвинения? Опять же, вполне возможно построить такой представление, и если это так, то весьма вероятно, что результирующая квантовая теория будет сильно отличаться от той, которую объяснено здесь. Возможно, это еще не построенное теория будет обладать собственным внутренним интересом (например, за счет возникновения бесконечномерных представления алгебры Лоренца). Более того, потому что эта теория не будет основана на использовании переменные осциллятора, его можно было бы легче расширить к объектам более высоких измерений, таким как мембрана.
Далее, на стр. 157–159, квантовые решения теории замкнутых струн в классе неосцилляторных представлений, не обладающих аномалией в алгебре Вирасоро при произвольном четном значении размерности являются представлен явно.
- Б.М. Барбашов, В.В. Нестеренко, Введение в релятивистскую теорию струн, Сингапур, World Scientific, (1990), с. 64:
Трудно понять, что столь тщательно изученный
объект в классической теории и нерелятивистской квантовой механике поскольку строку невозможно последовательно проанализировать на квантовом уровне в реалистичном 4-мерном пространстве-времени. Были предприняты попытки найти другие квантовые решения проблемы релятивистских струн который не столкнулся бы с вышеперечисленными трудностями.
Далее, в разделах 11 и 30 квантование некритических теория струн в рамках подходов Рорлиха и Полякова описано.
- М. Грин, Дж. Шварц, Э. Виттен, Теория суперструн. Том. 1, Кембриджский университет. Пресс, (1987), с. 124:
учитывая вклад конформного фактора φ в интеграле по путям замечено:
Можно предположить, что интеграл (3.1.13) физически
разумно, даже если зависимость φ не устраняется. Эта возможность послужила причиной некоторых очень изобретательных предположений. но остается неопределенным. В любом случае для объединения суперструн критический размер, в котором зависимость φ уничтожается предпочтительнее, так как в большинстве предложений о том, как выйти наружу критического измерения, можно ожидать потери безмассового частицы, находящиеся в критическом измерении.
Примечание: это не исключает использования некритической теории струн. в физике адронов, где все связанные состояния массивны. Здесь только самосогласованность теории, особенно ее Лоренц-инвариантность необходима.