Графики Клейна

В математической области теории графов графы Клейна представляют собой два разных, но связанных между собой регулярных графа , каждый из которых имеет 84 ребра. Каждый из них может быть вложен в ориентируемую поверхность рода 3 , в которой они образуют двойственные графы .
Кубический граф Клейна
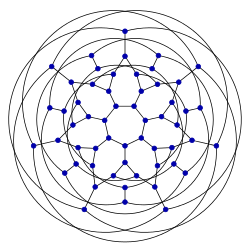
[ редактировать ]| 3-регулярный граф Клейна | |
|---|---|
 | |
| Назван в честь | Феликс Кляйн |
| Вершины | 56 |
| Края | 84 |
| Радиус | 6 |
| Диаметр | 6 |
| Обхват | 7 |
| Автоморфизмы | 336 |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Симметричный Кубический гамильтониан |
| Таблица графиков и параметров | |
Это 3- правильный ( кубический ) граф с 56 вершинами и 84 ребрами, названный в честь Феликса Кляйна .
Он гамильтонов , имеет хроматическое число 3, хроматический индекс 3, радиус 6, диаметр 6 и обхват 7. Это также 3- вершинно-связный и 3- реберно-связный граф. Имеет толщину книги 3 и номер очереди 2. [1]
Его можно встроить в рода ориентируемую поверхность -3 (которую можно представить как квартику Клейна ), где он образует отображение Клейна с 24 семиугольными гранями, символ Шлефли {7,3} 8 .
Согласно переписи Фостера , граф Клейна, обозначаемый как F056B, является единственным кубически-симметричным графом с 56 вершинами, который не является двудольным . [2]
Его можно получить из 28-вершинного графа Коксетера . [3]
Алгебраические свойства
[ редактировать ]Группой автоморфизмов графа Клейна является группа PGL 2 (7) порядка 336, имеющая PSL 2 (7) как нормальная подгруппа. Эта группа действует транзитивно на своих полуребрах, поэтому граф Клейна является симметричным графом .
Характеристический многочлен этого 56-вершинного графа Клейна равен
 |  |
7-регулярный граф Клейна
[ редактировать ]| 7-регулярный граф Клейна | |
|---|---|
 | |
| Назван в честь | Феликс Кляйн |
| Вершины | 24 |
| Края | 84 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 3 |
| Автоморфизмы | 336 |
| Хроматическое число | 4 |
| Хроматический индекс | 7 |
| Характеристики | Симметричный гамильтониан |
| Таблица графиков и параметров | |
Это 7- правильный граф с 24 вершинами и 84 ребрами, названный в честь Феликса Кляйна .
Он гамильтонов , имеет хроматическое число 4, хроматический индекс 7, радиус 3, диаметр 3 и обхват 3.
Его можно встроить в ориентируемую поверхность рода 3, где он образует двойственное отображение Клейна с 56 треугольными гранями, символом Шлефли {3,7} 8 . [4]
Это уникальный дистанционно регулярный граф с массивом пересечений. ; однако это не дистанционно-транзитивный граф . [5]
Алгебраические свойства
[ редактировать ]Группа автоморфизмов 7-валентного графа Клейна — это та же группа порядка 336, что и кубического отображения Клейна, также действующая транзитивно на его полуребрах.
Характеристический многочлен этого 24-вершинного графа Клейна равен . [6]

Ссылки
[ редактировать ]- ^ Вольц, Джессика; Проектирование линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.
- ^ Кондер, М .; Добчани, П. (2002). «Трёхвалентные симметричные графы до 768 вершин». Дж. Комбин. Математика. Комбинировать. Вычислить . 40 : 41–63. .
- ^ Дейтер, Итало Дж. (2012). «От графа Кокстера к графу Клейна». Журнал теории графов . 70 (1): 1–9. arXiv : 1002.1960 . дои : 10.1002/jgt.20597 . МР 2916063 .
- ^ Шульте, Эгон; Уиллс, Дж. М. (1985). «Многогранная реализация отображения Феликса Клейна {3, 7} 8 на римановой поверхности рода 3» . Дж. Лондон Математика. Соц . с2-32(3): 539–547. дои : 10.1112/jlms/s2-32.3.539 .
- ^ Брауэр, Андриес ; Коэн, Арье; Ноймайер, Арнольд (1989). Дистанционно-регулярные графы . Издательство Спрингер . п. 386 . ISBN 978-0-387-50619-7 .
- ^ ван Дам, скорая помощь; Хемерс, штат Вашингтон; Кулен, Дж. Х.; Спенс, Э. (2006). «Характеризация дистанционной регулярности графов по спектру» . Дж. Комбин. Теория Сер. А. 113 (8): 1805–1820. дои : 10.1016/j.jcta.2006.03.008 .


