15 пазлов

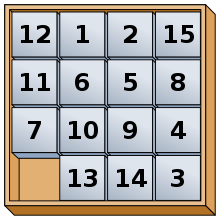
Головоломка «15» (также называемая «Головоломка с драгоценными камнями» , «Головоломка с боссом» , «Игра пятнадцати» , «Мистический квадрат» и другими) представляет собой скользящую головоломку . Он состоит из 15 квадратных плиток с номерами от 1 до 15 в рамке, имеющей 4 позиции плитки в высоту и 4 позиции плитки в ширину, с одной незанятой позицией. Плитки в том же ряду или столбце открытого положения можно перемещать, сдвигая их по горизонтали или по вертикали соответственно. Цель головоломки — разместить плитки в числовом порядке (слева направо, сверху вниз).

Головоломка из 15, названная в честь количества плиток в рамке, также может называться «головоломкой из 16» , имея в виду ее общую вместимость плиток. Похожие названия используются для вариантов головоломки 15 разного размера, например головоломки 8, в которой 8 плиток в рамке 3×3.

Головоломка n — это классическая задача моделирования алгоритмов, включающих эвристику . Обычно используемые эвристики для решения этой задачи включают подсчет количества неуместных плиток и нахождение суммы расстояний на такси между каждым блоком и его положением в конфигурации цели. ^[1] Обратите внимание, что оба варианта допустимы . То есть они никогда не переоценивают количество оставшихся ходов, что обеспечивает оптимальность для определенных алгоритмов поиска, таких как A* . ^[1]

Математика

Разрешимость

Джонсон и Стори (1879) использовали аргумент четности , чтобы показать, что половину исходных позиций головоломки n невозможно решить, независимо от того, сколько ходов будет сделано. Это делается путем рассмотрения бинарной функции конфигурации плитки, которая инвариантна при любом допустимом перемещении, а затем использования ее для разделения пространства всех возможных помеченных состояний на два взаимно недоступных класса эквивалентности одинакового размера. Это означает, что половина всех позиций неразрешимы, хотя об оставшейся половине здесь ничего не говорится.

Инвариант — это четность перестановки всех 16 квадратов плюс четность расстояния такси (количество строк плюс количество столбцов) до пустого квадрата от правого нижнего угла. Это инвариант, поскольку каждый ход меняет как четность перестановки, так и четность расстояния до такси. В частности, если пустой квадрат находится в правом нижнем углу, то головоломка разрешима только в том случае, если перестановка остальных частей четная.

Джонсон и Стори (1879) также показали, что на досках размера m × n , где m и n больше или равны 2, все четные перестановки разрешимы . Это можно доказать индукцией по m и n , начиная с m = n = 2. Это означает, что существует ровно два класса эквивалентности взаимодоступных механизмов и что описанная четность является единственным нетривиальным инвариантом, хотя существуют эквивалентные описания. .

Арчер (1999) дал другое доказательство, основанное на определении классов эквивалентности через гамильтонов путь .

Уилсон (1974) изучал обобщение головоломки 15 на произвольные конечные графы , исходной проблемой был случай сеточного графа 4×4 . У задачи есть некоторые вырожденные случаи, когда ответ либо тривиален, либо представляет собой простую комбинацию ответов на одну и ту же задачу в некоторых подграфах. А именно, для путей и многоугольников головоломка не имеет свободы; если граф несвязен , важна только компонента связности вершины с «пустым местом»; а если существует вершина сочленения , то задача сводится к одной и той же головоломке на каждом из двусвязных компонентов этой вершины. Исключив эти случаи, Уилсон показал, что, кроме одного исключительного графа с 7 вершинами, можно получить все перестановки, если только граф не является двудольным , и в этом случае могут быть получены именно четные перестановки. Исключительный граф представляет собой правильный шестиугольник с одной диагональю и добавленной вершиной в центре; только ⁠ 1/6 его перестановок ⁠ может быть достигнуто, что дает пример экзотического вложения S ₅ в S ₆ .

Для более крупных версий головоломки n найти решение несложно. Однако задача поиска кратчайшего решения NP-трудна . Также NP-трудно аппроксимировать наименьшее количество слайдов в пределах аддитивной константы, но существует аппроксимация с полиномиальным коэффициентом постоянной времени. ^[2]^[3] Для головоломки из 15 длина оптимальных решений варьируется от 0 до 80 ходов по одной плитке (есть 17 конфигураций, требующих 80 ходов). ^[4]^[5] или 43 хода с несколькими плитками; ^[6] Головоломку 8 всегда можно решить не более чем за 31 ход по одной плитке или за 24 хода по нескольким плиткам (целочисленная последовательность A087725 ). Метрика нескольких плиток подсчитывает последующие перемещения пустой плитки в том же направлении, что и первая. ^[6]

Число возможных позиций головоломки из 24 ⁠ 25! / 2 ⁠ ≈ 7.76 × 10 ²⁴, что слишком много, чтобы реально вычислить число Бога , используя методы грубой силы. В 2011 году были установлены нижние границы для 152 ходов с одной плиткой или 41 хода с несколькими плитками, а также верхние границы для 208 ходов с одной плиткой или 109 ходов с несколькими плитками. ^[7]^[8]^[9]^[10] В 2016 году верхняя граница была улучшена до 205 ходов по одной плитке. ^[11]

Теория групп

Преобразования головоломки 15 образуют группоид (а не группу, поскольку не все ходы могут быть составлены); ^[12]^[13]^[14] этот группоид действует на конфигурации.

Поскольку комбинации головоломки 15 могут быть созданы с помощью 3-циклов , можно доказать, что головоломка 15 может быть представлена чередующейся группой. $A_{15}$ . ^[15] Фактически, любой $2k-1$ раздвижную головоломку с квадратными плитками одинакового размера можно представить в виде $A_{2k-1}$ .

История

Сэма Лойда Неразрешимая головоломка «15», в которой поменяны местами плитки 14 и 15. Эта головоломка неразрешима, поскольку для перевода ее в решенное состояние потребуется изменение инварианта.

Загадку «придумал» Нойес Палмер Чепмен. ^[16] почтмейстер из Канастоты, штат Нью-Йорк , который, как говорят, еще в 1874 году показал друзьям головоломку-предшественницу, состоящую из 16 пронумерованных блоков, которые нужно было собрать в ряды по четыре, каждый из которых в сумме давал бы 34 (см. магический квадрат ). Копии улучшенной головоломки 15 попали в Сиракузы, штат Нью-Йорк , через сына Чепмена, Фрэнка, а оттуда, через различные связи, в Уотч-Хилл, Род-Айленд , и, наконец, в Хартфорд , Коннектикут , где студенты в Америке Школа для глухих приступила к изготовлению пазла. К декабрю 1879 года они были проданы как на местном уровне, так и в Бостоне , штат Массачусетс . Показанный на одном из них Маттиас Райс, который управлял деревообрабатывающим бизнесом в Бостоне, начал производство головоломок где-то в декабре 1879 года и убедил торговца модными товарами «Янки Нотионс» продавать их под названием «Гем-головоломка». В конце января 1880 года Чарльз Пиви, дантист из Вустера , штат Массачусетс, привлек к себе внимание, предложив денежное вознаграждение за решение головоломки 15. ^[16]

Игра стала повальным увлечением в США в 1880 году. ^[17]

Чепмен подал заявку на патент на свою «головоломку-пасьянс» 21 февраля 1880 года. Однако этот патент был отклонен, вероятно, потому, что он недостаточно отличался от патента на «головоломки-блоки» от 20 августа 1878 года (US 207124), выданного Эрнест У. Кинси. ^[16]

Сэм Ллойд

С 1891 года и до своей смерти в 1911 году Сэм Лойд утверждал, что изобрел головоломку. Однако Лойд не имел никакого отношения к изобретению или первоначальной популярности головоломки. Первая статья Лойда о головоломке была опубликована в 1886 году, и только в 1891 году он впервые заявил, что является изобретателем. ^[16]^[18]

Некоторый более поздний интерес был вызван предложением Лойда о призе в размере 1000 долларов (что эквивалентно 33 911 долларам в 2023 году) любому, кто сможет предложить решение для достижения определенной комбинации, указанной Лойдом, а именно перестановки 14 и 15, которую Лойд назвал головоломкой 14-15. . ^[1] Это невозможно, как было показано более десяти лет назад Джонсоном и Стори (1879) , потому что это требует преобразования от четной перестановки к нечетной.

Разновидности головоломки 15

« Минус-куб» , выпускаемый в СССР , представляет собой 3D- головоломку с операциями, аналогичными «Пазлу 15».

Версии головоломки из 15 включают в себя разное количество плиток, например, головоломку из 8 или 24 головоломки.

Поп-культура

Чемпион мира по шахматам Бобби Фишер был экспертом в решении головоломки «15». ^[19] Он был рассчитан на то, чтобы решить ее за 25 секунд; Фишер продемонстрировал это 8 ноября 1972 года в программе «Вечернее шоу» с Джонни Карсоном . ^[20]^[21]

См. также

Комбинированные головоломки
Jeu de taquin , операция по перекосу картин Янга, похожая на ходы головоломки «15».
Клоцкий
Механические головоломки
Проблемы с движением гальки
Кубик Рубика
Задача о трех чашках

Примечания

^ Перейти обратно: ^а ^б ^с Корф, RE (2000), «Последние достижения в разработке и анализе допустимых эвристических функций» (PDF) , в Choueiry, BY; Уолш Т. (ред.), Абстракция, переформулировка и аппроксимация (PDF) , SARA 2000. Конспекты лекций по информатике, том. 1864, Шпрингер, Берлин, Гейдельберг, стр. 45–55, номер документа : 10.1007/3-540-44914-0_3 , ISBN. 978-3-540-67839-7 , заархивировано из оригинала (PDF) 16 августа 2010 г. , получено 26 апреля 2010 г.
^ Ратнер, Дэниел; Вармут, Манфред (1986). «Найти кратчайшее решение для расширения N × N загадки из 15 сложно» (PDF) . Национальная конференция по искусственному интеллекту . Архивировано (PDF) из оригинала 9 марта 2012 г.
^ Ратнер, Дэниел; Вармут, Манфред (1990). "Затем ²−1)-головоломка и связанные с ней проблемы перемещения» . Журнал символических вычислений . 10 (2): 111–137. doi : 10.1016/S0747-7171(08)80001-6 .
^ Ричард Э. Корф, Неявный поиск по диску в линейном времени , Журнал ACM, том 55, выпуск 6 (декабрь 2008 г.), статья 26, стр. 29-30. «Для головоломки пятнадцати 4 × 4 существует 17 различных состояний на глубине 80 ходов от исходного состояния с пробелом в углу, а для головоломки пятнадцати 2 × 8 есть уникальное состояние с максимальным состоянием 140. выходит из исходного состояния».
^ А. Брюнгер, А. Марцетта, К. Фукуда и Дж. Нивергельт, Стенд параллельного поиска ZRAM и его приложения , Annals of Operations Research 90 (1999), стр. 45–63.
: «Гассер нашел 9 позиций, требующих 80 ходов... Теперь мы доказали, что самые сложные позиции из 15 головоломок фактически требуют 80 ходов. Мы также обнаружили две ранее неизвестные позиции, для решения которых требуется ровно 80 ходов».
^ Перейти обратно: ^а ^б «Загадку пятнадцати можно решить за 43 «хода»» . Домен форума Cube
^ «24 головоломки, новая нижняя граница: 152» . Домен форума Cube
^ «Загадка m × n (современное состояние)» . Раздвижной уголок-головоломка с плиткой.
^ «208 для 5х5» . Домен форума Cube.
^ «5x5 можно решить за 109 MTM» . Домен форума Cube.
^ «Раздвижную головоломку 5x5 можно решить за 205 ходов» . Домен форума Cube.
^ Джим Белк (2008) Головоломки, группы и группоиды , Семинар «Все»
^ Группоид из 15 головоломок (1) , Never Ending Books
^ Группоид из 15 головоломок (2) , Never Ending Books
^ Билер, Роберт. «Загадка пятнадцати: мотивирующий пример для меняющейся группы» (PDF) . факультет.etsu.edu /. Государственный университет Восточного Теннесси. Архивировано из оригинала (PDF) 7 января 2021 года . Проверено 26 декабря 2020 г.
^ Перейти обратно: ^а ^б ^с ^д Головоломка «15» , Джерри Слокам и Дик Зонневельд, 2006 г. ISBN 1-890980-15-3
^ Слокум и Сингмастер (2009 , стр. 15)
^ Барри Р. Кларк, Головоломки для удовольствия , стр. 10–12, Cambridge University Press, 1994. ISBN 0-521-46634-2 .
^ Клиффорд А. Пиковер, Книга математики: от Пифагора до 57-го измерения, 250 вех в истории математики , с. 262, Стерлинг Паблишинг, 2009 г. ISBN 1402757964 .
^ «Бобби Фишер решает головоломку из 15 за 17 секунд на вечернем шоу Карсона - 08.11.1972» , Вечернее шоу , 8 ноября 1972 года, Johnny Carson Productions, получено 1 августа 2021 года.
^ Адам Спенсер, Большая книга чисел Адама Спенсера: все, что вы хотели знать о числах от 1 до 100 , стр. 58, издательство Brio Books, 2014 г. ISBN 192113433X .

Ссылки

Арчер, Аарон Ф. (1999), «Современная трактовка головоломки 15», The American Mathematical Monthly , 106 (9): 793–799, CiteSeerX 10.1.1.19.1491 , doi : 10.2307/2589612 , ISSN 0002-9890 , JSTOR 2589612 , MR 1732661
Джонсон, Вм. Вулси; Стори, Уильям Э. (1879), «Заметки о головоломке «15», American Journal of Mathematics , 2 (4): 397–404, doi : 10.2307/2369492 , ISSN 0002-9327 , JSTOR 2369492
Эдвард Каснер и Джеймс Ньюман (1940) Математика и воображение , стр. 177–80, Саймон и Шустер .
Слокам, Джерри; Сингмастер, Дэвид (2009). Куб: полное руководство по самой продаваемой в мире головоломке — секреты, истории, решения . Черный Пес и Левенталь . ISBN 978-1579128050 .
Уилсон, Ричард М. (1974), «Загадки с графами, гомотопия и знакопеременная группа», Журнал комбинаторной теории, серия B , 16 : 86–96, doi : 10.1016/0095-8956(74)90098-7 , ISSN 0095-8956 , МР 0332555

Внешние ссылки

[Korf,2000-1] Перейти обратно: ^а ^б ^с Корф, RE (2000), «Последние достижения в разработке и анализе допустимых эвристических функций» (PDF) , в Choueiry, BY; Уолш Т. (ред.), Абстракция, переформулировка и аппроксимация (PDF) , SARA 2000. Конспекты лекций по информатике, том. 1864, Шпрингер, Берлин, Гейдельберг, стр. 45–55, номер документа : 10.1007/3-540-44914-0_3 , ISBN. 978-3-540-67839-7 , заархивировано из оригинала (PDF) 16 августа 2010 г. , получено 26 апреля 2010 г.

[Ratner1986-2] Ратнер, Дэниел; Вармут, Манфред (1986). «Найти кратчайшее решение для расширения N × N загадки из 15 сложно» (PDF) . Национальная конференция по искусственному интеллекту . Архивировано (PDF) из оригинала 9 марта 2012 г.

[ratner+warmuth-3] Ратнер, Дэниел; Вармут, Манфред (1990). "Затем ²−1)-головоломка и связанные с ней проблемы перемещения» . Журнал символических вычислений . 10 (2): 111–137. doi : 10.1016/S0747-7171(08)80001-6 .

[4] Ричард Э. Корф, Неявный поиск по диску в линейном времени , Журнал ACM, том 55, выпуск 6 (декабрь 2008 г.), статья 26, стр. 29-30. «Для головоломки пятнадцати 4 × 4 существует 17 различных состояний на глубине 80 ходов от исходного состояния с пробелом в углу, а для головоломки пятнадцати 2 × 8 есть уникальное состояние с максимальным состоянием 140. выходит из исходного состояния».

[5] А. Брюнгер, А. Марцетта, К. Фукуда и Дж. Нивергельт, Стенд параллельного поиска ZRAM и его приложения , Annals of Operations Research 90 (1999), стр. 45–63.
: «Гассер нашел 9 позиций, требующих 80 ходов... Теперь мы доказали, что самые сложные позиции из 15 головоломок фактически требуют 80 ходов. Мы также обнаружили две ранее неизвестные позиции, для решения которых требуется ровно 80 ходов».

[multi-tile-6] Перейти обратно: ^а ^б «Загадку пятнадцати можно решить за 43 «хода»» . Домен форума Cube

[7] «24 головоломки, новая нижняя граница: 152» . Домен форума Cube

[8] «Загадка m × n (современное состояние)» . Раздвижной уголок-головоломка с плиткой.

[9] «208 для 5х5» . Домен форума Cube.

[10] «5x5 можно решить за 109 MTM» . Домен форума Cube.

[11] «Раздвижную головоломку 5x5 можно решить за 205 ходов» . Домен форума Cube.

[12] Джим Белк (2008) Головоломки, группы и группоиды , Семинар «Все»

[13] Группоид из 15 головоломок (1) , Never Ending Books

[14] Группоид из 15 головоломок (2) , Never Ending Books

[15] Билер, Роберт. «Загадка пятнадцати: мотивирующий пример для меняющейся группы» (PDF) . факультет.etsu.edu /. Государственный университет Восточного Теннесси. Архивировано из оригинала (PDF) 7 января 2021 года . Проверено 26 декабря 2020 г.

[slocum-sonneveld-16] Перейти обратно: ^а ^б ^с ^д Головоломка «15» , Джерри Слокам и Дик Зонневельд, 2006 г. ISBN 1-890980-15-3

[17] Слокум и Сингмастер (2009 , стр. 15)

[18] Барри Р. Кларк, Головоломки для удовольствия , стр. 10–12, Cambridge University Press, 1994. ISBN 0-521-46634-2 .

[19] Клиффорд А. Пиковер, Книга математики: от Пифагора до 57-го измерения, 250 вех в истории математики , с. 262, Стерлинг Паблишинг, 2009 г. ISBN 1402757964 .

[20] «Бобби Фишер решает головоломку из 15 за 17 секунд на вечернем шоу Карсона - 08.11.1972» , Вечернее шоу , 8 ноября 1972 года, Johnny Carson Productions, получено 1 августа 2021 года.

[21] Адам Спенсер, Большая книга чисел Адама Спенсера: все, что вы хотели знать о числах от 1 до 100 , стр. 58, издательство Brio Books, 2014 г. ISBN 192113433X .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]