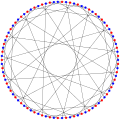
Граф Фостера
| Граф Фостера | |
|---|---|
 Граф Фостера | |
| Назван в честь | Рональд Мартин Фостер |
| Вершины | 90 |
| Края | 135 |
| Радиус | 8 |
| Диаметр | 8 |
| Обхват | 10 |
| Автоморфизмы | 4320 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Номер очереди | 2 |
| Характеристики | Кубический двусторонний Симметричный гамильтониан Дистанционно-транзитивный |
| Таблица графиков и параметров | |
В математической области теории графов граф Фостера представляет собой двудольный 3- регулярный граф с 90 вершинами и 135 ребрами. [1]
Граф Фостера является гамильтоновым и имеет хроматическое число 2, хроматический индекс 3, радиус 8, диаметр 8 и обхват 10. Это также 3 -связный граф и 3 -связный граф. У нее номер очереди 2, а верхняя граница толщины книги равна 4. [2]
Все кубически- дистанционно-регулярные графы известны. [3] Граф Фостера — один из 13 таких графов. Это уникальный дистанционно-транзитивный граф с массивом пересечений {3,2,2,2,2,1,1,1;1,1,1,1,2,2,2,3}. [4] Его можно построить как граф инцидентности частичного линейного пространства , которое представляет собой единственное тройное накрытие без восьмиугольников обобщенного четырехугольника GQ (2,2) . Он назван в честь Фостера , чья Фостеровская перепись кубических Р. М. симметричных графов включала этот граф.
Двудольная половина графа Фостера представляет собой дистанционно регулярный граф и локально линейный граф . Это один из конечного числа таких графов шестой степени. [5]
Алгебраические свойства
[ редактировать ]Группа автоморфизмов графа Фостера — это группа порядка 4320. [6] Он действует транзитивно на вершинах, ребрах и дугах графа. Следовательно, граф Фостера является симметричным графом . Он имеет автоморфизмы, которые переводят любую вершину в любую другую вершину и любое ребро в любое другое ребро. Согласно переписи Фостера , граф Фостера, обозначаемый как F90A, является единственным кубически-симметричным графом с 90 вершинами. [7]
Характеристический полином графа Фостера равен .
Галерея
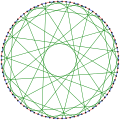
[ редактировать ]- График Фостера раскрашен для выделения различных циклов.
- Хроматическое число графа Фостера равно 2.
- Хроматический индекс графа Фостера равен 3.
Ссылки
[ редактировать ]- ^ Вайсштейн, Эрик В. «График Фостера» . Математический мир .
- ^ Вольц, Джессика; Проектирование линейных макетов с помощью SAT. Магистерская диссертация, Тюбингенский университет, 2018 г.
- ^ Брауэр, А.Э.; Коэн, AM; и Ноймайер А. Дистанционно-регулярные графы. Нью-Йорк: Springer-Verlag, 1989.
- ^ Кубические дистанционно-регулярные графы , А. Брауэр.
- ^ Хираки, Акира; Номура, Казумаса; Судзуки, Хироши (2000), «Дистанционно-регулярные графы валентности 6 и ", Журнал алгебраической комбинаторики , 11 (2): 101–134, doi : 10.1023/A:1008776031839 , MR 1761910
- ^ «Граф Фостера G-12» , Энциклопедия графиков , получено 26 февраля 2024 г.
- ^ Кондер М. и Добчани П. «Трехвалентные симметричные графы до 768 вершин». Дж. Комбин. Математика. Комбинировать. Вычислить. 40, 41–63, 2002.
- Биггс, Нидерланды; Бошир, АГ; Шоу-Тейлор, Дж. (1986), «Кубические дистанционно регулярные графы», Журнал Лондонского математического общества , 33 (3): 385–394, doi : 10.1112/jlms/s2-33.3.385 , MR 0850954 .
- Ван Дам, Эдвин Р.; Хемерс, Виллем Х. (2002), «Спектральные характеристики некоторых дистанционно регулярных графов», Журнал алгебраической комбинаторики , 15 (2): 189–202, doi : 10.1023/A:1013847004932 , MR 1887234 .
- Ван Малдегем, Хендрик (2002), «Десять исключительных геометрий из трехвалентных дистанционных регулярных графов», Annals of Combinatorics , 6 (2): 209–228, doi : 10.1007/PL00012587 , MR 1955521 , S2CID 195315348 .