доля Роша

В астрономии полость Роша — это область вокруг звезды в двойной системе, внутри которой вращающийся материал гравитационно связан с этой звездой. Это примерно каплевидная область, ограниченная критическим гравитационным эквипотенциалом , вершина которой направлена в сторону другой звезды (вершина находится в L ₁ лагранжевой точке системы ).

Полость Роша отличается от сферы Роша , которая аппроксимирует гравитационную сферу влияния одного астрономического тела перед лицом возмущений со стороны более массивного тела, вокруг которого оно вращается. Он также отличается от предела Роша , который представляет собой расстояние, на котором объект, удерживаемый вместе только силой тяжести, начинает разрушаться из-за приливных сил . Полость Роша, предел Роша и сфера Роша названы в честь французского астронома Эдуарда Роша .

Определение

Трехмерное представление потенциала Роша в двойной звезде с отношением масс 2 в системе отсчета, вращающейся вместе. Фигуры в форме капель на эквипотенциальном графике внизу рисунка определяют то, что считается лепестками Роша звезд. L ₁ , L ₂ и L ₃ — точки Лагранжа , в которых силы (рассматриваемые во вращающейся системе отсчета) уравновешиваются. Масса может перетекать через точку седла L ₁ от одной звезды к ее спутнику, если звезда заполняет свою полость Роша. ^[1]

В двойной системе с круговой орбитой часто бывает полезно описать систему в системе координат, вращающейся вместе с объектами. В этой неинерциальной системе отсчета необходимо учитывать центробежную силу помимо гравитации . Оба вместе могут быть описаны потенциалом , так что, например, поверхности звезд лежат вдоль эквипотенциальных поверхностей.

Рядом с каждой звездой поверхности с равным гравитационным потенциалом имеют примерно сферическую форму и концентричны с ближайшей звездой. Вдали от звездной системы эквипотенциалы имеют примерно эллипсоидную форму и вытянуты параллельно оси, соединяющей звездные центры. Критический эквипотенциал пересекает себя в системы L ₁ лагранжевой точке , образуя двухлепестковую восьмерку с одной из двух звезд в центре каждой доли. Этот критический эквипотенциал определяет доли Роша. ^[2]

Там, где материя движется относительно вращающейся в одном направлении системы, на нее будет действовать сила Кориолиса . Это невозможно вывести из модели доли Роша, поскольку сила Кориолиса является неконсервативной силой (т. е. не может быть представлена скалярным потенциалом ).

Дальнейший анализ

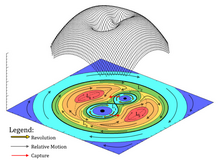
На графиках гравитационного потенциала L1 _, L2 _, L3 _, L4 _, L5 _{находятся} в синхронном вращении с системой. Области красного, оранжевого, желтого, зеленого, голубого и синего цветов представляют собой потенциальные массивы от высокого до низкого. Красные стрелки — вращение системы, черные — относительные движения обломков.

Обломки перемещаются быстрее в области с более низким потенциалом и медленнее в области с более высоким потенциалом. Таким образом, относительные движения мусора на нижней орбите направлены в одном направлении с вращением системы, а на более высокой орбите — в противоположном направлении.

L ₁ – точка равновесия гравитационного захвата. Это точка гравитационного отсечения двойной звездной системы. Это минимальное потенциальное равновесие между _L1 , _L2 , _L3 , _L4 и _L5 . Это самый простой способ перемещения обломков между сферой Хилла (внутренний круг синего и голубого цветов) и общими гравитационными областями (восьмерки желтого и зеленого цветов на внутренней стороне).

L ₂ и L ₃ — точки равновесия гравитационного возмущения. Проходя через эти две точки равновесия, обломки могут перемещаться между внешней областью (желтые и зеленые восьмерки на внешней стороне) и общей гравитационной областью двойной системы.

L ₄ и L ₅ – точки максимального потенциала в системе. Это неустойчивые равновесия. Если соотношение масс двух звезд станет больше, то оранжевая, желтая и зеленая области превратятся в подковообразную орбиту .

Красная область станет орбитой головастика .

Массовый трансфер

Когда звезда «превышает свою полость Роша», ее поверхность выходит за пределы ее полости Роша, и материал, лежащий за пределами полости Роша, может «упасть» в полость Роша другого объекта через первую точку Лагранжа. В бинарной эволюции это называется массопереносом через переполнение полости Роша .

В принципе, массоперенос может привести к полному распаду объекта, поскольку уменьшение массы объекта приводит к сокращению его доли Роша. Однако есть несколько причин, почему этого не происходит в целом. Во-первых, уменьшение массы звезды-донора может привести к уменьшению звезды-донора, что, возможно, предотвратит такой результат. Во-вторых, при переносе массы между двумя компонентами двойной системы угловой момент передается и .В то время как передача массы от более массивного донора к менее массивному аккретору обычно приводит к сокращению орбиты, обратный процесс приводит к расширению орбиты (в предположении сохранения массы и углового момента). Расширение двойной орбиты приведет к менее резкому сокращению или даже расширению доли Роша донора, часто предотвращая разрушение донора.

Чтобы определить стабильность массопереноса и, следовательно, точную судьбу звезды-донора, необходимо принять во внимание, как радиус звезды-донора и ее полости Роша реагируют на потерю массы донора; если звезда в течение длительного времени расширяется быстрее, чем ее полость Роша, или сжимается медленнее, чем ее полость Роша, массоперенос будет нестабильным, и звезда-донор может распасться. Если звезда-донор расширяется медленнее или сжимается быстрее, чем ее полость Роша, массообмен в целом будет стабильным и может продолжаться в течение длительного времени.

Перенос массы из-за переполнения полости Роша ответственен за ряд астрономических явлений, включая системы Алголя , повторяющиеся новые звезды ( двойные звезды, состоящие из красного гиганта и белого карлика , которые находятся достаточно близко, чтобы вещество красного гиганта стекало на белый карлик), рентгеновские двойные системы и миллисекундные пульсары . Такой массоперенос за счет переполнения лепестков Роша (RLOF) далее разбивается на три отдельных случая:

Случай А: Случай A RLOF возникает, когда звезда-донор горит водородом . По мнению Нельсона и Эгглтона, существует ряд подклассов. ^[3] которые воспроизведены здесь:
AD динамический: когда RLOF происходит со звездой с глубокой зоной конвекции . Перенос массы происходит быстро в динамическом масштабе времени звезды и может закончиться полным слиянием .
AR быстрый контакт: аналогично AD, но по мере того, как звезда, на которую быстро нарастает материя, набирает массу, она приобретает физический размер, достаточный для того, чтобы достичь своей собственной полости Роша. В такие моменты система проявляется как контактная двоичная переменная , такая как переменная W Ursae Majoris .
AS медленный контакт: похож на AR, но происходит только короткий период быстрого массопереноса, за которым следует гораздо более длительный период медленного массопереноса. В конце концов звезды вступят в контакт, но к тому моменту, когда это произойдет, они существенно изменились. Переменные Алгола являются результатом таких ситуаций.
AE ранний обгон: аналогично AS, но звезда, набирающая массу, обгоняет звезду, отдающую массу, и эволюционирует за пределы главной последовательности. Звезда-донор может сжаться настолько сильно, что остановит массоперенос, но в конечном итоге массоперенос начнется снова, поскольку звездная эволюция продолжается, что приводит к случаям
AL поздний обгон: случай, когда звезда, которая изначально была донором, вспыхивает сверхновой после того, как другая звезда прошла свой собственный раунд RLOF.
AB бинарный: случай, когда звезды переключаются туда и обратно, между которыми проходит RLOF как минимум три раза (технически это подкласс вышеперечисленного).
АН без обгона: случай, когда звезда, которая изначально была донором, подвергается вспышке сверхновой до того, как другая звезда достигнет фазы RLOF.
АГ гигант: Перенос массы не начинается до тех пор, пока звезда не достигнет ветви красных гигантов , но до того, как она исчерпает свое водородное ядро (после чего система описывается как Случай Б).
Случай Б: Случай B происходит, когда RLOF запускается, в то время как донором является звезда, горящая водород после ядра / горящая водородная оболочка. Этот случай можно разделить на классы Br и Bc. ^[4] в зависимости от того, происходит ли массоперенос от звезды, в которой преобладает зона излучения (Br), и, следовательно, развивается как ситуация с большинством случаев RLOF для случая A или конвективной зоны (Bc), после которой может возникнуть фаза общей оболочки (аналогично случаю C) . ^[5] Альтернативное разделение случаев - Ba, Bb и Bc, которые примерно соответствуют фазам RLOF, которые происходят во время синтеза гелия, после синтеза гелия, но до синтеза углерода или после синтеза углерода в высокоразвитой звезде. ^[6]
Случай С: Случай C происходит, когда RLOF начинается, когда донор находится на стадии горения гелиевой оболочки или после нее. Эти системы наблюдаются реже всего, но это может быть связано с предвзятостью отбора . ^[7]

Геометрия

Точная форма доли Роша зависит от соотношения масс. $q=M_{1}/M_{2}$ , и должен оцениваться численно. Однако для многих целей полезно аппроксимировать полость Роша сферой того же объема. Приблизительная формула радиуса этой сферы:

{\frac {r_{1}}{A}}=\max {[f_{1},f_{2}]}

, для

0<q<20

где $f_{1}=0.38+0.2\log {q}$ и $f_{2}=0.46224\left({\frac {q}{1+q}}\right)^{1/3}$ .Функция $f_{1}$ больше, чем $f_{2}$ для $q\gtrsim 0.5228$ . Длина A представляет собой орбитальное расстояние системы, а r ₁ представляет собой радиус сферы, объем которой приближается к полости Роша с массой M ₁ . Точность этой формулы составляет около 2%. ^[2] Другая приближенная формула была предложена Эгглтоном и выглядит следующим образом:

{\frac {r_{1}}{A}}={\frac {0.49q^{2/3}}{0.6q^{2/3}+\ln(1+q^{1/3})}}

.

Эта формула дает результаты с точностью до 1% во всем диапазоне соотношения масс. $q$ . ^[8]

Ссылки

^ Источник
^ Перейти обратно: ^а ^б Пачински, Б. (1971). «Эволюционные процессы в тесных бинарных системах». Ежегодный обзор астрономии и астрофизики . 9 : 183–208. Бибкод : 1971ARA&A...9..183P . дои : 10.1146/annurev.aa.09.090171.001151 .
^ Нельсон, Калифорния; Эгглтон, П.П. (2001). «Полный обзор двоичной эволюции случая А со сравнением с наблюдаемыми системами типа Алголя». Астрофизический журнал . 552 (2): 664–678. arXiv : astro-ph/0009258 . Бибкод : 2001ApJ...552..664N . дои : 10.1086/320560 . S2CID 119505485 .
^ Ванбеверен, Д.; Меннекенс, Н. (01 апреля 2014 г.). «Слияние массивных двойных компактных объектов: источники гравитационных волн и места производства элементов r-процесса» . Астрономия и астрофизика . 564 : А134. arXiv : 1307.0959 . Бибкод : 2014A&A...564A.134M . дои : 10.1051/0004-6361/201322198 . ISSN 0004-6361 .
^ Ванбеверен, Д.; Ренсберген, В. ван; Лур, К. де (30 ноября 2001 г.). Самые яркие бинарные файлы . Springer Science & Business Media. ISBN 9781402003769 .
^ Бхаттачарья, Д; ван ден Хеувел, EP J (1 мая 1991 г.). «Формирование и эволюция двойных и миллисекундных радиопульсаров». Отчеты по физике . 203 (1): 1–124. Бибкод : 1991PhR...203....1B . дои : 10.1016/0370-1573(91)90064-S . ISSN 0370-1573 .
^ Подсядловский, Филипп (февраль 2014 г.). «Эволюция бинарных систем» . Аккреционные процессы в астрофизике . стр. 45–88. дои : 10.1017/CBO9781139343268.003 . ISBN 9781139343268 . Проверено 12 августа 2019 г. {{cite book}}: |website= игнорируется ( помогите )
^ Эгглтон, П.П. (1 мая 1983 г.). «Приближения радиусов лепестков Роша». Астрофизический журнал . 268 : 368. Бибкод : 1983ApJ...268..368E . дои : 10.1086/160960 .

Источники

Моррис, СЛ (февраль 1994 г.). «Два математических расширения эквипотенциалов Роша». Публикации Тихоокеанского астрономического общества . 106 (696): 154–155. Бибкод : 1994PASP..106..154M . дои : 10.1086/133361 . JSTOR 40680260 . S2CID 121386366 .
Моррис, СЛ (1 августа 1999 г.). «Пределы наклонения частных затмений двойных звезд» . Астрофизический журнал . 520 (2): 797–804. Бибкод : 1999ApJ...520..797M . дои : 10.1086/307488 .

Внешние ссылки

От горячих юпитеров к суперземлям через переполнение полости Роша - Корнелльский университет

[1] Источник

[pacz71-2] Перейти обратно: ^а ^б Пачински, Б. (1971). «Эволюционные процессы в тесных бинарных системах». Ежегодный обзор астрономии и астрофизики . 9 : 183–208. Бибкод : 1971ARA&A...9..183P . дои : 10.1146/annurev.aa.09.090171.001151 .

[3] Нельсон, Калифорния; Эгглтон, П.П. (2001). «Полный обзор двоичной эволюции случая А со сравнением с наблюдаемыми системами типа Алголя». Астрофизический журнал . 552 (2): 664–678. arXiv : astro-ph/0009258 . Бибкод : 2001ApJ...552..664N . дои : 10.1086/320560 . S2CID 119505485 .

[4] Ванбеверен, Д.; Меннекенс, Н. (01 апреля 2014 г.). «Слияние массивных двойных компактных объектов: источники гравитационных волн и места производства элементов r-процесса» . Астрономия и астрофизика . 564 : А134. arXiv : 1307.0959 . Бибкод : 2014A&A...564A.134M . дои : 10.1051/0004-6361/201322198 . ISSN 0004-6361 .

[5] Ванбеверен, Д.; Ренсберген, В. ван; Лур, К. де (30 ноября 2001 г.). Самые яркие бинарные файлы . Springer Science & Business Media. ISBN 9781402003769 .

[6] Бхаттачарья, Д; ван ден Хеувел, EP J (1 мая 1991 г.). «Формирование и эволюция двойных и миллисекундных радиопульсаров». Отчеты по физике . 203 (1): 1–124. Бибкод : 1991PhR...203....1B . дои : 10.1016/0370-1573(91)90064-S . ISSN 0370-1573 .

[7] Подсядловский, Филипп (февраль 2014 г.). «Эволюция бинарных систем» . Аккреционные процессы в астрофизике . стр. 45–88. дои : 10.1017/CBO9781139343268.003 . ISBN 9781139343268 . Проверено 12 августа 2019 г. {{cite book}}: |website= игнорируется ( помогите )

[eggleton-8] Эгглтон, П.П. (1 мая 1983 г.). «Приближения радиусов лепестков Роша». Астрофизический журнал . 268 : 368. Бибкод : 1983ApJ...268..368E . дои : 10.1086/160960 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]