Mathematical gradient operator in certain coordinate systems
This is a list of some vector calculus formulae for working with common curvilinear coordinate systems .
This article uses the standard notation ISO 80000-2 , which supersedes ISO 31-11 , for spherical coordinates (other sources may reverse the definitions of θ and φ ):The polar angle is denoted by θ ∈ [ 0 , π ] {\displaystyle \theta \in [0,\pi ]} z -axis and the radial vector connecting the origin to the point in question. The azimuthal angle is denoted by φ ∈ [ 0 , 2 π ] {\displaystyle \varphi \in [0,2\pi ]} x -axis and the projection of the radial vector onto the xy -plane. The function atan2 (y , x )arctan (y /x )domain and image . The classical arctan function has an image of (−π/2, +π/2) , whereas atan2 is defined to have an image of (−π, π] . Coordinate conversions [ edit ] Conversion between Cartesian, cylindrical, and spherical coordinates[1] From Cartesian Cylindrical Spherical To Cartesian x = x y = y z = z {\displaystyle {\begin{aligned}x&=x\\y&=y\\z&=z\\\end{aligned}}} x = ρ cos φ y = ρ sin φ z = z {\displaystyle {\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}} x = r sin θ cos φ y = r sin θ sin φ z = r cos θ {\displaystyle {\begin{aligned}x&=r\sin \theta \cos \varphi \\y&=r\sin \theta \sin \varphi \\z&=r\cos \theta \\\end{aligned}}} Cylindrical ρ = x 2 + y 2 φ = arctan ( y x ) z = z {\displaystyle {\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &=\arctan \left({\frac {y}{x}}\right)\\z&=z\end{aligned}}} ρ = ρ φ = φ z = z {\displaystyle {\begin{aligned}\rho &=\rho \\\varphi &=\varphi \\z&=z\\\end{aligned}}} ρ = r sin θ φ = φ z = r cos θ {\displaystyle {\begin{aligned}\rho &=r\sin \theta \\\varphi &=\varphi \\z&=r\cos \theta \end{aligned}}} Spherical r = x 2 + y 2 + z 2 θ = arctan ( x 2 + y 2 z ) φ = arctan ( y x ) {\displaystyle {\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)\\\varphi &=\arctan \left({\frac {y}{x}}\right)\end{aligned}}} r = ρ 2 + z 2 θ = arctan ( ρ z ) φ = φ {\displaystyle {\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}}\\\theta &=\arctan {\left({\frac {\rho }{z}}\right)}\\\varphi &=\varphi \end{aligned}}} r = r θ = θ φ = φ {\displaystyle {\begin{aligned}r&=r\\\theta &=\theta \\\varphi &=\varphi \end{aligned}}}
Note that the operation arctan ( A B ) {\displaystyle \arctan \left({\frac {A}{B}}\right)} atan2 .
Unit vector conversions [ edit ] Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of destination coordinates[1] Cartesian Cylindrical Spherical Cartesian x ^ = x ^ y ^ = y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} x ^ = cos φ ρ ^ − sin φ φ ^ y ^ = sin φ ρ ^ + cos φ φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\cos \varphi {\hat {\boldsymbol {\rho }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \varphi {\hat {\boldsymbol {\rho }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} x ^ = sin θ cos φ r ^ + cos θ cos φ θ ^ − sin φ φ ^ y ^ = sin θ sin φ r ^ + cos θ sin φ θ ^ + cos φ φ ^ z ^ = cos θ r ^ − sin θ θ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\sin \theta \cos \varphi {\hat {\mathbf {r} }}+\cos \theta \cos \varphi {\hat {\boldsymbol {\theta }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \theta \sin \varphi {\hat {\mathbf {r} }}+\cos \theta \sin \varphi {\hat {\boldsymbol {\theta }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}} Cylindrical ρ ^ = x x ^ + y y ^ x 2 + y 2 φ ^ = − y x ^ + x y ^ x 2 + y 2 z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} ρ ^ = ρ ^ φ ^ = φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} ρ ^ = sin θ r ^ + cos θ θ ^ φ ^ = φ ^ z ^ = cos θ r ^ − sin θ θ ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\sin \theta {\hat {\mathbf {r} }}+\cos \theta {\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}} Spherical r ^ = x x ^ + y y ^ + z z ^ x 2 + y 2 + z 2 θ ^ = ( x x ^ + y y ^ ) z − ( x 2 + y 2 ) z ^ x 2 + y 2 + z 2 x 2 + y 2 φ ^ = − y x ^ + x y ^ x 2 + y 2 {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}+z{\hat {\mathbf {z} }}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {\left(x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}\right)z-\left(x^{2}+y^{2}\right){\hat {\mathbf {z} }}}{{\sqrt {x^{2}+y^{2}+z^{2}}}{\sqrt {x^{2}+y^{2}}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\end{aligned}}} r ^ = ρ ρ ^ + z z ^ ρ 2 + z 2 θ ^ = z ρ ^ − ρ z ^ ρ 2 + z 2 φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {\rho {\hat {\boldsymbol {\rho }}}+z{\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {z{\hat {\boldsymbol {\rho }}}-\rho {\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}} r ^ = r ^ θ ^ = θ ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}
Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of source coordinates Cartesian Cylindrical Spherical Cartesian x ^ = x ^ y ^ = y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} x ^ = x ρ ^ − y φ ^ x 2 + y 2 y ^ = y ρ ^ + x φ ^ x 2 + y 2 z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x{\hat {\boldsymbol {\rho }}}-y{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {y} }}&={\frac {y{\hat {\boldsymbol {\rho }}}+x{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} x ^ = x ( x 2 + y 2 r ^ + z θ ^ ) − y x 2 + y 2 + z 2 φ ^ x 2 + y 2 x 2 + y 2 + z 2 y ^ = y ( x 2 + y 2 r ^ + z θ ^ ) + x x 2 + y 2 + z 2 φ ^ x 2 + y 2 x 2 + y 2 + z 2 z ^ = z r ^ − x 2 + y 2 θ ^ x 2 + y 2 + z 2 {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)-y{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {y} }}&={\frac {y\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)+x{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-{\sqrt {x^{2}+y^{2}}}{\hat {\boldsymbol {\theta }}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{aligned}}} Cylindrical ρ ^ = cos φ x ^ + sin φ y ^ φ ^ = − sin φ x ^ + cos φ y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} ρ ^ = ρ ^ φ ^ = φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} ρ ^ = ρ r ^ + z θ ^ ρ 2 + z 2 φ ^ = φ ^ z ^ = z r ^ − ρ θ ^ ρ 2 + z 2 {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {\rho {\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-\rho {\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\end{aligned}}} Spherical r ^ = sin θ ( cos φ x ^ + sin φ y ^ ) + cos θ z ^ θ ^ = cos θ ( cos φ x ^ + sin φ y ^ ) − sin θ z ^ φ ^ = − sin φ x ^ + cos φ y ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\end{aligned}}} r ^ = sin θ ρ ^ + cos θ z ^ θ ^ = cos θ ρ ^ − sin θ z ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta {\hat {\boldsymbol {\rho }}}+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta {\hat {\boldsymbol {\rho }}}-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}} r ^ = r ^ θ ^ = θ ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}
Table with the del operator in cartesian, cylindrical and spherical coordinates Operation Cartesian coordinates (x , y , z ) Cylindrical coordinates (ρ , φ , z ) Spherical coordinates (r , θ , φ ) ,θ φ α Vector field A A x x ^ + A y y ^ + A z z ^ {\displaystyle A_{x}{\hat {\mathbf {x} }}+A_{y}{\hat {\mathbf {y} }}+A_{z}{\hat {\mathbf {z} }}} A ρ ρ ^ + A φ φ ^ + A z z ^ {\displaystyle A_{\rho }{\hat {\boldsymbol {\rho }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}+A_{z}{\hat {\mathbf {z} }}} A r r ^ + A θ θ ^ + A φ φ ^ {\displaystyle A_{r}{\hat {\mathbf {r} }}+A_{\theta }{\hat {\boldsymbol {\theta }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}} Gradient ∇f [1] ∂ f ∂ x x ^ + ∂ f ∂ y y ^ + ∂ f ∂ z z ^ {\displaystyle {\partial f \over \partial x}{\hat {\mathbf {x} }}+{\partial f \over \partial y}{\hat {\mathbf {y} }}+{\partial f \over \partial z}{\hat {\mathbf {z} }}} ∂ f ∂ ρ ρ ^ + 1 ρ ∂ f ∂ φ φ ^ + ∂ f ∂ z z ^ {\displaystyle {\partial f \over \partial \rho }{\hat {\boldsymbol {\rho }}}+{1 \over \rho }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}+{\partial f \over \partial z}{\hat {\mathbf {z} }}} ∂ f ∂ r r ^ + 1 r ∂ f ∂ θ θ ^ + 1 r sin θ ∂ f ∂ φ φ ^ {\displaystyle {\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}} Divergence ∇ ⋅ A [1] ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z {\displaystyle {\partial A_{x} \over \partial x}+{\partial A_{y} \over \partial y}+{\partial A_{z} \over \partial z}} 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A φ ∂ φ + ∂ A z ∂ z {\displaystyle {1 \over \rho }{\partial \left(\rho A_{\rho }\right) \over \partial \rho }+{1 \over \rho }{\partial A_{\varphi } \over \partial \varphi }+{\partial A_{z} \over \partial z}} 1 r 2 ∂ ( r 2 A r ) ∂ r + 1 r sin θ ∂ ∂ θ ( A θ sin θ ) + 1 r sin θ ∂ A φ ∂ φ {\displaystyle {1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\varphi } \over \partial \varphi }} Curl ∇ × A [1] ( ∂ A z ∂ y − ∂ A y ∂ z ) x ^ + ( ∂ A x ∂ z − ∂ A z ∂ x ) y ^ + ( ∂ A y ∂ x − ∂ A x ∂ y ) z ^ {\displaystyle {\begin{aligned}\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)&{\hat {\mathbf {z} }}\end{aligned}}} ( 1 ρ ∂ A z ∂ φ − ∂ A φ ∂ z ) ρ ^ + ( ∂ A ρ ∂ z − ∂ A z ∂ ρ ) φ ^ + 1 ρ ( ∂ ( ρ A φ ) ∂ ρ − ∂ A ρ ∂ φ ) z ^ {\displaystyle {\begin{aligned}\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right)&{\hat {\boldsymbol {\rho }}}\\+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+{\frac {1}{\rho }}\left({\frac {\partial \left(\rho A_{\varphi }\right)}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right)&{\hat {\mathbf {z} }}\end{aligned}}} 1 r sin θ ( ∂ ∂ θ ( A φ sin θ ) − ∂ A θ ∂ φ ) r ^ + 1 r ( 1 sin θ ∂ A r ∂ φ − ∂ ∂ r ( r A φ ) ) θ ^ + 1 r ( ∂ ∂ r ( r A θ ) − ∂ A r ∂ θ ) φ ^ {\displaystyle {\begin{aligned}{\frac {1}{r\sin \theta }}\left({\frac {\partial }{\partial \theta }}\left(A_{\varphi }\sin \theta \right)-{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\{}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial }{\partial r}}\left(rA_{\varphi }\right)\right)&{\hat {\boldsymbol {\theta }}}\\{}+{\frac {1}{r}}\left({\frac {\partial }{\partial r}}\left(rA_{\theta }\right)-{\frac {\partial A_{r}}{\partial \theta }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}} Laplace operator ∇2 f ≡ ∆f [1] ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + ∂ 2 f ∂ z 2 {\displaystyle {\partial ^{2}f \over \partial x^{2}}+{\partial ^{2}f \over \partial y^{2}}+{\partial ^{2}f \over \partial z^{2}}} 1 ρ ∂ ∂ ρ ( ρ ∂ f ∂ ρ ) + 1 ρ 2 ∂ 2 f ∂ φ 2 + ∂ 2 f ∂ z 2 {\displaystyle {1 \over \rho }{\partial \over \partial \rho }\left(\rho {\partial f \over \partial \rho }\right)+{1 \over \rho ^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}+{\partial ^{2}f \over \partial z^{2}}} 1 r 2 ∂ ∂ r ( r 2 ∂ f ∂ r ) + 1 r 2 sin θ ∂ ∂ θ ( sin θ ∂ f ∂ θ ) + 1 r 2 sin 2 θ ∂ 2 f ∂ φ 2 {\displaystyle {1 \over r^{2}}{\partial \over \partial r}\!\left(r^{2}{\partial f \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial \over \partial \theta }\!\left(\sin \theta {\partial f \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}} Vector gradient ∇A β ∂ A x ∂ x x ^ ⊗ x ^ + ∂ A x ∂ y x ^ ⊗ y ^ + ∂ A x ∂ z x ^ ⊗ z ^ + ∂ A y ∂ x y ^ ⊗ x ^ + ∂ A y ∂ y y ^ ⊗ y ^ + ∂ A y ∂ z y ^ ⊗ z ^ + ∂ A z ∂ x z ^ ⊗ x ^ + ∂ A z ∂ y z ^ ⊗ y ^ + ∂ A z ∂ z z ^ ⊗ z ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{x}}{\partial x}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{x}}{\partial y}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{x}}{\partial z}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{y}}{\partial x}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{y}}{\partial y}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{y}}{\partial z}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial x}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{z}}{\partial y}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}} ∂ A ρ ∂ ρ ρ ^ ⊗ ρ ^ + ( 1 ρ ∂ A ρ ∂ φ − A φ ρ ) ρ ^ ⊗ φ ^ + ∂ A ρ ∂ z ρ ^ ⊗ z ^ + ∂ A φ ∂ ρ φ ^ ⊗ ρ ^ + ( 1 ρ ∂ A φ ∂ φ + A ρ ρ ) φ ^ ⊗ φ ^ + ∂ A φ ∂ z φ ^ ⊗ z ^ + ∂ A z ∂ ρ z ^ ⊗ ρ ^ + 1 ρ ∂ A z ∂ φ z ^ ⊗ φ ^ + ∂ A z ∂ z z ^ ⊗ z ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{\rho }}{\partial \rho }}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \varphi }}-{\frac {A_{\varphi }}{\rho }}\right){\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\rho }}{\partial z}}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{\varphi }}{\partial \rho }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {A_{\rho }}{\rho }}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\varphi }}{\partial z}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial \rho }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\rho }}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}} ∂ A r ∂ r r ^ ⊗ r ^ + ( 1 r ∂ A r ∂ θ − A θ r ) r ^ ⊗ θ ^ + ( 1 r sin θ ∂ A r ∂ φ − A φ r ) r ^ ⊗ φ ^ + ∂ A θ ∂ r θ ^ ⊗ r ^ + ( 1 r ∂ A θ ∂ θ + A r r ) θ ^ ⊗ θ ^ + ( 1 r sin θ ∂ A θ ∂ φ − cot θ A φ r ) θ ^ ⊗ φ ^ + ∂ A φ ∂ r φ ^ ⊗ r ^ + 1 r ∂ A φ ∂ θ φ ^ ⊗ θ ^ + ( 1 r sin θ ∂ A φ ∂ φ + cot θ A θ r + A r r ) φ ^ ⊗ φ ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{r}}{\partial r}}{\hat {\mathbf {r} }}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {A_{\theta }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {A_{\varphi }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\theta }}{\partial r}}{\hat {\boldsymbol {\theta }}}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{\theta }}{\partial \theta }}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}-\cot \theta {\frac {A_{\varphi }}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\varphi }}{\partial r}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial A_{\varphi }}{\partial \theta }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+\cot \theta {\frac {A_{\theta }}{r}}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}\end{aligned}}} Vector Laplacian ∇2 A ≡ ∆A [2] ∇ 2 A x x ^ + ∇ 2 A y y ^ + ∇ 2 A z z ^ {\displaystyle \nabla ^{2}A_{x}{\hat {\mathbf {x} }}+\nabla ^{2}A_{y}{\hat {\mathbf {y} }}+\nabla ^{2}A_{z}{\hat {\mathbf {z} }}} ( ∇ 2 A ρ − A ρ ρ 2 − 2 ρ 2 ∂ A φ ∂ φ ) ρ ^ + ( ∇ 2 A φ − A φ ρ 2 + 2 ρ 2 ∂ A ρ ∂ φ ) φ ^ + ∇ 2 A z z ^ {\displaystyle {\begin{aligned}{\mathopen {}}\left(\nabla ^{2}A_{\rho }-{\frac {A_{\rho }}{\rho ^{2}}}-{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\rho }}}\\+{\mathopen {}}\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{\rho ^{2}}}+{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\varphi }}}\\{}+\nabla ^{2}A_{z}&{\hat {\mathbf {z} }}\end{aligned}}}
( ∇ 2 A r − 2 A r r 2 − 2 r 2 sin θ ∂ ( A θ sin θ ) ∂ θ − 2 r 2 sin θ ∂ A φ ∂ φ ) r ^ + ( ∇ 2 A θ − A θ r 2 sin 2 θ + 2 r 2 ∂ A r ∂ θ − 2 cos θ r 2 sin 2 θ ∂ A φ ∂ φ ) θ ^ + ( ∇ 2 A φ − A φ r 2 sin 2 θ + 2 r 2 sin θ ∂ A r ∂ φ + 2 cos θ r 2 sin 2 θ ∂ A θ ∂ φ ) φ ^ {\displaystyle {\begin{aligned}\left(\nabla ^{2}A_{r}-{\frac {2A_{r}}{r^{2}}}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial \left(A_{\theta }\sin \theta \right)}{\partial \theta }}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\+\left(\nabla ^{2}A_{\theta }-{\frac {A_{\theta }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}+{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Directional derivative (A ⋅ ∇)B [3] A ⋅ ∇ B x x ^ + A ⋅ ∇ B y y ^ + A ⋅ ∇ B z z ^ {\displaystyle \mathbf {A} \cdot \nabla B_{x}{\hat {\mathbf {x} }}+\mathbf {A} \cdot \nabla B_{y}{\hat {\mathbf {y} }}+\mathbf {A} \cdot \nabla B_{z}{\hat {\mathbf {z} }}} ( A ρ ∂ B ρ ∂ ρ + A φ ρ ∂ B ρ ∂ φ + A z ∂ B ρ ∂ z − A φ B φ ρ ) ρ ^ + ( A ρ ∂ B φ ∂ ρ + A φ ρ ∂ B φ ∂ φ + A z ∂ B φ ∂ z + A φ B ρ ρ ) φ ^ + ( A ρ ∂ B z ∂ ρ + A φ ρ ∂ B z ∂ φ + A z ∂ B z ∂ z ) z ^ {\displaystyle {\begin{aligned}\left(A_{\rho }{\frac {\partial B_{\rho }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\rho }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\rho }}{\partial z}}-{\frac {A_{\varphi }B_{\varphi }}{\rho }}\right)&{\hat {\boldsymbol {\rho }}}\\+\left(A_{\rho }{\frac {\partial B_{\varphi }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\varphi }}{\partial z}}+{\frac {A_{\varphi }B_{\rho }}{\rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+\left(A_{\rho }{\frac {\partial B_{z}}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{z}}{\partial \varphi }}+A_{z}{\frac {\partial B_{z}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}} ( A r ∂ B r ∂ r + A θ r ∂ B r ∂ θ + A φ r sin θ ∂ B r ∂ φ − A θ B θ + A φ B φ r ) r ^ + ( A r ∂ B θ ∂ r + A θ r ∂ B θ ∂ θ + A φ r sin θ ∂ B θ ∂ φ + A θ B r r − A φ B φ cot θ r ) θ ^ + ( A r ∂ B φ ∂ r + A θ r ∂ B φ ∂ θ + A φ r sin θ ∂ B φ ∂ φ + A φ B r r + A φ B θ cot θ r ) φ ^ {\displaystyle {\begin{aligned}\left(A_{r}{\frac {\partial B_{r}}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{r}}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{r}}{\partial \varphi }}-{\frac {A_{\theta }B_{\theta }+A_{\varphi }B_{\varphi }}{r}}\right)&{\hat {\mathbf {r} }}\\+\left(A_{r}{\frac {\partial B_{\theta }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\theta }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\theta }}{\partial \varphi }}+{\frac {A_{\theta }B_{r}}{r}}-{\frac {A_{\varphi }B_{\varphi }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(A_{r}{\frac {\partial B_{\varphi }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\varphi }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+{\frac {A_{\varphi }B_{r}}{r}}+{\frac {A_{\varphi }B_{\theta }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Tensor divergence ∇ ⋅ T γ ( ∂ T x x ∂ x + ∂ T y x ∂ y + ∂ T z x ∂ z ) x ^ + ( ∂ T x y ∂ x + ∂ T y y ∂ y + ∂ T z y ∂ z ) y ^ + ( ∂ T x z ∂ x + ∂ T y z ∂ y + ∂ T z z ∂ z ) z ^ {\displaystyle {\begin{aligned}\left({\frac {\partial T_{xx}}{\partial x}}+{\frac {\partial T_{yx}}{\partial y}}+{\frac {\partial T_{zx}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial T_{xy}}{\partial x}}+{\frac {\partial T_{yy}}{\partial y}}+{\frac {\partial T_{zy}}{\partial z}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial T_{xz}}{\partial x}}+{\frac {\partial T_{yz}}{\partial y}}+{\frac {\partial T_{zz}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}
[ ∂ T ρ ρ ∂ ρ + 1 ρ ∂ T φ ρ ∂ φ + ∂ T z ρ ∂ z + 1 ρ ( T ρ ρ − T φ φ ) ] ρ ^ + [ ∂ T ρ φ ∂ ρ + 1 ρ ∂ T φ φ ∂ φ + ∂ T z φ ∂ z + 1 ρ ( T ρ φ + T φ ρ ) ] φ ^ + [ ∂ T ρ z ∂ ρ + 1 ρ ∂ T φ z ∂ φ + ∂ T z z ∂ z + T ρ z ρ ] z ^ {\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}
[ ∂ T r r ∂ r + 2 T r r r + 1 r ∂ T θ r ∂ θ + cot θ r T θ r + 1 r sin θ ∂ T φ r ∂ φ − 1 r ( T θ θ + T φ φ ) ] r ^ + [ ∂ T r θ ∂ r + 2 T r θ r + 1 r ∂ T θ θ ∂ θ + cot θ r T θ θ + 1 r sin θ ∂ T φ θ ∂ φ + T θ r r − cot θ r T φ φ ] θ ^ + [ ∂ T r φ ∂ r + 2 T r φ r + 1 r ∂ T θ φ ∂ θ + 1 r sin θ ∂ T φ φ ∂ φ + T φ r r + cot θ r ( T θ φ + T φ θ ) ] φ ^ {\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
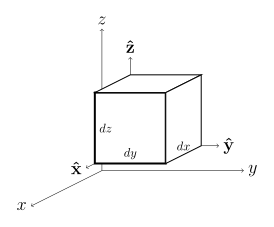
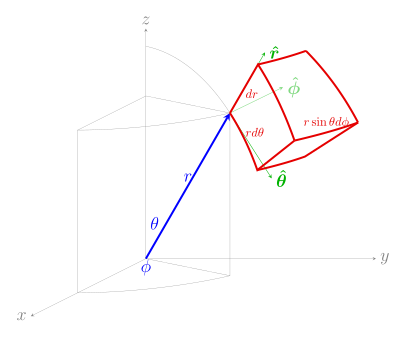
Differential displacement dℓ [1] d x x ^ + d y y ^ + d z z ^ {\displaystyle dx\,{\hat {\mathbf {x} }}+dy\,{\hat {\mathbf {y} }}+dz\,{\hat {\mathbf {z} }}} d ρ ρ ^ + ρ d φ φ ^ + d z z ^ {\displaystyle d\rho \,{\hat {\boldsymbol {\rho }}}+\rho \,d\varphi \,{\hat {\boldsymbol {\varphi }}}+dz\,{\hat {\mathbf {z} }}} d r r ^ + r d θ θ ^ + r sin θ d φ φ ^ {\displaystyle dr\,{\hat {\mathbf {r} }}+r\,d\theta \,{\hat {\boldsymbol {\theta }}}+r\,\sin \theta \,d\varphi \,{\hat {\boldsymbol {\varphi }}}} Differential normal area d S d y d z x ^ + d x d z y ^ + d x d y z ^ {\displaystyle {\begin{aligned}dy\,dz&\,{\hat {\mathbf {x} }}\\{}+dx\,dz&\,{\hat {\mathbf {y} }}\\{}+dx\,dy&\,{\hat {\mathbf {z} }}\end{aligned}}} ρ d φ d z ρ ^ + d ρ d z φ ^ + ρ d ρ d φ z ^ {\displaystyle {\begin{aligned}\rho \,d\varphi \,dz&\,{\hat {\boldsymbol {\rho }}}\\{}+d\rho \,dz&\,{\hat {\boldsymbol {\varphi }}}\\{}+\rho \,d\rho \,d\varphi &\,{\hat {\mathbf {z} }}\end{aligned}}} r 2 sin θ d θ d φ r ^ + r sin θ d r d φ θ ^ + r d r d θ φ ^ {\displaystyle {\begin{aligned}r^{2}\sin \theta \,d\theta \,d\varphi &\,{\hat {\mathbf {r} }}\\{}+r\sin \theta \,dr\,d\varphi &\,{\hat {\boldsymbol {\theta }}}\\{}+r\,dr\,d\theta &\,{\hat {\boldsymbol {\varphi }}}\end{aligned}}} Differential volume dV [1] d x d y d z {\displaystyle dx\,dy\,dz} ρ d ρ d φ d z {\displaystyle \rho \,d\rho \,d\varphi \,dz} r 2 sin θ d r d θ d φ {\displaystyle r^{2}\sin \theta \,dr\,d\theta \,d\varphi }
^α θ {\displaystyle \theta } φ {\displaystyle \varphi } θ {\displaystyle \theta } φ {\displaystyle \varphi } θ {\displaystyle \theta } φ {\displaystyle \varphi } ^β ∂ i A ⊗ e i {\displaystyle \partial _{i}\mathbf {A} \otimes \mathbf {e} _{i}} e i ⊗ ∂ i A {\displaystyle \mathbf {e} _{i}\otimes \partial _{i}\mathbf {A} } ^γ e i ⋅ ∂ i T {\displaystyle \mathbf {e} _{i}\cdot \partial _{i}\mathbf {T} } ∂ i T ⋅ e i {\displaystyle \partial _{i}\mathbf {T} \cdot \mathbf {e} _{i}} div grad f ≡ ∇ ⋅ ∇ f ≡ ∇ 2 f {\displaystyle \operatorname {div} \,\operatorname {grad} f\equiv \nabla \cdot \nabla f\equiv \nabla ^{2}f} curl grad f ≡ ∇ × ∇ f = 0 {\displaystyle \operatorname {curl} \,\operatorname {grad} f\equiv \nabla \times \nabla f=\mathbf {0} } div curl A ≡ ∇ ⋅ ( ∇ × A ) = 0 {\displaystyle \operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot (\nabla \times \mathbf {A} )=0} curl curl A ≡ ∇ × ( ∇ × A ) = ∇ ( ∇ ⋅ A ) − ∇ 2 A {\displaystyle \operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A} } Lagrange's formula for del)∇ 2 ( f g ) = f ∇ 2 g + 2 ∇ f ⋅ ∇ g + g ∇ 2 f {\displaystyle \nabla ^{2}(fg)=f\nabla ^{2}g+2\nabla f\cdot \nabla g+g\nabla ^{2}f} ∇ 2 ( P ⋅ Q ) = Q ⋅ ∇ 2 P − P ⋅ ∇ 2 Q + 2 ∇ ⋅ [ ( P ⋅ ∇ ) Q + P × ∇ × Q ] {\displaystyle \nabla ^{2}\left(\mathbf {P} \cdot \mathbf {Q} \right)=\mathbf {Q} \cdot \nabla ^{2}\mathbf {P} -\mathbf {P} \cdot \nabla ^{2}\mathbf {Q} +2\nabla \cdot \left[\left(\mathbf {P} \cdot \nabla \right)\mathbf {Q} +\mathbf {P} \times \nabla \times \mathbf {Q} \right]\quad } [4] Cartesian derivation [ edit ]
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A x ( x + d x ) d y d z − A x ( x ) d y d z + A y ( y + d y ) d x d z − A y ( y ) d x d z + A z ( z + d z ) d x d y − A z ( z ) d x d y d x d y d z = ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} =\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}&={\frac {A_{x}(x+dx)\,dy\,dz-A_{x}(x)\,dy\,dz+A_{y}(y+dy)\,dx\,dz-A_{y}(y)\,dx\,dz+A_{z}(z+dz)\,dx\,dy-A_{z}(z)\,dx\,dy}{dx\,dy\,dz}}\\&={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}
( curl A ) x = lim S ⊥ x ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( y + d y ) d z − A z ( y ) d z + A y ( z ) d y − A y ( z + d z ) d y d y d z = ∂ A z ∂ y − ∂ A y ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{x}=\lim _{S^{\perp \mathbf {\hat {x}} }\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{z}(y+dy)\,dz-A_{z}(y)\,dz+A_{y}(z)\,dy-A_{y}(z+dz)\,dy}{dy\,dz}}\\&={\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\end{aligned}}}
The expressions for ( curl A ) y {\displaystyle (\operatorname {curl} \mathbf {A} )_{y}} ( curl A ) z {\displaystyle (\operatorname {curl} \mathbf {A} )_{z}}
Cylindrical derivation [ edit ]
div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A ρ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ d z − A ρ ( ρ ) ρ d ϕ d z + A ϕ ( ϕ + d ϕ ) d ρ d z − A ϕ ( ϕ ) d ρ d z + A z ( z + d z ) d ρ ( ρ + d ρ / 2 ) d ϕ − A z ( z ) d ρ ( ρ + d ρ / 2 ) d ϕ ρ d ϕ d ρ d z = 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A ϕ ∂ ϕ + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{\rho }(\rho +d\rho )(\rho +d\rho )\,d\phi \,dz-A_{\rho }(\rho )\rho \,d\phi \,dz+A_{\phi }(\phi +d\phi )\,d\rho \,dz-A_{\phi }(\phi )\,d\rho \,dz+A_{z}(z+dz)\,d\rho \,(\rho +d\rho /2)\,d\phi -A_{z}(z)\,d\rho (\rho +d\rho /2)\,d\phi }{\rho \,d\phi \,d\rho \,dz}}\\&={\frac {1}{\rho }}{\frac {\partial (\rho A_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial A_{\phi }}{\partial \phi }}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}
( curl A ) ρ = lim S ⊥ ρ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( z ) ( ρ + d ρ ) d ϕ − A ϕ ( z + d z ) ( ρ + d ρ ) d ϕ + A z ( ϕ + d ϕ ) d z − A z ( ϕ ) d z ( ρ + d ρ ) d ϕ d z = − ∂ A ϕ ∂ z + 1 ρ ∂ A z ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\hat {\boldsymbol {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\[1ex]&={\frac {A_{\phi }(z)\left(\rho +d\rho \right)\,d\phi -A_{\phi }(z+dz)\left(\rho +d\rho \right)\,d\phi +A_{z}(\phi +d\phi )\,dz-A_{z}(\phi )\,dz}{\left(\rho +d\rho \right)\,d\phi \,dz}}\\[1ex]&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}
( curl A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( ρ ) d z − A z ( ρ + d ρ ) d z + A ρ ( z + d z ) d ρ − A ρ ( z ) d ρ d ρ d z = − ∂ A z ∂ ρ + ∂ A ρ ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }&=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\&={\frac {A_{z}(\rho )\,dz-A_{z}(\rho +d\rho )\,dz+A_{\rho }(z+dz)\,d\rho -A_{\rho }(z)\,d\rho }{d\rho \,dz}}\\&=-{\frac {\partial A_{z}}{\partial \rho }}+{\frac {\partial A_{\rho }}{\partial z}}\end{aligned}}}
( curl A ) z = lim S ⊥ z ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ρ ( ϕ ) d ρ − A ρ ( ϕ + d ϕ ) d ρ + A ϕ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ − A ϕ ( ρ ) ρ d ϕ ρ d ρ d ϕ = − 1 ρ ∂ A ρ ∂ ϕ + 1 ρ ∂ ( ρ A ϕ ) ∂ ρ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\hat {\boldsymbol {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\[1ex]&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\[1ex]&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}
curl A = ( curl A ) ρ ρ ^ + ( curl A ) ϕ ϕ ^ + ( curl A ) z z ^ = ( 1 ρ ∂ A z ∂ ϕ − ∂ A ϕ ∂ z ) ρ ^ + ( ∂ A ρ ∂ z − ∂ A z ∂ ρ ) ϕ ^ + 1 ρ ( ∂ ( ρ A ϕ ) ∂ ρ − ∂ A ρ ∂ ϕ ) z ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\[1ex]&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}
Spherical derivation [ edit ] div A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A r ( r + d r ) ( r + d r ) d θ ( r + d r ) sin θ d ϕ − A r ( r ) r d θ r sin θ d ϕ + A θ ( θ + d θ ) sin ( θ + d θ ) r d r d ϕ − A θ ( θ ) sin ( θ ) r d r d ϕ + A ϕ ( ϕ + d ϕ ) r d r d θ − A ϕ ( ϕ ) r d r d θ d r r d θ r sin θ d ϕ = 1 r 2 ∂ ( r 2 A r ) ∂ r + 1 r sin θ ∂ ( A θ sin θ ) ∂ θ + 1 r sin θ ∂ A ϕ ∂ ϕ {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{r}(r+dr)(r+dr)\,d\theta \,(r+dr)\sin \theta \,d\phi -A_{r}(r)r\,d\theta \,r\sin \theta \,d\phi +A_{\theta }(\theta +d\theta )\sin(\theta +d\theta )r\,dr\,d\phi -A_{\theta }(\theta )\sin(\theta )r\,dr\,d\phi +A_{\phi }(\phi +d\phi )r\,dr\,d\theta -A_{\phi }(\phi )r\,dr\,d\theta }{dr\,r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r^{2}}}{\frac {\partial (r^{2}A_{r})}{\partial r}}+{\frac {1}{r\sin \theta }}{\frac {\partial (A_{\theta }\sin \theta )}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}\end{aligned}}}
( curl A ) r = lim S ⊥ r ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A θ ( ϕ ) r d θ + A ϕ ( θ + d θ ) r sin ( θ + d θ ) d ϕ − A θ ( ϕ + d ϕ ) r d θ − A ϕ ( θ ) r sin ( θ ) d ϕ r d θ r sin θ d ϕ = 1 r sin θ ∂ ( A ϕ sin θ ) ∂ θ − 1 r sin θ ∂ A θ ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{r}=\lim _{S^{\perp {\boldsymbol {\hat {r}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\theta }(\phi )r\,d\theta +A_{\phi }(\theta +d\theta )r\sin(\theta +d\theta )\,d\phi -A_{\theta }(\phi +d\phi )r\,d\theta -A_{\phi }(\theta )r\sin(\theta )\,d\phi }{r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}\end{aligned}}}
( curl A ) θ = lim S ⊥ θ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( r ) r sin θ d ϕ + A r ( ϕ + d ϕ ) d r − A ϕ ( r + d r ) ( r + d r ) sin θ d ϕ − A r ( ϕ ) d r d r r sin θ d ϕ = 1 r sin θ ∂ A r ∂ ϕ − 1 r ∂ ( r A ϕ ) ∂ r {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\theta }=\lim _{S^{\perp {\boldsymbol {\hat {\theta }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\phi }(r)r\sin \theta \,d\phi +A_{r}(\phi +d\phi )\,dr-A_{\phi }(r+dr)(r+dr)\sin \theta \,d\phi -A_{r}(\phi )\,dr}{dr\,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {1}{r}}{\frac {\partial (rA_{\phi })}{\partial r}}\end{aligned}}}
( curl A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A r ( θ ) d r + A θ ( r + d r ) ( r + d r ) d θ − A r ( θ + d θ ) d r − A θ ( r ) r d θ r d r d θ = 1 r ∂ ( r A θ ) ∂ r − 1 r ∂ A r ∂ θ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{r}(\theta )\,dr+A_{\theta }(r+dr)(r+dr)\,d\theta -A_{r}(\theta +d\theta )\,dr-A_{\theta }(r)r\,d\theta }{r\,dr\,d\theta }}\\&={\frac {1}{r}}{\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}\end{aligned}}}
curl A = ( curl A ) r r ^ + ( curl A ) θ θ ^ + ( curl A ) ϕ ϕ ^ = 1 r sin θ ( ∂ ( A ϕ sin θ ) ∂ θ − ∂ A θ ∂ ϕ ) r ^ + 1 r ( 1 sin θ ∂ A r ∂ ϕ − ∂ ( r A ϕ ) ∂ r ) θ ^ + 1 r ( ∂ ( r A θ ) ∂ r − ∂ A r ∂ θ ) ϕ ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}\\[1ex]&={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}\end{aligned}}}
The unit vector of a coordinate parameter u is defined in such a way that a small positive change in u causes the position vector r {\displaystyle \mathbf {r} } u {\displaystyle \mathbf {u} }
Therefore, ∂ r ∂ u = ∂ s ∂ u u {\displaystyle {\frac {\partial {\mathbf {r} }}{\partial u}}={\frac {\partial {s}}{\partial u}}\mathbf {u} } s is the arc length parameter.
For two sets of coordinate systems u i {\displaystyle u_{i}} v j {\displaystyle v_{j}} chain rule , d r = ∑ i ∂ r ∂ u i d u i = ∑ i ∂ s ∂ u i u ^ i d u i = ∑ j ∂ s ∂ v j v ^ j d v j = ∑ j ∂ s ∂ v j v ^ j ∑ i ∂ v j ∂ u i d u i = ∑ i ∑ j ∂ s ∂ v j ∂ v j ∂ u i v ^ j d u i . {\displaystyle d\mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial u_{i}}}\,du_{i}=\sum _{i}{\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}du_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\,dv_{j}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\sum _{i}{\frac {\partial v_{j}}{\partial u_{i}}}\,du_{i}=\sum _{i}\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}\,du_{i}.}
Now, we isolate the i {\displaystyle i} th component. For i ≠ k {\displaystyle i{\neq }k} d u k = 0 {\displaystyle \mathrm {d} u_{k}=0} d u i {\displaystyle \mathrm {d} u_{i}} ∂ s ∂ u i u ^ i = ∑ j ∂ s ∂ v j ∂ v j ∂ u i v ^ j . {\displaystyle {\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}.}
![{\displaystyle \theta \in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c833964ea08aa30df8b6f56664461a5499b38144)
![{\displaystyle \varphi \in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adacea8b18fa91c9b01816ed054d2cf4f26b72fb)


















































![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3116bd7e75151c8d599b5e090d2433daffa21069)
![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89522d9531233ee5f0a581ec441bb20c337a13b8)




















![{\displaystyle \nabla ^{2}\left(\mathbf {P} \cdot \mathbf {Q} \right)=\mathbf {Q} \cdot \nabla ^{2}\mathbf {P} -\mathbf {P} \cdot \nabla ^{2}\mathbf {Q} +2\nabla \cdot \left[\left(\mathbf {P} \cdot \nabla \right)\mathbf {Q} +\mathbf {P} \times \nabla \times \mathbf {Q} \right]\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e39d7e00d51ce89633c61a8f5939819f39e8e8d8)






![{\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\hat {\boldsymbol {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\[1ex]&={\frac {A_{\phi }(z)\left(\rho +d\rho \right)\,d\phi -A_{\phi }(z+dz)\left(\rho +d\rho \right)\,d\phi +A_{z}(\phi +d\phi )\,dz-A_{z}(\phi )\,dz}{\left(\rho +d\rho \right)\,d\phi \,dz}}\\[1ex]&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8649ecbfebe77589420c030858b59022fe882071)

![{\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\hat {\boldsymbol {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\[1ex]&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\[1ex]&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1728c015b8b117cd7a8229bb3735923203173ee)
![{\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\[1ex]&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77b80d1002f75cfccc65fc1978533b2438fcd647)




![{\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}\\[1ex]&={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d78f6369c32fc51bf5fa7d789aa7ded169e027)










