Конструкции в гиперболической геометрии.
Гиперболическая геометрия — это неевклидова геометрия первые четыре аксиомы евклидовой геометрии, , в которой сохраняются пятая аксиома — постулат параллельности но изменяется . Пятая аксиома гиперболической геометрии гласит, что если задана прямая L и точка P проходят как минимум две прямые не лежащая на этой прямой, то через P , параллельные L. , [1] Как и в евклидовой геометрии, где древнегреческие математики использовали циркуль и идеализированную линейку для построения длин, углов и других геометрических фигур, в гиперболической геометрии также могут быть построены конструкции.
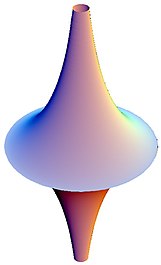
Модели гиперболической геометрии
[ редактировать ]Существует несколько моделей гиперболической геометрии, которые могут упростить выполнение и визуализацию построений. Части гиперболической плоскости можно поместить на псевдосферу и сохранить углы и гиперболические расстояния, а также изогнуться вокруг псевдосферы, сохраняя при этом ее свойства. [2] Однако на псевдосферу в качестве модели можно поместить не всю гиперболическую плоскость, а только часть гиперболической плоскости. [2]

Всю гиперболическую плоскость также можно поместить на диск Пуанкаре и сохранить ее углы. Однако линии превратятся в круговые дуги, что их исказит. [2]
Инструменты
[ редактировать ]В гиперболической геометрии можно использовать стандартную линейку и циркуль, которые часто используются в евклидовой плоской геометрии . Однако существуют разнообразные циркули и линейки, разработанные для гиперболических построений.
Гиперкомпас по можно использовать для построения гиперцикла центральной линии и радиусу. [3] Горокомпас через определенную точку , можно использовать для построения орицикла если также указаны диаметр и направление. Оба из них также требуют прямой кромки, как у стандартной линейки . [3] При построении гиперболической геометрии, если вы используете подходящую линейку для построения, все три циркуля (то есть горокомпас, гиперкомпас и стандартный компас ) могут выполнять одни и те же построения. [3]
можно С помощью параллельной линейки провести линию, проходящую через данную точку А и параллельную данному лучу а. [3] . Для любых двух линий можно использовать гиперболическую линейку , чтобы построить линию, параллельную первой линии и перпендикулярную второй. [3]
Несколько замечаний по использованию линеек:
- С помощью параллельной линейки можно построить все, что можно построить с помощью стандартной линейки и трех циркулей. [3]
- Параллельная линейка может действовать как линейка в евклидовой геометрии. [3]
- Гиперболическая линейка не может выполнять построения евклидовой геометрии. [3]
- В гиперболической геометрии построения, которые можно выполнить с помощью любого из трех перечисленных выше циркуля и параллельной линейки, можно выполнить и с помощью гиперболической линейки. [3]
Простые конструкции
[ редактировать ]Биссектриса угла
[ редактировать ]Рассмотрим заданный угол ᗉ IAI' ≠ π /2 радиан, биссектрису которого ищем. Это приводит к двум различным случаям: либо ᗉ IAI' < π /2 радиан, либо ᗉ IAI' > π /2 радиан. [3] В обоих случаях необходима гиперболическая линейка, чтобы построить линию BI', где BI' перпендикулярна AI и параллельна AI'. Также постройте линию B'I, где B'I перпендикулярен AI' и параллелен AI. [3]
Случай 1: ᗉ IAI'< π /2 радиан
Пусть C — пересечение BI' и B'I. В результате линия AC делит пополам ᗉ IAI'. [3]

Случай 2: ᗉ IAI' > π /2 радиан
Этот случай далее разбивается на три подслучая:
- Случай 2а: IB' пересекает I'B
- Пусть А' — пересечение IB' и I'B. Тогда AA' — биссектриса угла ᗉ IAI'. [3]
- Случай 2б: IB' параллелен I'B.
- Постройте отрезок BB' и с помощью гиперболической линейки постройте линию OI" так, чтобы OI" была перпендикулярна BB' и параллельна BI". Тогда линия OA является биссектрисой угла ᗉ IAI'. [3]
- Случай 2в: IB' ультрапараллелен I'B.
- Используя теорему об ультрапараллели , постройте общий перпендикуляр к IB' и I'B, CC'. Пусть пересечение CB" и BC' будет D. В результате AD будет биссектрисой ᗉ BDB'. Затем мы обнаружим, что линия, проходящая через OD, также является биссектрисой ᗉ IAI'. [3]
Общая параллельная линия двух линий
[ редактировать ]Рассмотрим задачу нахождения прямой, параллельной двум заданным прямым a и a' . Возможны три случая: а и а' пересекаются в точке О, а и а' параллельны друг другу, а и а ' ультрапараллельны друг другу. [3]
Случай 1: а и а' пересекаются в точке О,
Разделите пополам один из углов, образованных этими двумя прямыми, и назовите биссектрису b . Используя гиперболическую линейку, постройте прямую c так, чтобы c была перпендикулярна b и параллельна a. В результате c также параллельна a', что делает c общей параллелью прямым a и a'. [3]
Случай 2: a и a' параллельны друг другу.
Используя гиперболическую линейку, постройте AI' так, чтобы AI' был параллелен a' и перпендикулярен a. Постройте другую прямую A'I так, чтобы A'I была параллельна a и перпендикулярна a'. Пусть пересечение AI' и A'I будет B. Поскольку ᗉ IBI' > π /2 радиан , случай теперь разыгрывается как случай 1, что позволяет построить общую параллель с BI и BI'. [3]
Случай 3: a и a' ультрапараллельны друг другу.
Используя гиперболическую линейку, постройте BI' так, чтобы BI' был перпендикулярен a и параллелен a' , и постройте линию B'I так, чтобы B'I был перпендикулярен a' и параллелен a таким образом, чтобы BI' и была параллельна a'. B'I находится по одну сторону от общего перпендикуляра к a и a', который можно найти с помощью теоремы об ультрапараллели . Пусть пересечение BI' и B'I будет C. Тогда ᗉ ICI' ≠ π /2 радиан, что позволяет закончить построение аналогично двум другим случаям. [3]
Линия, перпендикулярная другой прямой в точке
[ редактировать ]Предположим, у вас есть линия a и точка A на этой прямой, и вы хотите построить линию, перпендикулярную a и проходящую через A. Тогда пусть a' будет линией, проходящей через A, где a и a' — две разные прямые. Тогда у вас будет один из двух случаев. [3]
Случай 1: а перпендикулярно а'
В этом случае у нас уже есть линия, перпендикулярная a , проходящая через A. [3]
Случай 2: a и a' не перпендикулярны друг другу.
Используя гиперболическую линейку, постройте линию BI так, чтобы BI была перпендикулярна a и параллельна a'. Также постройте линию CI' так, чтобы CI' была перпендикулярна a и параллельна a', но в противоположном направлении от BI. Теперь проведите линию II" так, чтобы II" была общей параллелью BI и I'C. Теорема об ультрапараллели теперь позволяет нам создать общий перпендикуляр к II" и а, поскольку эти две прямые ультрапараллельны. Этот общий перпендикуляр теперь является линией, перпендикулярной к а и проходящей через А. [3]
Средняя точка отрезка
[ редактировать ]Предположим, вы пытаетесь найти середину отрезка AB. Затем постройте линию AI так, чтобы AI проходила через точку A и была перпендикулярна AB. Также постройте линию BI' так, чтобы BI' пересекала AB в точке B и была перпендикулярна AB. Теперь постройте линию II' так, чтобы II' была общей параллелью AI и BI'. [3] Постройте общий перпендикуляр к II' и AB, что можно сделать с помощью теоремы об ультрапараллели, поскольку II' и AB ультрапараллельны друг другу. Назовите эту строку CC'. Теперь C оказывается серединой AB. [3]
Определения для сложных конструкций
[ редактировать ]
Для целей следующих определений будут сделаны следующие предположения, которые обычно не могут быть сделаны в гиперболической геометрии.
- Три отдельные точки создают уникальный круг [4]
- Учитывая любые две прямые, они встречаются в единственной точке. [4] (обычно это противоречило бы аксиоме параллельности гиперболической геометрии, поскольку может быть много разных прямых, параллельных одной и той же прямой). [1] )
- Угловые меры имеют знаки. Здесь они будут определены следующим образом: Рассмотрим треугольник XYZ. Знак угла ᗉ XYZ положителен тогда и только тогда, когда направление пути по кратчайшей дуге от стороны XY к стороне YZ направлено против часовой стрелки. Изображение треугольника справа описывает это. Для сравнения: при работе с единичным кругом величина угла положительна при движении против часовой стрелки и отрицательна при движении по часовой стрелке. [4]
Циклические четырехугольники
[ редактировать ]Четырехугольник называется вписанным, если сумма двух противоположных вершин равна пи радианам или 180 градусам. [4] Кроме того, если четырехугольник вписан в окружность так, что все его вершины лежат на окружности, он является вписанным. [5]
Псевдовысоты
[ редактировать ]Рассмотрим треугольник ABC, в котором точки отмечены по часовой стрелке, поэтому все углы положительны. Пусть X — точка, движущаяся по BC от B к C. По мере приближения X к C угол ᗉAXB будет уменьшаться, а угол ᗉ AXC увеличиваться. Когда X находится достаточно близко к B, ᗉ AXB > ᗉ AXC. Когда X достаточно близко к C, ᗉ AXB < ᗉ AXC. Это означает, что в какой-то момент X окажется в положении, где ᗉ AXB = ᗉ AXC. Когда X находится в этом положении, он определяется как основание псевдовысоты от вершины A. [4] Тогда псевдовысотой будет отрезок AX. [4]

Псевдодлины
[ редактировать ]Пусть d E (A,B) обозначает псевдодлину данного гиперболического отрезка AB. Пусть преобразование переместит A в центр диска Пуанкаре радиуса, равного 1. Псевдодлина d E (A,B) — это длина этого отрезка в евклидовой геометрии. [4]
Гомотетия
[ редактировать ]Учитывая точку P, точку A, где A является центром гомотетии, и число k, которое представляет отношение гомотетии, гомотетия представляет собой преобразование, которое переместит P в точку P', где P' находится на луче. AP и dE ( A,P') = k·d E (A,P). [4]
Теорема о трех дураках
[ редактировать ]Рассмотрим три окружности ω 1 , ω 2 и ω 3 в общей плоскости. Пусть P 1 будет пересечением двух внешних касательных линий ω 2 и ω 3 . Пусть P 2 и P 3 находятся одинаково. Теорема о трёх колпаках утверждает, что P1 , P2 и P3 лежат на одной прямой. [4]
Доказательство: постройте сферу поверх каждого круга, а затем постройте плоскость, касательную к этим трем сферам. Плоскость пересекает плоскость, на которой лежат окружности, по прямой, содержащей P1 , P2 и P3 . Эти точки также являются центрами гомотетии окружностей, из которых они произошли. [4]
Применение к сферической геометрии
[ редактировать ]Алгебраически гиперболическая и сферическая геометрия имеют одинаковую структуру. [4] Это позволяет нам применять концепции и теоремы из одной геометрии к другой. [4] Применение гиперболической геометрии к сферической геометрии может облегчить понимание, поскольку сферы гораздо более конкретны, что облегчает концептуализацию сферической геометрии.
Ссылки
[ редактировать ]- ↑ Перейти обратно: Перейти обратно: а б Кэннон, Джеймс В.; Флойд, Уильям Дж.; Кеньон, Ричард; Перри, Уолтер Р. (1997). «Гиперболическая геометрия» (PDF) . библиотека.msri.org . Проверено 13 декабря 2018 г.
- ↑ Перейти обратно: Перейти обратно: а б с Роте, Франц (7 сентября 2006 г.). «Гиперболическая геометрия и псевдосфера» (PDF) . math2.uncc.edu . Архивировано из оригинала (PDF) 9 января 2018 г. Проверено 13 декабря 2018 г.
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час я дж к л м н тот п д р с т в v В х Аль-Дахир, М.В. (1962). «Прибор в гиперболической геометрии» . Труды Американского математического общества . 13 (2): 298–304. дои : 10.1090/S0002-9939-1962-0138036-7 . JSTOR 2034487 .
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час я дж к л Акопян, Арсений В. (11 мая 2011 г.). «О некоторых классических конструкциях, распространенных на гиперболическую геометрию». arXiv : 1105.2153 [ math.MG ].
- ^ Леонард, И. Эд; Льюис, Дж. Э.; Лю, ACF; Токарский, Г.В. (4 июня 2014 г.). Классическая геометрия: евклидова, трансформационная, инверсивная и проективная . Хобокен, Нью-Джерси. ISBN 9781118839430 . OCLC 861966488 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )