Граф (дискретная математика)

В дискретной математике , а точнее в теории графов , граф — это структура, состоящая из набора объектов, в котором некоторые пары объектов в некотором смысле «связаны». Объекты представлены абстракциями, называемыми вершинами (также называемыми узлами или точками ), и каждая из связанных пар вершин называется ребром ( также называемым ссылкой или линией ). ^[1] Обычно граф изображается в схематической форме в виде набора точек или кружков для вершин, соединенных линиями или кривыми для ребер.

Края могут быть направленными и ненаправленными. Например, если вершины представляют людей на вечеринке, и между двумя людьми, если они пожимают друг другу руки, есть ребро, то этот граф является неориентированным, поскольку любой человек A может пожать руку человеку B только в том случае, если B также пожимает руку A . Напротив, если ребро от человека A к человеку B означает, что A должен деньги B , тогда этот граф является направленным, поскольку задолженность по деньгам не обязательно является взаимной.

Графы — основной предмет, изучаемый теорией графов. Слово «график» впервые было использовано в этом смысле Дж. Дж. Сильвестром в 1878 году из-за прямой связи между математикой и химической структурой (то, что он назвал химико-графическим изображением). ^[2]^[3]

Определения [ править ]

Определения в теории графов различаются. Ниже приведены некоторые из наиболее основных способов определения графиков и связанных с ними математических структур .

График [ править ]

Граф чтобы (иногда называемый неориентированным графом, отличить его от ориентированного графа , или простым графом, чтобы отличить его от мультиграфа ) ^[4]^[5] — пара $G = (V, E)$ , где $V$ — набор, элементы которого называются вершинами (единственное число: вершина), а $E$ — набор неупорядоченных пар. $\{v_{1},v_{2}\}$ вершин, элементы которых называются ребрами (иногда звеньями или линиями ).

Вершины $u$ и $v$ ребра ${u, v}$ ребра называются конечными точками . Говорят, что ребро соединяет $u$ и $v$ и инцидентно им . Вершина не может принадлежать ни одному ребру; в этом случае она не соединяется ни с одной другой вершиной и называется изолированной . Когда край $\{u,v\}$ существует, вершины $u$ и $v$ называются смежными .

Мультиграф — это обобщение, позволяющее нескольким ребрам иметь одну и ту же пару конечных точек. В некоторых текстах мультиграфы называют просто графами. ^[6]^[7]

Иногда графам разрешается содержать петли — ребра, соединяющие вершину с самой собой. Чтобы разрешить циклы, парам вершин в $E$ должно быть разрешено иметь один и тот же узел дважды. Такие обобщенные графы называются графами с петлями или просто графами, если из контекста ясно, что петли разрешены.

Обычно множество вершин $V$ считается конечным (что означает, что множество ребер $E$ также конечно). Иногда бесконечные графы рассматривают , но обычно их рассматривают как особый вид бинарных отношений , поскольку большинство результатов о конечных графах либо не распространяются на бесконечный случай, либо требуют совсем иного доказательства.

Пустой граф — это граф, имеющий пустое множество вершин (и, следовательно, пустое множество ребер). Порядок номер графа — это его $| В |$ вершин, обычно обозначаемых $n$ . Размер номер графа — это его $| Е |$ ребер, обычно обозначаемых $m$ . Однако в некоторых контекстах, например для выражения вычислительной сложности алгоритмов, термин «размер» используется для обозначения величины $| В | + | Е |$ (в противном случае непустой граф мог бы иметь размер 0). Степень валентность или ; вершины — это количество инцидентных ей ребер для графов с циклами цикл учитывается дважды.

В графе порядка $n$ максимальная степень каждой вершины равна $n - 1$ (или $n + 1$ , если циклы разрешены, поскольку цикл вносит 2 в степень), а максимальное количество ребер равно $n (n - 1). /2$ (или $n (n + 1)/2,$ если циклы разрешены).

Ребра графа определяют симметричное отношение на вершинах, называемое отношением смежности . В частности, две вершины $x$ и $y$ являются смежными, если ${x, y}$ является ребром. Граф полностью определяется своей матрицей смежности $A$ , которая представляет собой $квадратную матрицу размера n \times n$ , где $A ij$ определяет количество соединений от вершины $i$ к вершине $j$ . Для простого графа $A ij$ равен либо 0, что указывает на разъединение, либо 1, что указывает на соединение; более того, $A ii = 0$ , поскольку ребро в простом графе не может начинаться и заканчиваться в одной и той же вершине. Графы с циклами будут характеризоваться тем, что некоторые или все $A ii$ равны положительному целому числу, а мультиграфы (с несколькими ребрами между вершинами) будут характеризоваться тем, что некоторые или все $A ij$ равны положительному целому числу. Неориентированные графы будут иметь симметричную матрицу смежности (что означает $A ij = A ji$ ).

Ориентированный граф [ править ]

Ориентированный граф с тремя вершинами и четырьмя направленными ребрами (двойная стрелка обозначает ребро в каждом направлении).

или Ориентированный граф орграф — это граф, в котором ребра имеют ориентацию.

В одном ограниченном, но очень распространенном смысле этого термина: ^[8] — ориентированный граф это пара $G = (V, E),$ содержащая:

$V$ — набор вершин узлами (также называемых или точками ) ;
$E$ — набор ребер , (также называемых направленными ребрами направленными связями , направленными линиями , стрелками или дугами ), которые представляют собой упорядоченные пары различных вершин: $E\subseteq \{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}$ .

Во избежание двусмысленности объект такого типа можно назвать именно ориентированным простым графом .

В ребре $(x, y),$ направленном от $x$ к $y$ , вершины $x$ и $y$ называются концами ребра, $x -$ ребра хвостом и $y$ ребра - головой . Говорят, что соединяет $x$ и $y$ и инцидентно ребро $x$ и $y$ . Вершина может существовать в графе и не принадлежать ребру. Ребро $(y, x)$ называется перевернутым ребром $(x, y)$ . Множественные ребра , недопустимые согласно приведенному выше определению, представляют собой два или более ребер с одинаковым хвостом и одной и той же головкой.

В более общем смысле термина, допускающего наличие нескольких ребер, ^[8] ориентированный граф иногда определяется как упорядоченная тройка $G = (V, E, φ),$ содержащая:

$V$ — набор вершин узлами (также называемых или точками ) ;
$E$ , набор ребер , (также называемых направленными ребрами направленными связями , направленными линиями , стрелками или дугами );
$φ$ , функция инцидентности , отображающая каждое ребро в упорядоченную пару вершин (т. е. ребро связано с двумя различными вершинами): $\phi :E\to \{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}$ .

Во избежание двусмысленности объект такого типа можно назвать именно ориентированным мультиграфом .

Петля — это ребро, которое соединяет вершину с самой собой. Ориентированные графы, определенные в двух определениях выше, не могут иметь петель, потому что петля, соединяющая вершину $x$ самому себе является ребром (для ориентированного простого графа) или инцидентно (для ориентированного мультиграфа) $(x,x)$ которого нет в $\{(x,y)\mid (x,y)\in V^{2}\;{\textrm {and}}\;x\neq y\}$ . Поэтому, чтобы разрешить циклы, определения должны быть расширены. Для ориентированных простых графов определение $E$ следует изменить на $E\subseteq \{(x,y)\mid (x,y)\in V^{2}\}$ . Для ориентированных мультиграфов определение $\phi$ следует изменить на $\phi :E\to \{(x,y)\mid (x,y)\in V^{2}\}$ . Чтобы избежать двусмысленности, эти типы объектов можно назвать именно ориентированным простым графом, допускающим циклы , и ориентированным мультиграфом, допускающим циклы (или колчаном ) соответственно.

Ребра ориентированного простого графа, допускающие петли $G,$ собой однородное отношение С на вершинах графа $G$ , называемое отношением смежности графа $G.$ представляют В частности, для каждого ребра $(x, y)$ его конечные точки $x$ и $y$ считаются смежными друг с другом, что обозначается $x ~ y$ .

Смешанный график [ править ]

— Смешанный граф это граф, в котором некоторые ребра могут быть направленными, а некоторые — ненаправленными. Это упорядоченная тройка $G = (V, E, A)$ для смешанного простого графа и $G = (V, E, A, φ E, φ A)$ для смешанного мультиграфа с $V$ , $E$ (неориентированными ребрами), $A$ (направленные ребра), $φ E$ и $φ A,$ определенные выше. Ориентированные и неориентированные графы являются особыми случаями.

Взвешенный график [ править ]

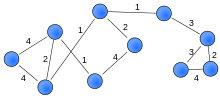
граф Взвешенный или сеть ^[9]^[10] — это граф, в котором каждому ребру присвоен номер (вес). ^[11] Такие веса могут представлять, например, стоимость, длину или мощность, в зависимости от решаемой проблемы. Такие графы возникают во многих контекстах, например, в задачах о кратчайшем пути, таких как задача коммивояжера .

Типы графиков [ править ]

Ориентированный граф [ править ]

Одно из определений ориентированного графа состоит в том, что это ориентированный граф, в котором не более одного из ( x , y ) и ( y , x ) может быть ребром графа. То есть это ориентированный граф, который можно сформировать как ориентацию неориентированного (простого) графа.

Некоторые авторы используют термин «ориентированный граф» для обозначения того же, что и «ориентированный граф». Некоторые авторы используют термин «ориентированный граф» для обозначения любой ориентации данного неориентированного графа или мультиграфа.

Обычный график [ править ]

— Правильный граф это граф, в котором каждая вершина имеет одинаковое количество соседей, т. е. каждая вершина имеет одинаковую степень. Регулярный граф с вершинами степени k называется k -регулярным графом или регулярным графом степени k .

Полный график [ править ]

— Полный граф это граф, в котором каждая пара вершин соединена ребром. Полный граф содержит все возможные ребра.

Конечный граф [ править ]

Конечный граф — это граф, в котором множество вершин и множество ребер являются конечными множествами . В противном случае его называют бесконечным графом .

Чаще всего в теории графов подразумевается, что обсуждаемые графы конечны. Если графы бесконечны, это обычно специально оговаривается.

Связный граф [ править ]

В неориентированном графе неупорядоченная пара вершин { x , y } называется связной , если путь ведет от x к y . В противном случае неупорядоченная пара называется несвязной .

— Связный граф это неориентированный граф, в котором каждая неупорядоченная пара вершин графа связна. В противном случае его называют несвязным графом .

В ориентированном графе упорядоченная пара вершин ( x , y ) называется сильно связной , если направленный путь ведет от x к y . В противном случае упорядоченная пара называется слабосвязной , если ненаправленный путь ведет от x к y после замены всех ее направленных ребер ненаправленными. В противном случае упорядоченная пара называется несвязной .

— Сильно связный граф это ориентированный граф, в котором каждая упорядоченная пара вершин графа сильно связна. В противном случае граф называется слабо связным, если каждая упорядоченная пара вершин графа слабо связна. В противном случае его называют несвязным графом .

Граф с k-вершиной связности или граф с k-связностью ребер — это граф, в котором не существует набора из k - 1 вершин (соответственно ребер), удаление которых разъединяет граф. Граф с k -связностью часто называют просто k-связным графом .

Двудольный граф [ править ]

Двудольный граф — это простой граф, в котором множество вершин можно разделить на два множества, W и X , так что никакие две вершины в W не имеют общего ребра и никакие две вершины в X не имеют общего ребра. Альтернативно, это граф с хроматическим числом 2.

В полном двудольном графе множество вершин представляет собой объединение двух непересекающихся множеств, W и X , так что каждая вершина в W смежна с каждой вершиной в X, нет ребер но внутри W или X .

Граф пути [ править ]

Граф путей или линейный граф порядка n ≥ 2 — это граф, в котором вершины могут быть перечислены в порядке v ₁ , v ₂ , …, v _n так, что ребрами являются { v _i , v _{i +1} } , где i = 1, 2, …, n − 1. Графы путей можно охарактеризовать как связные графы, в которых степень всех вершин, кроме двух, равна 2, а степень двух оставшихся вершин равна 1. Если граф путей встречается как подграф другого графа, это путь в этом графе.

Планарный граф [ править ]

Планарный граф — это граф, вершины и ребра которого можно нарисовать на плоскости так, что никакие два ребра не пересекаются.

График цикла [ править ]

Граф циклов или круговой граф порядка n ≥ 3 — это граф, в котором вершины могут быть перечислены в порядке v ₁ , v ₂ , …, v _n так, что ребрами являются { v _i , v _{i +1} } , где я знак равно 1, 2, …, n - 1, плюс ребро { v _n , v ₁ } . Графы циклов можно охарактеризовать как связные графы, в которых степень всех вершин равна 2. Если граф циклов встречается как подграф другого графа, он является циклом или схемой в этом графе.

Дерево [ править ]

Дерево связный — это неориентированный граф, в котором любые две вершины соединены ровно одним путем , или, что то же самое, ациклический неориентированный граф.

Лес — это неориентированный граф , в котором любые две вершины соединены не более чем одним путем, или, что то же самое, ациклический неориентированный граф или, что то же самое, непересекающееся объединение деревьев.

Политри [ править ]

Полидерево , (или ориентированное дерево , или ориентированное дерево или односвязная сеть ) — это ориентированный ациклический граф (DAG), базовым неориентированным графом которого является дерево.

Полилес ) — это ориентированный ациклический граф , (или направленный лес или ориентированный лес базовым неориентированным графом которого является лес.

Продвинутые классы [ править ]

Более продвинутые виды графиков:

граф Петерсена и его обобщения;
идеальные графики ;
кографы ;
хордальные графы ;
другие графы с большими группами автоморфизмов : вершинно-транзитивные , дуготранзитивные и дистанционно-транзитивные графы ;
сильно регулярные графы и их обобщения, дистанционно регулярные графы .

Свойства графиков [ править ]

Два ребра графа называются смежными, если они имеют общую вершину. Два ребра ориентированного графа называются последовательными, если голова первого является хвостом второго. Аналогично, две вершины называются смежными, если они имеют общее ребро ( последовательными , если первая вершина является хвостом, а вторая — головой ребра), и в этом случае говорят, что общее ребро соединяет две вершины. Ребро и вершина на этом ребре называются инцидентными .

Граф, имеющий только одну вершину и не имеющий ребер, называется тривиальным графом . Граф, имеющий только вершины и не имеющий ребер, называется графом без ребер . Граф без вершин и ребер иногда называют нулевым графом или пустым графом , но терминология непоследовательна, и не все математики допускают этот объект.

Обычно вершины графа по своей природе как элементы множества различимы. Этот вид графа можно назвать помеченным вершинами . Однако во многих вопросах лучше считать вершины неразличимыми. (Конечно, вершины еще можно различать по свойствам самого графа, например, по количеству инцидентных ребер.) Те же замечания применимы и к ребрам, поэтому графы с помеченными ребрами называются помеченными ребрами . Графы с метками, прикрепленными к ребрам или вершинам, обычно называются помеченными . Следовательно, графы, в которых вершины неразличимы, а ребра неразличимы, называются неразмеченными . (В литературе термин «размеченный» может применяться к другим видам разметки, помимо того, который служит только для различения разных вершин или ребер.)

Категория категория всех графов — это с запятой Set ↓ D , где D : Set → Set — это функтор, переводящий набор s в s × s .

Примеры [ править ]

Диаграмма представляет собой схематическое изображение графа с вершинами $V=\{1,2,3,4,5,6\}$ и края $E=\{\{1,2\},\{1,5\},\{2,3\},\{2,5\},\{3,4\},\{4,5\},\{4,6\}\}.$
В информатике ориентированные графы используются для представления знаний (например, концептуальный граф ), конечных автоматов и многих других дискретных структур.
Бинарное отношение R на множестве X определяет ориентированный граф. Элемент x из X является прямым предшественником элемента y из X тогда и только тогда, когда xRy .
Ориентированный граф может моделировать информационные сети, такие как Twitter , где один пользователь следует за другим. ^[12]^[13]
Особенно регулярные примеры ориентированных графов дают графы Кэли конечно порожденных групп, а также смежные графы Шрайера.
В теории категорий каждая маленькая категория имеет направленный мультиграф, вершины которого являются объектами категории, а ребра — стрелками категории. На языке теории категорий говорят, что существует забывчивый функтор из категории малых категорий в категорию колчанов .

Операции с графами [ править ]

Существует несколько операций, которые создают новые графы из исходных, которые можно разделить на следующие категории:

унарные операции , которые создают новый граф из исходного, например:
бинарные операции , которые создают новый граф из двух исходных, например:

Обобщения [ править ]

В гиперграфе ребро может соединять любое положительное количество вершин.

Неориентированный граф можно рассматривать как симплициальный комплекс, состоящий из 1- симплексов (ребер) и 0-симплексов (вершин). По сути, комплексы являются обобщением графов, поскольку они допускают симплексы более высокой размерности.

Каждый граф порождает матроид .

В теории моделей граф — это просто структура . Но в таком случае ограничений на количество ребер нет: это может быть любое кардинальное число , см. непрерывный граф .

В вычислительной биологии анализ степенных графов представляет степенные графы как альтернативное представление неориентированных графов.

В географических информационных системах геометрические сети моделируются по образцу графов и заимствуют многие концепции из теории графов для выполнения пространственного анализа дорожных сетей или инженерных сетей.

См. также [ править ]

Примечания [ править ]

^ Трюдо, Ричард Дж. (1993). Введение в теорию графов (Исправленное, расширенное издание. Под ред.). Нью-Йорк: Паб Dover. п. 19. ISBN 978-0-486-67870-2 . Архивировано из оригинала 5 мая 2019 года . Проверено 8 августа 2012 г. Граф — это объект, состоящий из двух наборов, называемых набором вершин и набором ребер .
^
См.:
- Джей Джей Сильвестр (7 февраля 1878 г.) «Химия и алгебра» , архивировано 4 февраля 2023 г. в Wayback Machine Nature , 17 : 284. дои : 10.1038/017284a0 . Со страницы 284: «Таким образом, каждый инвариант и ковариант становится выражаемым посредством графика, точно идентичного диаграмме Кекуле или химикографу».
- Дж. Дж. Сильвестр (1878 г.) «О применении новой атомной теории к графическому представлению инвариантов и ковариантов бинарных квантов – с тремя приложениями» , Архивировано 2023 г. в 4 февраля Американском журнале математики, чистой и Применено , 1 (1): 64–90. дои : 10.2307/2369436 . JSTOR 2369436 . Термин «график» впервые появляется в этой статье на странице 65.
^ Гросс, Джонатан Л.; Йеллен, Джей (2004). Справочник по теории графов . ЦРК Пресс . п. 35 . ISBN 978-1-58488-090-5 . Архивировано из оригинала 4 февраля 2023 г. Проверено 16 февраля 2016 г.
^ Бендер и Уильямсон 2010 , с. 148.
↑ См., например, Иянага и Кавада, 69 J , с. 234 или Биггс, с. 4.
^ Бендер и Уильямсон 2010 , с. 149.
^ Грэм и др., стр. 5.
^ Jump up to: ^а ^б Бендер и Уильямсон 2010 , с. 161.
^ Стрэнг, Гилберт (2005), Линейная алгебра и ее приложения (4-е изд.), Брукс Коул, ISBN 978-0-03-010567-8
^ Льюис, Джон (2013), Структуры программного обеспечения Java (4-е изд.), Пирсон, стр. 405, ISBN 978-0133250121
^ Флетчер, Питер; Хойл, Хьюз; Пэтти, К. Уэйн (1991). Основы дискретной математики (под ред. международного студента). Бостон: Паб PWS-KENT. Компания р. 463. ИСБН 978-0-53492-373-0 . — Взвешенный граф число w ( e ), называемое его весом присвоено это граф, в котором каждому ребру e .
^ Гранжан, Мартин (2016). «Анализ социальной сети Twitter: составление карты сообщества цифровых гуманитарных наук» . Cogent Искусства и Гуманитарные науки . 3 (1): 1171458. doi : 10.1080/23311983.2016.1171458 . Архивировано из оригинала 02 марта 2021 г. Проверено 16 сентября 2019 г.
↑ Панкадж Гупта, Ашиш Гоэл, Джимми Лин, Аниш Шарма, Донг Ван и Реза Босаг Заде WTF: Система «за кем следить» в Твиттере. Архивировано 12 июля 2019 г. в Wayback Machine , Материалы 22-й международной конференции по миру. Широкая сеть . дои : 10.1145/2488388.2488433 .

Ссылки [ править ]

Балакришнан, В.К. (1997). Теория графов (1-е изд.). МакГроу-Хилл. ISBN 978-0-07-005489-9 .
Банг-Дженсен, Дж.; Гутин, Г. (2000). Орграфы: теория, алгоритмы и приложения . Спрингер.
Бендер, Эдвард А.; Уильямсон, С. Гилл (2010). Списки, решения и графики. С введением в вероятность .
Берже, Клод (1958). Теория графов и ее приложения (на французском языке). Париж: Дюнод.
Биггс, Норман (1993). Алгебраическая теория графов (2-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-45897-9 .
Боллобас, Бела (2002). Современная теория графов (1-е изд.). Спрингер. ISBN 978-0-387-98488-9 .
Дистель, Рейнхард (2005). Теория графов (3-е изд.). Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-3-540-26183-4 .
Грэм, РЛ; Гретшель, М.; Ловас, Л. (1995). Справочник по комбинаторике . МТИ Пресс. ISBN 978-0-262-07169-7 .
Гросс, Джонатан Л.; Йеллен, Джей (1998). Теория графов и ее приложения . ЦРК Пресс. ISBN 978-0-8493-3982-0 .
Гросс, Джонатан Л.; Йеллен, Джей (2003). Справочник по теории графов . КПР. ISBN 978-1-58488-090-5 .
Харари, Фрэнк (1995). Теория графов . Издательство Аддисон Уэсли. ISBN 978-0-201-41033-4 .
Иянага, Сёкити; Кавада, Юкиёси (1977). Энциклопедический словарь математики . МТИ Пресс. ISBN 978-0-262-09016-2 .
Цвиллингер, Дэниел (2002). Стандартные математические таблицы и формулы CRC (31-е изд.). Чепмен и Холл/CRC. ISBN 978-1-58488-291-6 .

Дальнейшее чтение [ править ]

Трюдо, Ричард Дж. (1993). Введение в теорию графов (Исправленное, расширенное издание. Под ред.). Нью-Йорк: Dover Publications . ISBN 978-0-486-67870-2 . Проверено 8 августа 2012 г.

Внешние ссылки [ править ]

Ресурсы библиотеки о
Граф (математика)

Ресурсы в вашей библиотеке

СМИ, связанные с графиком (дискретная математика) на Викискладе?
Вайсштейн, Эрик В. «График» . Математический мир .

[:0-1] Трюдо, Ричард Дж. (1993). Введение в теорию графов (Исправленное, расширенное издание. Под ред.). Нью-Йорк: Паб Dover. п. 19. ISBN 978-0-486-67870-2 . Архивировано из оригинала 5 мая 2019 года . Проверено 8 августа 2012 г. Граф — это объект, состоящий из двух наборов, называемых набором вершин и набором ребер .

[2] См.:
Джей Джей Сильвестр (7 февраля 1878 г.) «Химия и алгебра» , архивировано 4 февраля 2023 г. в Wayback Machine Nature , 17 : 284. дои : 10.1038/017284a0 . Со страницы 284: «Таким образом, каждый инвариант и ковариант становится выражаемым посредством графика, точно идентичного диаграмме Кекуле или химикографу».
Дж. Дж. Сильвестр (1878 г.) «О применении новой атомной теории к графическому представлению инвариантов и ковариантов бинарных квантов – с тремя приложениями» , Архивировано 2023 г. в 4 февраля Американском журнале математики, чистой и Применено , 1 (1): 64–90. дои : 10.2307/2369436 . JSTOR 2369436 . Термин «график» впервые появляется в этой статье на странице 65.

[3] Джей Джей Сильвестр (7 февраля 1878 г.) «Химия и алгебра» , архивировано 4 февраля 2023 г. в Wayback Machine Nature , 17 : 284. дои : 10.1038/017284a0 . Со страницы 284: «Таким образом, каждый инвариант и ковариант становится выражаемым посредством графика, точно идентичного диаграмме Кекуле или химикографу».

[4] Дж. Дж. Сильвестр (1878 г.) «О применении новой атомной теории к графическому представлению инвариантов и ковариантов бинарных квантов – с тремя приложениями» , Архивировано 2023 г. в 4 февраля Американском журнале математики, чистой и Применено , 1 (1): 64–90. дои : 10.2307/2369436 . JSTOR 2369436 . Термин «график» впервые появляется в этой статье на странице 65.

[3] Гросс, Джонатан Л.; Йеллен, Джей (2004). Справочник по теории графов . ЦРК Пресс . п. 35 . ISBN 978-1-58488-090-5 . Архивировано из оригинала 4 февраля 2023 г. Проверено 16 февраля 2016 г.

[FOOTNOTEBenderWilliamson2010148-4] Бендер и Уильямсон 2010 , с. 148.

[5] См., например, Иянага и Кавада, 69 J , с. 234 или Биггс, с. 4.

[FOOTNOTEBenderWilliamson2010149-6] Бендер и Уильямсон 2010 , с. 149.

[7] Грэм и др., стр. 5.

[FOOTNOTEBenderWilliamson2010161-8] Jump up to: ^а ^б Бендер и Уильямсон 2010 , с. 161.

[9] Стрэнг, Гилберт (2005), Линейная алгебра и ее приложения (4-е изд.), Брукс Коул, ISBN 978-0-03-010567-8

[10] Льюис, Джон (2013), Структуры программного обеспечения Java (4-е изд.), Пирсон, стр. 405, ISBN 978-0133250121

[11] Флетчер, Питер; Хойл, Хьюз; Пэтти, К. Уэйн (1991). Основы дискретной математики (под ред. международного студента). Бостон: Паб PWS-KENT. Компания р. 463. ИСБН 978-0-53492-373-0 . — Взвешенный граф число w ( e ), называемое его весом присвоено это граф, в котором каждому ребру e .

[snatwitter-12] Гранжан, Мартин (2016). «Анализ социальной сети Twitter: составление карты сообщества цифровых гуманитарных наук» . Cogent Искусства и Гуманитарные науки . 3 (1): 1171458. doi : 10.1080/23311983.2016.1171458 . Архивировано из оригинала 02 марта 2021 г. Проверено 16 сентября 2019 г.

[twitterwtf-13] Панкадж Гупта, Ашиш Гоэл, Джимми Лин, Аниш Шарма, Донг Ван и Реза Босаг Заде WTF: Система «за кем следить» в Твиттере. Архивировано 12 июля 2019 г. в Wayback Machine , Материалы 22-й международной конференции по миру. Широкая сеть . дои : 10.1145/2488388.2488433 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]