Метод Нелдера-Мида

Не путать с симплексным алгоритмом Данцига для задачи линейной оптимизации.

Итерация метода Нелдера-Мида в двумерном пространстве.

Поиск по банановой функции Розенброка

Поиск по функции Химмельблау

Поиск минимума Нелдера–Мида функции Симионеску . Вершины симплекса упорядочены по их значению, причем 1 соответствует наименьшему (наилучшему) значению.

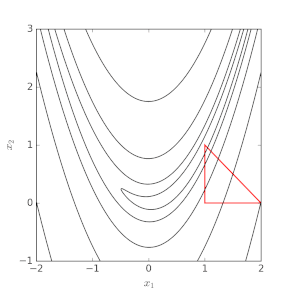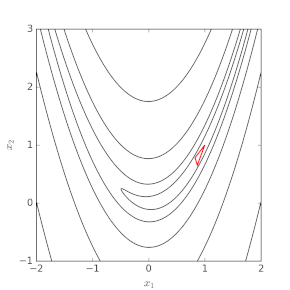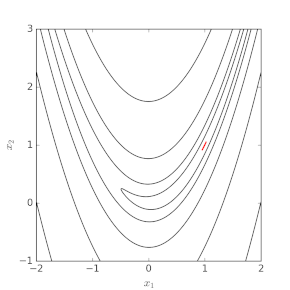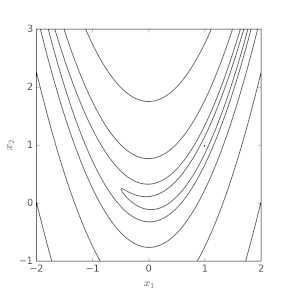
Метод Нелдера-Мида (также метод нисходящего симплекса , метод амебы или метод многогранников ) — численный метод, используемый для поиска минимума или максимума целевой функции в многомерном пространстве. Это метод прямого поиска (основанный на сравнении функций), который часто применяется к задачам нелинейной оптимизации , для которых производные могут быть неизвестны. Однако метод Нелдера-Мида представляет собой эвристический метод поиска, который может сходиться к нестационарным точкам. о проблемах, которые можно решить альтернативными методами.

Методика Нелдера-Мида была предложена Джоном Нелдером и Роджером Мидом в 1965 году. как развитие метода Spendley et al.

Обзор

В методе используется понятие симплекса , который представляет собой особый многогранник из n + 1 вершин в n измерениях. Примеры симплексов включают отрезок прямой в одномерном пространстве, треугольник в двумерном пространстве, тетраэдр в трехмерном пространстве и т. д.

Метод аппроксимирует локальный оптимум задачи с n переменными, когда целевая функция изменяется плавно и унимодальна . Типичные реализации минимизируют функции, а мы максимизируем $f(\mathbf {x} )$ минимизируя $-f(\mathbf {x} )$.

Например, инженер подвесного моста должен выбрать толщину каждой стойки, троса и опоры. Эти элементы взаимозависимы, но нелегко визуализировать влияние изменения любого конкретного элемента. Моделирование таких сложных структур зачастую чрезвычайно затратно в вычислительном отношении и может занимать несколько часов на одно выполнение. Метод Нелдера-Мида в исходном варианте требует не более двух вычислений на итерацию, за исключением операции сжатия , описанной ниже, которая привлекательна по сравнению с некоторыми другими методами оптимизации прямого поиска. Однако общее количество итераций для достижения предложенного оптимума может быть большим.

Нелдер-Мид в n измерениях поддерживает набор из n + 1 контрольных точек, расположенных в виде симплекса . Затем он экстраполирует поведение целевой функции, измеренной в каждой контрольной точке, чтобы найти новую контрольную точку и заменить одну из старых контрольных точек новой, и таким образом метод развивается. Самый простой подход — заменить худшую точку точкой, отраженной через центр тяжести оставшихся n точек. Если эта точка лучше, чем лучшая текущая точка, то мы можем попробовать экспоненциально растянуть эту линию. С другой стороны, если эта новая точка ненамного лучше предыдущей, то мы пересекаем долину и сжимаем симплекс в сторону лучшей точки. Интуитивное объяснение алгоритма из «Численных рецептов»:

Метод нисходящего симплекса теперь состоит из ряда шагов, причем большинство шагов просто перемещают точку симплекса, в которой функция является наибольшей («самая высокая точка»), через противоположную грань симплекса в более низкую точку. Эти шаги называются отражениями, и они созданы для сохранения объема симплекса (и, следовательно, его невырожденности). Когда это возможно, метод расширяет симплекс в том или ином направлении, чтобы сделать более крупные шаги. Когда он достигает «дна долины», метод сжимается в поперечном направлении и пытается сочиться вниз по долине. Если возникает ситуация, когда симплекс пытается «пройти сквозь игольное ушко», он сжимается во всех направлениях, подтягиваясь вокруг своей нижней (лучшей) точки.

В отличие от современных методов оптимизации, эвристика Нелдера-Мида может сходиться к нестационарной точке, если только задача не удовлетворяет более строгим условиям, чем это необходимо для современных методов. Современные усовершенствования эвристики Нелдера – Мида известны с 1979 года.

Существует множество вариаций в зависимости от фактического характера решаемой проблемы. Распространенный вариант использует небольшой симплекс постоянного размера, который примерно следует направлению градиента (что дает самый крутой спуск ). Визуализируйте небольшой треугольник на карте высот, переворачивающийся вниз по долине к местному дну. Этот метод также известен как метод гибкого многогранника . Однако этот метод имеет тенденцию плохо работать по сравнению с методом, описанным в этой статье, поскольку он делает небольшие ненужные шаги в областях, малоинтересных.

Один из возможных вариантов алгоритма НМ.

(Это приблизительно соответствует процедуре, описанной в оригинальной статье Нелдера-Мида.)

Метод Нелдера – Мида в применении к функции Розенброка

Мы пытаемся минимизировать функцию $f(\mathbf {x} )$, где $\mathbf {x} \in \mathbb {R} ^{n}$. Наши текущие контрольные точки: $\mathbf {x} _{1},\ldots ,\mathbf {x} _{n+1}$.

1. Упорядочить по значениям в вершинах:

$f(\mathbf {x} _{1})\leq f(\mathbf {x} _{2})\leq \cdots \leq f(\mathbf {x} _{n+1}).$

Проверьте, должен ли метод остановиться. См. Прекращение (иногда называемое «конвергенцией»).

2. Рассчитать $\mathbf {x} _{o}$, центр тяжести всех точек, кроме $\mathbf {x} _{n+1}$.

3. Размышления

Вычислить отраженную точку $\mathbf {x} _{r}=\mathbf {x} _{o}+\alpha (\mathbf {x} _{o}-\mathbf {x} _{n+1})$ с $\alpha >0$.

Если отраженная точка лучше второй худшей, но не лучше лучшей, т.е. $f(\mathbf {x} _{1})\leq f(\mathbf {x} _{r})<f(\mathbf {x} _{n})$,

затем получим новый симплекс, заменив худшую точку $\mathbf {x} _{n+1}$ с отраженной точкой $\mathbf {x} _{r}$и перейдите к шагу 1.

4. Расширение

Если отраженная точка на данный момент является лучшей точкой, $f(\mathbf {x} _{r})<f(\mathbf {x} _{1})$,

затем вычислите расширенную точку $\mathbf {x} _{e}=\mathbf {x} _{o}+\gamma (\mathbf {x} _{r}-\mathbf {x} _{o})$ с $\gamma >1$.

Если расширенная точка лучше, чем отраженная точка, $f(\mathbf {x} _{e})<f(\mathbf {x} _{r})$,

затем получим новый симплекс, заменив худшую точку $\mathbf {x} _{n+1}$ с расширенной точкой $\mathbf {x} _{e}$ и перейдите к шагу 1;

иначе получим новый симплекс, заменив худшую точку $\mathbf {x} _{n+1}$ с отраженной точкой $\mathbf {x} _{r}$ и перейдите к шагу 1.

5. Сокращение

Вот это точно $f(\mathbf {x} _{r})\geq f(\mathbf {x} _{n})$. (Обратите внимание, что $\mathbf {x} _{n}$ является вторым или «следующим» после худшей точки.)

Если $f(\mathbf {x} _{r})<f(\mathbf {x} _{n+1})$,

затем вычислите сжатую точку снаружи $\mathbf {x} _{c}=\mathbf {x} _{o}+\rho (\mathbf {x} _{r}-\mathbf {x} _{o})$ с $0<\rho \leq 0.5$.

Если стянутая точка лучше, чем отраженная точка, т.е. $f(\mathbf {x} _{c})<f(\mathbf {x} _{r})$,

затем получим новый симплекс, заменив худшую точку $\mathbf {x} _{n+1}$ с контрактной точкой $\mathbf {x} _{c}$ и перейдите к шагу 1;

В противном случае перейдите к шагу 6;

Если $f(\mathbf {x} _{r})\geq f(\mathbf {x} _{n+1})$,

затем вычислите сжатую точку внутри $\mathbf {x} _{c}=\mathbf {x} _{o}+\rho (\mathbf {x} _{n+1}-\mathbf {x} _{o})$ с $0<\rho \leq 0.5$.

Если сжатая точка лучше, чем худшая точка, т.е. $f(\mathbf {x} _{c})<f(\mathbf {x} _{n+1})$,

затем получим новый симплекс, заменив худшую точку $\mathbf {x} _{n+1}$ с контрактной точкой $\mathbf {x} _{c}$ и перейдите к шагу 1;

В противном случае перейдите к шагу 6;

6. Сжать

Заменить все точки кроме лучшей( $\mathbf {x} _{1}$) с

$\mathbf {x} _{i}=\mathbf {x} _{1}+\sigma (\mathbf {x} _{i}-\mathbf {x} _{1})$ и перейдите к шагу 1.

Примечание : $\alpha$, $\gamma$, $\rho$ и $\sigma$ соответственно коэффициенты отражения, расширения, сжатия и сжатия. Стандартные значения $\alpha =1$, $\gamma =2$, $\rho =1/2$ и $\sigma =1/2$.

Для размышления , поскольку $\mathbf {x} _{n+1}$ является вершиной с более высоким связанным значением среди вершин, мы можем ожидать найти более низкое значение при отражении $\mathbf {x} _{n+1}$ в противоположной грани, образованной всеми вершинами $\mathbf {x} _{i}$ кроме $\mathbf {x} _{n+1}$.

Для расширения , если точка отражения $\mathbf {x} _{r}$ — новый минимум вдоль вершин, мы можем ожидать найти интересные значения в направлении от $\mathbf {x} _{o}$ к $\mathbf {x} _{r}$.

Что касается сокращения , если $f(\mathbf {x} _{r})>f(\mathbf {x} _{n})$, мы можем ожидать, что лучшее значение будет внутри симплекса, образованного всеми вершинами $\mathbf {x} _{i}$.

Наконец, сжатие обрабатывает тот редкий случай, когда сокращение от наибольшей точки увеличивает $f$, то, что не может произойти достаточно близко к неособому минимуму. В этом случае мы сжимаемся к самой низкой точке в надежде найти более простой ландшафт. Однако Нэш отмечает, что арифметика конечной точности иногда не может фактически сжать симплекс, и реализовал проверку того, что размер действительно уменьшается.

Начальный симплекс

Начальный симплекс важен. Действительно, слишком маленький начальный симплекс может привести к локальному поиску, следовательно, НМ может легче застрять. Таким образом, этот симплекс должен зависеть от характера проблемы. Однако в исходной статье предлагался симплекс, в котором начальная точка задается как $\mathbf {x} _{1}$, а остальные генерируются с фиксированным шагом по каждому измерению по очереди. Таким образом, метод чувствителен к масштабированию переменных, составляющих $\mathbf {x}$.

Прекращение действия

Критерии необходимы для разрыва итерационного цикла. Нелдер и Мид использовали выборочное стандартное отклонение значений функции текущего симплекса. Если они падают ниже некоторого допуска, то цикл останавливается и самая низкая точка симплекса возвращается в качестве предложенного оптимума. Обратите внимание, что очень «плоская» функция может иметь почти одинаковые значения функции в большой области, поэтому решение будет чувствительно к допуску. Нэш добавляет тест на усадку в качестве еще одного критерия завершения. Обратите внимание, что программы завершаются, а итерации могут сходиться.

См. также

• Оптимизация без производных
• КОБИЛА
• С УОА
• ЛИНКОА
• Нелинейный метод сопряженных градиентов
• Алгоритм Левенберга – Марквардта
• Бройдена-Флетчера-Гольдфарба-Шенно или BFGS. Метод
• Дифференциальная эволюция
• Поиск по шаблону (оптимизация)
• СМА-ES

Дальнейшее чтение

• Авриэль, Мордехай (2003). Нелинейное программирование: анализ и методы . Дуврское издательство. ISBN  978-0-486-43227-4 .
• Куп, ID; Прайс, CJ (2002). «Положительные основы в числовой оптимизации». Вычислительная оптимизация и приложения . 21 (2): 169–176. дои : 10.1023/А:1013760716801 . S2CID   15947440 .
• Гилл, Филип Э.; Мюррей, Уолтер; Райт, Маргарет Х. (1981). «Методы для многомерных негладких функций». Практическая оптимизация . Нью-Йорк: Академическая пресса. стр. 93–96 . ISBN  978-0-12-283950-4 .
• Ковалик, Дж.; Осборн, MR (1968). Методы решения задач безусловной оптимизации . Нью-Йорк: Эльзевир. стр. 24–27 . ISBN  0-444-00041-0 .
• Суонн, штат Вашингтон (1972). «Методы прямого поиска». В Мюррей, В. (ред.). Численные методы неограниченной оптимизации . Нью-Йорк: Академическая пресса. стр. 13–28. ISBN  978-0-12-512250-4 .

Внешние ссылки

• Объяснение и визуализация Нелдера-Мида (Downhill Simplex) с помощью банановой функции Розенброка.
• Джон Буркардт: Код Нелдера-Мида в Matlab . Обратите внимание, что вариант метода Нелдера-Мида также реализуется функцией Matlab fminsearch.
• Оптимизация Нелдера-Мида в Python в библиотеке SciPy.
• nelder-mead — реализация метода Нелдера-Мида на Python.
• NelderMead() — реализация Go/Golang.
• SOVA 1.0 (бесплатное ПО) — симплексная оптимизация для различных приложений
• [1] - HillStormer, практический инструмент для нелинейной, многомерной и линейной симплексной оптимизации с ограничениями от Нелдера Мида.