Радикальная ось

Эта статья о радикальной оси, используемой в геометрии. Чтобы узнать о анимационной студии, см. Radical Axis (студия) .

  Два круга с центрами M ₁ , M ₂

  Радикальная ось, с точкой отбора P

  Касательные расстояния от обеих окружностей до P

Касательные линии должны быть одинаковой длины для любой точки радикальной оси: $|PT_{1}|=|PT_{2}|.$ Если P , T ₁ , T ₂ лежат на общей касательной, P — середина ⁠ то ${\overline {T_{1}T_{2}}}.$⁠

В евклидовой геометрии радикальная ось двух неконцентрических окружностей — это набор точек, степени которых по отношению к окружностям равны. По этой причине радикальную ось также называют линией власти или биссектрисой двух кругов. Подробно:

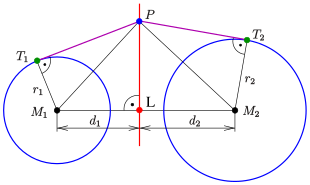
Для двух окружностей c ₁ , c ₂ с центрами M ₁ , M ₂ и радиусами r ₁ , r ₂ степени точки P относительно окружностей равны

$\Pi _{1}(P)=|PM_{1}|^{2}-r_{1}^{2},\qquad \Pi _{2}(P)=|PM_{2}|^{2}-r_{2}^{2}.$

Точка P принадлежит радикальной оси, если

$\Pi _{1}(P)=\Pi _{2}(P).$

Если окружности имеют две общие точки, радикальная ось является общей секущей окружностей.
Если точка P находится за пределами окружностей, точка P имеет одинаковое касательное расстояние до обеих окружностей.
Если радиусы равны, радикальной осью является отрезка биссектриса M ₁ , M ₂ .
В любом случае радикальная ось — это линия, перпендикулярная ${\overline {M_{1}M_{2}}}.$

Об обозначениях

Обозначение радикальная ось использовалось французским математиком М. Шаслем как радикал-топор .
JV Poncelet использовал Chorde Ideale .
Й. Плюкер ввел термин Хордейл .
Й. Штайнер назвал радикальной осью линию равных сил ( нем . Linie der Gleichen Potenz ), которая вела к линии власти ( Power line ).

Характеристики

Геометрическая форма и ее положение.

Позволять ${\vec {x}},{\vec {m}}_{1},{\vec {m}}_{2}$ быть векторами положения точек $P,M_{1},M_{2}$. Тогда определяющее уравнение радикальной линии можно записать в виде:

$({\vec {x}}-{\vec {m}}_{1})^{2}-r_{1}^{2}=({\vec {x}}-{\vec {m}}_{2})^{2}-r_{2}^{2}\quad \leftrightarrow \quad 2{\vec {x}}\cdot ({\vec {m}}_{2}-{\vec {m}}_{1})+{\vec {m}}_{1}^{2}-{\vec {m}}_{2}^{2}+r_{2}^{2}-r_{1}^{2}=0$

Определение и расчет $d_{1},d_{2}$

Из правильного уравнения получаем

• Набор точек радикальной оси действительно является линией и перпендикулярен линии, проходящей через центры окружностей.

( ${\vec {m}}_{2}-{\vec {m}}_{1}$ является вектором нормали к радикальной оси!)

Разделив уравнение на $2|{\vec {m}}_{2}-{\vec {m}}_{1}|$, получается гессенская нормальная форма . Подстановка векторов положения центров дает расстояния центров до радикальной оси:

$d_{1}={\frac {d^{2}+{r_{1}}^{2}-{r_{2}}^{2}}{2d}}\ ,\qquad d_{2}={\frac {d^{2}+{r_{2}}^{2}-{r_{1}}^{2}}{2d}}$,

с $d=|M_{1}M_{2}|$.

( $d_{i}$ может быть отрицательным, если $L$ не между $M_{1},M_{2}$.)

Если окружности пересекаются в двух точках, радикальная линия проходит через общие точки. Если они касаются только друг друга, радикальная линия является общей касательной.

Особые позиции

Радикальная ось: варианты

• Радикальная ось двух пересекающихся окружностей является их общей секущей линией.

Радикальная ось двух соприкасающихся окружностей является их общей касательной.

Радикальная ось двух непересекающихся кругов является общей секущей двух удобных равносильных кругов (см. ниже).

Ортогональные круги

Точки касания касательных через $P$ лежат на ортогональном круге (зеленом)

• Для точки $P$ вне круга $c_{i}$ и две точки касания $S_{i},T_{i}$ уравнение $|PS_{i}|^{2}=|PT_{i}|^{2}=\Pi _{i}(P)$ держит и $S_{i},T_{i}$ лежать на круге $c_{o}$ с центром $P$ и радиус ${\sqrt {\Pi _{i}(P)}}$. Круг $c_{o}$ пересекает $c_{i}$ ортогональный. Следовательно:

Если $P$ является точкой радикальной оси, то четыре точки $S_{1},T_{1},S_{2},T_{2}$ лежать на круге $c_{o}$, который пересекает данные окружности $c_{1},c_{2}$ ортогонально .

• Радикальная ось состоит из всех центров окружностей , которые пересекают данные окружности ортогонально.

Система ортогональных окружностей

Описанный в предыдущем разделе метод построения пучка окружностей, пересекающих две заданные окружности ортогонально, можно распространить на построение двух ортогонально пересекающихся систем окружностей:

Позволять $c_{1},c_{2}$ быть двумя отдельно лежащими кругами (как в предыдущем разделе), $M_{1},M_{2},r_{1},r_{2}$ их центры и радиусы и $g_{12}$ их радикальная ось. Теперь все круги будут определяться с центрами на линии. ${\overline {M_{1}M_{2}}}$, которые вместе с $c_{1}$ линия $g_{12}$ как радикальная ось. Если $\gamma _{2}$ это такой круг, центр которого имеет расстояние $\delta$ в центр $M_{1}$ и радиус $\rho _{2}$. Из результата предыдущего раздела получаем уравнение

$d_{1}={\frac {\delta ^{2}+r_{1}^{2}-\rho _{2}^{2}}{2\delta }}\quad$, где $d_{1}>r_{1}$ фиксированы.

С $\delta _{2}=\delta -d_{1}$ уравнение можно переписать так:

$\delta _{2}^{2}=d_{1}^{2}-r_{1}^{2}+\rho _{2}^{2}$.

Система ортогональных окружностей: построение

Если радиус $\rho _{2}$ задано, из этого уравнения находится расстояние $\delta _{2}$ к (фиксированной) радикальной оси нового центра. На схеме цвет новых кружков фиолетовый. Любой зеленый круг (см. схему) имеет центр на радикальной оси и пересекает круги. $c_{1},c_{2}$ ортогонально и, следовательно, все новые круги (фиолетовые) тоже. Выбор (красной) радикальной оси в качестве оси Y и линии ${\overline {M_{1}M_{2}}}$ в качестве оси X два пучка окружностей имеют уравнения:

фиолетовый: $\ \ \ (x-\delta _{2})^{2}+y^{2}=\delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}$

зеленый: $\ x^{2}+(y-y_{g})^{2}=y_{g}^{2}+d_{1}^{2}-r_{1}^{2}\ .$

( $\;(0,y_{g})$ находится в центре зеленого круга.)

Характеристики:
а) Любые два зеленых круга пересекаются на оси х в точках $P_{1/2}={\big (}\pm {\sqrt {d_{1}^{2}-r_{1}^{2}}},0{\big )}$, полюса ортогональной системы окружностей. Это означает, что ось X — это радикальная линия зеленых кругов.
б) Фиолетовые круги не имеют общих точек. Но если рассматривать действительную плоскость как часть комплексной плоскости, то любые два фиолетовых круга пересекаются по оси y (их общей радикальной оси) в точках $Q_{1/2}={\big (}0,\pm i{\sqrt {d_{1}^{2}-r_{1}^{2}}}{\big )}$.

Параболическая ортогональная система

Коаксиальные круги: виды

Особые случаи:
а) В случае $d_{1}=r_{1}$ зеленые круги соприкасаются друг с другом в начале координат, при этом ось X является общей касательной, а фиолетовые круги имеют ось Y как общую касательную. Такая система окружностей называется коаксиальными параболическими окружностями (см. ниже).
б) Сокращение $c_{1}$ в его центр $M_{1}$, я. И. $r_{1}=0$, уравнения принимают более простой вид и получают $M_{1}=P_{1}$.

Заключение:
а) Для любого реального $w$ карандаш кругов

$\;c(\xi ):\;(x-\xi )^{2}+y^{2}-\xi ^{2}-w=0\ :$

обладает свойством: ось Y является осью радикальной $c(\xi _{1}),c(\xi _{2})$.

В случае $w>0$ круги $c(\xi _{1}),c(\xi _{2})$ пересекаться в точках $P_{1/2}=(0,\pm {\sqrt {w}})$.

В случае $w<0$ у них нет общих точек соприкосновения.

В случае $w=0$ они касаются $(0,0)$ а ось Y — их общая касательная.

б) Для любого реального $w$ два карандаша с кругами

$c_{1}(\xi ):\;(x-\xi )^{2}+y^{2}-\xi ^{2}-w=0\ ,$

$c_{2}(\eta ):\;x^{2}+(y-\eta )^{2}-\eta ^{2}+w=0\$

образуют систему ортогональных окружностей . Это означает: любые два круга $c_{1}(\xi ),c_{2}(\eta )$ пересекаются ортогонально.

в) Из уравнений пункта б) получается бескоординатное представление:

Ортогональная система окружностей данным полюсам $P_{1},P_{2}$

По заданным пунктам $P_{1},P_{2}$, их середина $O$ и их биссектриса отрезка $g_{12}$ два уравнения

$|XM|^{2}=|OM|^{2}-|OP_{1}|^{2}\ ,$

$|XN|^{2}=|ON|^{2}+|OP_{1}|^{2}=|NP_{1}|^{2}$

с $M$ на ${\overline {P_{1}P_{2}}}$, но не между $P_{1},P_{2}$, и $N$ на $g_{12}$

описывают ортогональную систему окружностей, однозначно определяемую $P_{1},P_{2}$ которые являются полюсами системы.

Для $P_{1}=P_{2}=O$ нужно прописать оси $a_{1},a_{2}$ системы тоже. Система является параболической :

$|XM|^{2}=|OM|^{2}\ ,\quad |XN|^{2}=|ON|^{2}$

с $M$ на $a_{1}$ и $N$ на $a_{2}$.

Конструкция линейки и циркуля:

Ортогональная система окружностей: построение линейки и циркуля

Система ортогональных окружностей однозначно определяется своими полюсами $P_{1},P_{2}$:

1. Оси (радикальные оси) — это линии ${\overline {P_{1}P_{2}}}$ и биссектриса отрезка $g_{12}$ полюсов.
2. Кружочки (зеленые на схеме) через $P_{1},P_{2}$ иметь свои центры на $g_{12}$. Их можно легко нарисовать. Для точки $N$ радиус $\;r_{N}=|NP_{1}|\;$.
3. Чтобы вторым карандашом (на схеме синий) нарисовать круг с центром $M$ на ${\overline {P_{1}P_{2}}}$, определяется радиус $r_{M}$ применяя теорему Пифагора : $\;r_{M}^{2}=|OM|^{2}-|OP_{1}|^{2}\;$ (см. схему).

В случае $P_{1}=P_{2}$ оси необходимо выбирать дополнительно. Система параболическая и ее легко нарисовать.

Коаксиальные круги

Определение и свойства:

Позволять $c_{1},c_{2}$ быть двумя кругами и $\Pi _{1},\Pi _{2}$ их силовые функции. Тогда для любого $\lambda \neq 1$

• $\Pi _{1}(x,y)-\lambda \Pi _{2}(x,y)=0$

это уравнение окружности $c(\lambda )$ (см. ниже). Такая система окружностей называется коаксиальными окружностями, порожденными окружностями $c_{1},c_{2}$.(В случае $\lambda =1$ уравнение описывает радикальную ось $c_{1},c_{2}$.)

Степенная функция $c(\lambda )$ является

$\ \Pi (\lambda ,x,y)={\frac {\Pi _{1}(x,y)-\lambda \Pi _{2}(x,y)}{1-\lambda }}$.

Нормированное уравнение ( коэффициенты $x^{2},y^{2}$ являются $1$) из $c(\lambda )$ является $\ \Pi (\lambda ,x,y)=0$.

Простой расчет показывает:

• $c(\lambda ),c(\mu ),\ \lambda \neq \mu \ ,$ имеют ту же радикальную ось, что и $c_{1},c_{2}$.

Разрешение $\lambda$ двигаться в бесконечность, человек признает, что $c_{1},c_{2}$ являются членами системы коаксиальных кругов: $c_{1}=c(0),\;c_{2}=c(\infty )$.

(Э): Если $c_{1},c_{2}$ пересекаться в двух точках $P_{1},P_{2}$, любой круг $c(\lambda )$ содержит $P_{1},P_{2}$тоже и линия ${\overline {P_{1}P_{2}}}$ является их общей радикальной осью. Такая система называется эллиптической .
(П): Если $c_{1},c_{2}$ касаются ​ ​ $P$, любая окружность касается $c_{1},c_{2}$ в точку $P$, слишком. Общая касательная — это их общая радикальная ось. Такая система называется параболической .
(H): Если $c_{1},c_{2}$ не имеют общих точек , то любая пара системы тоже. Радикальная ось любой пары окружностей является радикальной осью $c_{1},c_{2}$. Система называется гиперболической .

Подробно:

Вводя координаты такие, что

$c_{1}:(x-d_{1})^{2}+y^{2}=r_{1}^{2}$

$c_{2}:(x-d_{2})^{2}+y^{2}=d_{2}^{2}+r_{1}^{2}-d_{1}^{2}$,

тогда ось Y является их радикальной осью (см. выше).

Вычисление степенной функции $\Pi (\lambda ,x,y)$ дает нормированное уравнение окружности:

$c(\lambda ):\ x^{2}+y^{2}-2{\tfrac {d_{1}-\lambda d_{2}}{1-\lambda }}\;x+d_{1}^{2}-r_{1}^{2}=0\ .$

Завершение поля и замена $\delta _{2}={\tfrac {d_{1}-\lambda d_{2}}{1-\lambda }}$ (координата x центра) дает центрированную форму уравнения

$c(\lambda ):\ (x-\delta _{2})^{2}+y^{2}=\delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}$.

В случае $r_{1}>d_{1}$ круги $c_{1},c_{2},c(\lambda )$ есть две точки

$P_{1}={\big (}0,{\sqrt {r_{1}^{2}-d_{1}^{2}}}{\big )},\quad P_{2}={\big (}0,-{\sqrt {r_{1}^{2}-d_{1}^{2}}}{\big )}$

в общем и целом система коаксиальных окружностей эллиптическая .

В случае $r_{1}=d_{1}$ круги $c_{1},c_{2},c(\lambda )$ иметь точку $P_{0}=(0,0)$ в общем и система является параболической .

В случае $r_{1}<d_{1}$ круги $c_{1},c_{2},c(\lambda )$ не имеют общих точек и система является гиперболической .

Альтернативные уравнения:
1) В определяющем уравнении коаксиальной системы окружностей можно использовать и кратные степенным функциям.
2) Уравнение одной из окружностей можно заменить уравнением искомой радикальной оси. Радикальную ось можно рассматривать как круг бесконечно большого радиуса. Например:

$(x-x_{1})^{2}+y^{2}-r_{1}^{2}\ -\ \lambda \;2(x-x_{2})\ =0\ \Leftrightarrow$

$(x-(x_{1}+\lambda ))^{2}+y^{2}=(x_{1}+\lambda )^{2}+r_{1}^{2}-x_{1}^{2}-2\lambda x_{2}$,

описывает все круги, у которых с первым кругом проходит линия $x=x_{2}$ как радикальная ось.
3) Для выражения равного статуса двух кругов часто используется следующая форма:

$\mu \Pi _{1}(x,y)+\nu \Pi _{2}(x,y)=0\;.$

Но в этом случае представление окружности параметрами $\mu ,\nu$ не является уникальным .

Приложения:
а) Инверсии окружностей и преобразования Мёбиуса сохраняют углы и обобщенные окружности . Следовательно, ортогональные системы окружностей играют существенную роль в исследованиях этих отображений.
б) В электромагнетизме коаксиальные круги выглядят как силовые линии .

Радикальный центр трех кругов, построение радикальной оси

Радикальный центр трех кругов
Зеленый круг пересекает три круга ортогонально.

• На три круга $c_{1},c_{2},c_{3}$, никакие две из которых не концентричны, имеется три радикальные оси $g_{12},g_{23},g_{31}$. Если центры окружностей не лежат на одной прямой, радикальные оси пересекаются в одной точке. $R$, радикальный центр трех кругов. Ортогональный круг с центром вокруг $R$ двух кругов также ортогонален третьему кругу ( радикальный круг ).

Доказательство: радикальная ось $g_{ik}$ содержит все точки, имеющие одинаковое касательное расстояние к окружностям $c_{i},c_{k}$. Точка пересечения $R$ из $g_{12}$ и $g_{23}$ имеет одинаковое касательное расстояние ко всем трем окружностям. Следовательно $R$ является точкой радикальной оси $g_{31}$, слишком.

Это свойство позволяет построить радикальную ось двух непересекающихся окружностей. $c_{1},c_{2}$ с центрами $M_{1},M_{2}$: Нарисуйте третий круг. $c_{3}$ с центром, не коллинеарным данным центрам, который пересекается $c_{1},c_{2}$. Радикальные оси $g_{13},g_{23}$ можно нарисовать. Точкой их пересечения является радикальный центр $R$ из трех кругов и лежит на $g_{12}$. Линия через $R$ который перпендикулярен ${\overline {M_{1}M_{2}}}$ радикальная ось $g_{12}$.

Дополнительный метод строительства:

Построение радикальной оси окружностями $c'_{1},c'_{2}$ равной силы. Это $\Pi _{1}(P_{1})=\Pi _{2}(P_{2})$.

Все точки, имеющие одинаковую мощность по отношению к данному кругу $c$ лежать на окружности, концентрической $c$. Назовем это кругом эквимощности . Это свойство можно использовать для дополнительного способа построения радикальной оси двух окружностей:

Для двух непересекающихся окружностей $c_{1},c_{2}$, можно нарисовать два равносильных круга $c'_{1},c'_{2}$, которые имеют одинаковую мощность по отношению к $c_{1},c_{2}$ (см. схему). Подробно: $\Pi _{1}(P_{1})=\Pi _{2}(P_{2})$. Если мощность достаточно велика, круги $c'_{1},c'_{2}$ имеют две общие точки, лежащие на радикальной оси $g_{12}$.

Связь с биполярными координатами

В общем, любые две непересекающиеся, неконцентрические окружности можно сопоставить с окружностями системы биполярных координат . В этом случае радикальная ось — это просто $y$-ось этой системы координат. Каждый круг на оси, проходящий через два фокуса системы координат, пересекает два круга ортогонально. Максимальный набор окружностей, все из которых имеют центры на данной прямой и все пары имеют одну и ту же радикальную ось, известен как пучок коаксиальных окружностей .

Радикальный центр в трилинейных координатах

Если окружности представить в трехлинейных координатах обычным способом, то в качестве некоторого определителя удобно указать их радикальный центр. В частности, пусть X = x : y : z обозначает переменную точку в плоскости треугольника ABC с длинами сторон a = | до нашей эры |, б = | СА |, с = | AB |, и представим круги следующим образом:

( dx + ey + fz )( ax + by + cz ) + g ( ayz + bzx + cxy ) = 0

( hx + iy + jz )( ax + by + cz ) + k ( ayz + bzx + cxy ) = 0

( lx + my + nz )( ax + by + cz ) + p ( ayz + bzx + cxy ) = 0

Тогда радикальный центр – это точка

$\det {\begin{bmatrix}g&k&p\\e&i&m\\f&j&n\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\f&j&n\\d&h&l\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\d&h&l\\e&i&m\end{bmatrix}}.$

Радикальная плоскость и гиперплоскость

Радикальная плоскость двух неконцентрических сфер в трех измерениях определяется аналогично: это место точек, из которых касательные к двум сферам имеют одинаковую длину. Тот факт, что этот локус представляет собой плоскость, следует из вращения в третьем измерении из того факта, что радикальная ось представляет собой прямую линию.

То же определение можно применить к гиперсферам в евклидовом пространстве любой размерности, давая радикальную гиперплоскость двух неконцентрических гиперсфер.

Ссылки

• Р. А. Джонсон (1960). Продвинутая евклидова геометрия: элементарный трактат о геометрии треугольника и круга (перепечатка издания 1929 года под ред. Хоутона Миффлина). Нью-Йорк: Dover Publications. стр. 31–43 . ISBN  978-0-486-46237-0 .

Дальнейшее чтение

• К. Стэнли Огилви (1990). Экскурсии по геометрии . Дувр. стр. 17–23 . ISBN  0-486-26530-7 .
• HSM Coxeter , SL Greitzer (1967). Возвращение к геометрии . Вашингтон, округ Колумбия : Математическая ассоциация Америки . стр. 31–36 , 160–161. ISBN  978-0-88385-619-2 .
• Кларк Кимберлинг, «Центры треугольников и центральные треугольники», Congressus Numerantium 129 (1998) i – xxv, 1–295.

Внешние ссылки

• Вайсштейн, Эрик В. «Радикальная линия» . Математический мир .
• Вайсштейн, Эрик В. «Хордальная теорема» . Математический мир .
• Анимация в Cut-the-knot