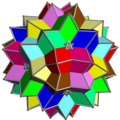
Соединение десяти октаэдров

Соединения десяти октаэдров
Тип	Однородный состав
Индекс	УК 15 и УК 16
Многогранники	10 октаэдров
Лица	20+60 треугольников
Края	120
Вершины	60
Группа симметрии	икосаэдрический ( I h )
Подгруппа, ограничивающаяся одним компонентом	3-кратный антипризматический ( D 3d )

3D модель соединения десяти октаэдров UC ₁₅

3D модель соединения десяти октаэдров UC ₁₆

Соединения десяти октаэдров UC ₁₅ и UC ₁₆ представляют собой два однородных многогранных соединения . Они состоят из симметричного расположения 10 октаэдров , рассматриваемых как треугольные антипризмы , выровненных по осям тройной вращательной симметрии икосаэдра . Эти два соединения различаются ориентацией своих октаэдров: каждое соединение можно превратить в другое, повернув каждый октаэдр на 60 градусов.

Декартовы координаты

Декартовы координаты вершин этого соединения — это все циклические перестановки

(0, ±(t ⁻¹ √ 2 + 2 s τ), ±(τ √ 2 − 2sτ ⁻¹ ))

(±( √ 2 − s τ ² ), ±( √ 2 + s (2τ − 1)), ±( √ 2 + s τ ⁻² ))

(±(т ⁻¹ √ 2 − s τ), ±(τ √ 2 + s τ ⁻¹ ), ±3 s )

где τ = (1 + √ 5 )/2 — золотое сечение (иногда обозначаемое φ), а s равно +1 или −1. Установка s = −1 дает UC ₁₅ , а s = +1 дает UC ₁₆ .

См. также

• Соединение трех октаэдров
• Соединение четырех октаэдров
• Соединение пяти октаэдров
• Соединение двадцати октаэдров

Ссылки

• Скиллинг, Джон (1976), «Однородные соединения однородных многогранников», Mathematical Proceedings of the Cambridge Philosophical Society , 79 : 447–457, doi : 10.1017/S0305004100052440 , MR   0397554 .