Анализ баланса потоков

Анализ баланса потоков ( FBA в масштабе генома ) — математический метод моделирования метаболизма при реконструкциях метаболических сетей . По сравнению с традиционными методами моделирования FBA менее трудоемкий с точки зрения входных данных, необходимых для построения модели. Моделирование, выполняемое с использованием FBA, не требует больших вычислительных затрат и позволяет рассчитать стационарные метаболические потоки для больших моделей (более 2000 реакций) за несколько секунд на современных персональных компьютерах. Соответствующий метод анализа метаболических путей направлен на поиск и составление списка всех возможных путей между метаболитами.

Результаты ФБА на подготовленной метаболической сети шести основных реакций гликолиза . Прогнозируемый поток через каждую реакцию пропорционален ширине линии. Целевая функция выделена красным, ограничения на импорт альфа-D-глюкозы и бета-D-глюкозы представлены красными столбцами.

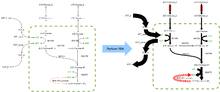
FBA находит применение в биотехнологии для систематического выявления модификаций метаболических сетей микробов, используемых в процессах ферментации, которые повышают выход продуктов промышленно важных химических веществ, таких как этанол и янтарная кислота. Его также использовали для идентификации предполагаемых мишеней лекарств при раке. и патогены, рациональный дизайн культурных сред, и взаимодействия хозяин-патоген . Результаты FBA можно визуализировать с помощью карт потоков, аналогичных изображению справа, которое иллюстрирует стационарные потоки, переносимые реакциями гликолиза . Толщина стрелок пропорциональна потоку через реакцию.

FBA формализует систему уравнений, описывающую изменения концентрации в метаболической сети, как скалярное произведение матрицы стехиометрических коэффициентов (стехиометрическая матрица S ) и вектора v нерешенных потоков. Правая часть скалярного произведения представляет собой вектор нулей, представляющий систему в устойчивом состоянии . Затем линейное программирование используется для расчета решения потоков, соответствующих установившемуся состоянию.

История

Некоторые из самых ранних работ в FBA относятся к началу 1980-х годов. Папуцакис продемонстрировал, что можно построить уравнения баланса потоков, используя метаболическую карту. Это был Ватсон, однако он первым представил идею использования линейного программирования и целевой функции для определения потоков на пути. Первое значительное исследование было впоследствии опубликовано Феллом и Смоллом. который использовал анализ баланса потоков вместе с более сложными целевыми функциями для изучения ограничений синтеза жира.

Симуляторы

Пример нелетальной делеции гена в образце метаболической сети с потоками, показанными по весу реакционных линий, рассчитанным с помощью FBA. Здесь поток через целевую функцию уменьшается вдвое, но все еще присутствует.

Пример делеции летального гена в образце метаболической сети с потоками, показанными по весу реакционных линий, рассчитанным с помощью FBA. Здесь нет потока через целевую функцию, что моделирует, что путь больше не функционирует.

Ингибирование реакции: график прогнозируемой FBA скорости роста (ось y) в зависимости от уменьшения притока кислорода (ось x) в модели E.coli FBA.

Трехмерная фенотипическая фазовая плоскость, демонстрирующая влияние различных входных потоков глюкозы и глицерина на скорость роста микобактерий туберкулеза. Ось X представляет приток глицерина, а ось Y представляет приток глюкозы, высота поверхности (красная) представляет значение потока роста для каждой комбинации входных потоков.

Версия уровня фенотипической фазовой плоскости, показывающая влияние различных входных потоков глюкозы и глицерина на скорость роста Mycobacterium Tuberculosis. Ось X представляет приток глицерина, а ось Y представляет приток глюкозы, цвет представляет величину притока роста.

Сравнение графиков корреляции летальных парных делеций в разных подсистемах для E.coli (слева) и M.tuberculosis (справа).

FBA не требует больших вычислительных затрат: расчет оптимальных потоков для производства биомассы для типичной сети занимает порядка секунд (около 2000 реакций). Это означает, что эффект удаления реакций из сети и/или изменения ограничений потока можно разумно смоделировать на одном компьютере.

Исследования делеции генов/реакций и возмущений

Удаление одной реакции

Часто используемый метод поиска в метаболической сети реакций, которые особенно важны для производства биомассы. Поочередно удаляя каждую реакцию в сети и измеряя прогнозируемый поток через функцию биомассы, каждую реакцию можно классифицировать как существенную (если поток через функцию биомассы существенно снижается) или несущественную (если поток через функцию биомассы существенно снижается). функция не изменена или лишь незначительно снижена).

Удаление парной реакции

Удаление парных реакций всех возможных пар реакций полезно при поиске мишеней для лекарств, поскольку позволяет моделировать многоцелевые методы лечения либо одним препаратом с несколькими мишенями, либо комбинациями лекарств. Исследования двойной делеции также могут количественно оценить синтетические летальные взаимодействия между различными путями, обеспечивая меру вклада пути в общую надежность сети.

Одиночные и множественные делеции генов

Гены связаны с реакциями, катализируемыми ферментами, с помощью логических выражений , известных как выражения «ген-белок-реакция» (GPR). Обычно GPR принимает форму (ген A И ген B), чтобы указать, что продукты генов A и B представляют собой белковые субъединицы, которые собираются в полноценный белок, и, следовательно, отсутствие любого из них приведет к удалению реакции. С другой стороны, если GPR представляет собой (ген A ИЛИ ген B), это означает, что продукты генов A и B являются изоферментами . Следовательно, можно оценить эффект делеции одного или нескольких генов путем оценки GPR как логического выражения. Если GPR оценивается как false , реакция ограничивается нулем в модели до выполнения FBA. Таким образом, нокаут генов можно моделировать с помощью FBA.

Интерпретация результатов делеции гена и реакции

Полезность анализа ингибирования реакций и делеций становится наиболее очевидной, если для сети, изучаемой с помощью FBA, собрана матрица ген-белковых реакций. Матрица ген-белковых реакций представляет собой бинарную матрицу, соединяющую гены с созданными из них белками. Используя эту матрицу, существенность реакции можно преобразовать в существенность гена, указывая дефекты генов, которые могут вызывать определенный фенотип заболевания, или необходимые белки/ферменты (и, следовательно, какие ферменты являются наиболее перспективными мишенями для лекарств в патогенах). Однако матрица ген-белок-реакция не определяет булеву связь между генами по отношению к ферменту, а просто указывает на связь между ними. Поэтому его следует использовать только в том случае, если логическое выражение GPR недоступно.

Ингибирование реакции

Эффект ингибирования реакции, а не полного ее устранения, можно смоделировать в FBA, ограничив разрешенный поток через нее. Эффект ингибирования можно классифицировать как летальный или нелетальный, применяя те же критерии, что и в случае делеции, где используется подходящий порог, чтобы отличить «значительно сниженный» от «незначительно сниженного». Обычно выбор порога является произвольным, но разумную оценку можно получить из экспериментов по росту, в которых фактически выполняются моделируемые ингибирования/делеции и измеряется скорость роста.

Оптимизация среды роста

Чтобы разработать оптимальную среду для роста с точки зрения повышенной скорости роста или секреции полезных побочных продуктов, можно использовать метод, известный как анализ фенотипической фазовой плоскости. PhPP предполагает многократное применение FBA к модели при одновременном изменении ограничений на поглощение питательных веществ и наблюдении значения целевой функции (или потоков побочных продуктов). PhPP позволяет найти оптимальную комбинацию питательных веществ, которая благоприятствует определенному фенотипу или режиму метаболизма, что приводит к более высоким темпам роста или секреции промышленно полезных побочных продуктов. Было показано, что прогнозируемые темпы роста бактерий в различных средах хорошо коррелируют с экспериментальными результатами. а также определить точную минимальную среду для культуры Salmonella typhimurium .

Взаимодействие хозяина и патогена

Микробиота человека представляет собой сложную систему, насчитывающую до 400 триллионов микробов и бактерий, взаимодействующих друг с другом и с хозяином. Понять ключевые факторы в этой системе; предлагается многомасштабный динамический анализ баланса потоков, поскольку FBA классифицируется как менее трудоемкий.

Математическое описание

В отличие от традиционно используемого подхода метаболического моделирования с использованием связанных обыкновенных дифференциальных уравнений , анализ баланса потоков требует очень мало информации с точки зрения кинетических параметров фермента и концентрации метаболитов в системе. Это достигается за счет двух допущений: устойчивого состояния и оптимальности. Первое предположение состоит в том, что смоделированная система вошла в устойчивое состояние, в котором концентрации метаболитов больше не меняются, т.е. в каждом метаболитном узле потоки производства и потребления компенсируют друг друга. Второе предположение заключается в том, что в ходе эволюции организм был оптимизирован для достижения какой-то биологической цели, например оптимального роста или сохранения ресурсов. Допущение об устойчивом состоянии сводит систему к набору линейных уравнений, которые затем решаются, чтобы найти распределение потока, которое удовлетворяет условию установившегося состояния с учетом ограничений стехиометрии, при этом максимизируя значение псевдореакции (целевая функция). представляющий собой преобразование предшественников биомассы в биомассу.

Предположение об устойчивом состоянии восходит к идеям материального баланса, разработанным для моделирования роста микробных клеток в ферментерах в биотехнологии. Во время роста микроорганизмов для образования биомассы расходуется субстрат, состоящий из сложной смеси источников углерода, водорода, кислорода и азота, а также микроэлементов.Модель материального баланса для этого процесса выглядит следующим образом:

$\mathrm {Input} =\mathrm {Output} +\mathrm {Accumulation}$

Если мы считаем, что система микробных клеток находится в устойчивом состоянии, то мы можем обнулить член накопления и свести уравнения материального баланса к простым алгебраическим уравнениям. В такой системе субстрат становится входом в систему, который потребляется, а производимая биомасса становится выходом системы. Тогда материальный баланс можно представить как:

$\mathrm {Input} =\mathrm {Output}$

$\mathrm {Input} -\mathrm {Output} =\mathrm {0}$

Математически алгебраические уравнения можно представить как скалярное произведение матрицы коэффициентов и вектора неизвестных. Поскольку предположение об устойчивом состоянии сводит член накопления к нулю. Система может быть записана как:

$\qquad A\cdot \mathbf {x} =\mathbf {0}$

Распространив эту идею на метаболические сети, можно представить метаболическую сеть как стехиометрически сбалансированную систему уравнений. Переходя к матричному формализму, мы можем представить уравнения как скалярное произведение матрицы коэффициентов стехиометрии (стехиометрическая матрица $S$) и вектор потоков $\mathbf {v}$ в качестве неизвестных и установите правую часть на 0, подразумевая устойчивое состояние.

$\qquad S\cdot \mathbf {v} =\mathbf {0}$

Метаболические сети обычно имеют больше реакций, чем метаболиты, и это дает недоопределенную систему линейных уравнений, содержащую больше переменных, чем уравнений. Стандартным подходом к решению таких недоопределенных систем является применение линейного программирования .

Линейные программы — это задачи, которые можно выразить в канонической форме :

${\begin{aligned}&{\text{maximize}}&&\mathbf {c} ^{\mathrm {T} }\mathbf {x} \\&{\text{subject to}}&&A\mathbf {x} \leq \mathbf {b} \\&{\text{and}}&&\mathbf {x} \geq \mathbf {0} \end{aligned}}$

где x представляет собой вектор переменных (подлежащих определению), c и b представляют собой векторы (известных) коэффициентов, A представляет собой (известную) матрицу коэффициентов, и $(\cdot )^{\mathrm {T} }$ это транспонирование матрицы . Выражение, которое необходимо максимизировать или минимизировать, называется целевой функцией ( c ^Т х в данном случае). Неравенства A x ≤ b представляют собой ограничения, определяющие выпуклый многогранник , по которому должна быть оптимизирована целевая функция.

Линейное программирование требует определения целевой функции. Оптимальным решением задачи ЛП считается такое решение, которое максимизирует или минимизирует значение целевой функции в зависимости от конкретного случая. В случае анализа баланса потоков целевая функция Z для LP часто определяется как производство биомассы. Производство биомассы моделируется с помощью уравнения, представляющего сосредоточенную реакцию, которая преобразует различные предшественники биомассы в одну единицу биомассы.

Следовательно, каноническая форма задачи анализа баланса потоков будет такой:

${\begin{aligned}&{\text{maximize}}&&\mathbf {c} ^{\mathrm {T} }\mathbf {v} \\&{\text{subject to}}&&S\mathbf {v} =\mathbf {0} \\&{\text{and}}&&\mathbf {lowerbound} \leq \mathbf {v} \leq \mathbf {upperbound} \end{aligned}}$

где $\mathbf {v}$ представляет собой вектор потоков (подлежит определению), $S$ (известная) матрица коэффициентов. Выражение, которое необходимо максимизировать или минимизировать, называется целевой функцией ( $\mathbf {c} ^{\mathrm {T} }\mathbf {v}$ в этом случае). Неравенства $\mathbf {lowerbound} \leq \mathbf {v}$ и $\mathbf {v} \leq \mathbf {upperbound}$ определяют соответственно минимальную и максимальную скорости потока для каждой реакции, соответствующей столбцам таблицы. $S$ матрица. Эти скорости могут быть определены экспериментально, чтобы еще больше ограничить и повысить точность прогнозирования модели, или им можно задать произвольно высокое значение, указывающее на отсутствие ограничений на поток через реакцию.

Основное преимущество метода баланса потоков состоит в том, что он не требует каких-либо знаний о концентрациях метаболитов или, что более важно, о кинетике ферментов системы; предположение о гомеостазе исключает необходимость знания концентраций метаболитов в любой момент времени, пока это количество остается постоянным, и, кроме того, оно устраняет необходимость в конкретных законах скорости, поскольку предполагает, что в устойчивом состоянии нет изменений в размере метаболита. пул в системе. Одних только стехиометрических коэффициентов достаточно для математической максимизации конкретной целевой функции .

Целевая функция, по сути, является мерой того, какой вклад каждый компонент системы вносит в производство желаемого продукта. Сам продукт зависит от цели модели, но одним из наиболее распространенных примеров является исследование общей биомассы. Ярким примером успеха FBA является способность точно предсказать скорость роста прокариот E. coli при культивировании в различных условиях. В этом случае метаболическая система была оптимизирована для максимизации целевой функции биомассы. Однако эту модель можно использовать для оптимизации производства любого продукта и часто используют для определения уровня производства какого-либо биотехнологически значимого продукта. Сама модель может быть экспериментально проверена путем культивирования организмов с использованием хемостата или аналогичных инструментов, чтобы гарантировать постоянство концентрации питательных веществ. Затем измерения достижения желаемой цели можно использовать для корректировки модели.

Хорошее описание основных концепций FBA можно найти в свободно доступных дополнительных материалах к книге Edwards et al. 2001 г. который можно найти на сайте Nature. Дополнительные источники включают книгу Б. Палссона «Системная биология», посвященную этой теме. а также полезный учебник и статья Дж. Орта. В опубликованной научной литературе существует множество других источников информации об этом методе, включая Lee et al. 2006, Файст и др. 2008, и Льюис и др. 2012.

Подготовка и доработка модели

Ключевыми частями подготовки модели являются: создание метаболической сети без пробелов, добавление ограничений в модель и, наконец, добавление целевой функции (часто называемой функцией биомассы), обычно для моделирования роста моделируемого организма.

Метаболическая сеть и программные инструменты

Первые шесть реакций гликолиза подготовлены к FBA путем добавления целевой функции (красный) и импорта и экспорта питательных веществ (АТФ, АДФ, БДГ, АДГ) через границу системы (пунктирная зеленая линия).

Метаболические сети могут различаться по объему: от сетей, описывающих один путь , до клеток , тканей или организмов . Основным требованием к метаболической сети, составляющей основу сети, готовой к FBA, является отсутствие в ней пробелов. Обычно это означает, что требуется обширное ручное курирование, что делает подготовку метаболической сети для анализа баланса потоков процессом, который может занять месяцы или годы. Однако недавние достижения, такие как так называемые методы заполнения пробелов, могутсократить необходимое время до недель или месяцев.

Пакеты программного обеспечения для создания моделей FBA включают: Pathway Tools/MetaFlux , Симфени, МетНетМакер, КОБРАпи, Вырезать меня, МИОМ, или COBREXA.jl.

Обычно модели создаются в формате BioPAX или SBML, чтобы дальнейший анализ или визуализацию можно было выполнить в другом программном обеспечении, хотя это не является обязательным требованием.

Ограничения

Ключевой частью FBA является возможность добавлять ограничения на скорости потоков реакций внутри сетей, заставляя их оставаться в пределах диапазона выбранных значений. Это позволяет модели более точно имитировать реальный метаболизм. С биологической точки зрения ограничения относятся к двум подмножествам; граничные ограничения, которые ограничивают поглощение/выведение питательных веществ, и внутренние ограничения, которые ограничивают поток посредством реакций внутри организма. С математической точки зрения, применение ограничений можно рассматривать как сокращение пространства решений модели FBA. Помимо ограничений, применяемых на границах метаболической сети, ограничения могут применяться к реакциям глубоко внутри сети. Эти ограничения обычно просты; они могут ограничивать направление реакции из соображений энергии или ограничивать максимальную скорость реакции из-за конечной скорости всех реакций в природе.

Ограничения роста СМИ

Организмы и все другие метаболические системы требуют некоторого поступления питательных веществ. Обычно скорость поглощения питательных веществ определяется их доступностью (отсутствующее питательное вещество не может быть поглощено), их концентрацией и константами диффузии (более высокие концентрации быстродиффундирующих метаболитов всасываются быстрее) и методом абсорбции (например, активный транспорт или облегченная диффузия по сравнению с простой диффузией).

Если скорость абсорбции (и/или выведения) определенных питательных веществ можно измерить экспериментально, то эту информацию можно добавить в качестве ограничения скорости потока на границах метаболической модели. Это гарантирует, что питательные вещества, которые отсутствуют или не усваиваются организмом, не вступают в его метаболизм (скорость потока ограничена нулем), а также означает, что при моделировании будут соблюдаться известные скорости поглощения питательных веществ. Это обеспечивает вторичный метод проверки того, что смоделированный метаболизм имеет экспериментально проверенные свойства, а не просто математически приемлемые.

Ограничения термодинамической реакции

В принципе, все реакции обратимы, однако на практике реакции часто эффективно протекают только в одном направлении. Это может быть связано со значительно большей концентрацией реагентов по сравнению с концентрацией продуктов реакции. Но чаще всего это происходит потому, что продукты реакции имеют гораздо меньшую свободную энергию, чем реагенты, и поэтому прямое направление реакции предпочтительнее.

Для идеальных реакций

$-\infty <v_{i}<\infty \,$

Для некоторых реакций можно применить термодинамическое ограничение, подразумевающее направление (в данном случае вперед).

$0<v_{i}<\infty \,$

Реально поток через реакцию не может быть бесконечным (учитывая, что ферменты в реальной системе конечны), что означает, что

$0<v_{i}<v_{\max }\,$

Экспериментально измеренные ограничения потока

Определенные скорости потока можно измерить экспериментально ( $v_{i,m}\,$), а потоки в рамках метаболической модели могут быть ограничены в пределах некоторой ошибки ( $\varepsilon \,$), чтобы гарантировать, что эти известные скорости потока точно воспроизводятся в моделировании.

$v_{i,m}-\varepsilon <v_{i}<v_{i,m}+\varepsilon \,$

Скорость потока легче всего измерить по потреблению питательных веществ на краю сети. Измерения внутренних потоков возможны с использованием радиоактивно меченых или видимых ЯМР метаболитов.

Ограниченные метаболические модели, готовые к FBA, можно анализировать с помощью программного обеспечения, такого как набор инструментов COBRA. (доступны реализации в MATLAB и Python ), SurreyFBA, или веб-сайт FAME. Дополнительные пакеты программного обеспечения перечислены в другом месте. Недавно был проведен всесторонний обзор всего такого программного обеспечения и его функций.

Альтернатива с открытым исходным кодом доступна на R (языке программирования) в виде пакетов abcdeFBA или sybil. для выполнения FBA и других методов моделирования на основе ограничений.

Целевая функция

FBA может дать большое количество математически приемлемых решений стационарной задачи. $(S{\vec {v}}=0)$. Однако биологический интерес представляют те растворы, которые производят желаемые метаболиты в правильной пропорции. Целевая функция определяет долю этих метаболитов. Например, при моделировании роста организма целевая функция обычно определяется как биомасса. Математически это столбец в матрице стехиометрии, записи которого создают «спрос» или действуют как «приемник» для биосинтетических предшественников, таких как жирные кислоты, аминокислоты и компоненты клеточной стенки, которые присутствуют в соответствующих строках S. матрица. Эти записи представляют собой экспериментально измеренные пропорции клеточных компонентов в сухом весе. Таким образом, этот столбец становится сосредоточенной реакцией, моделирующей рост и размножение. Таким образом, точность экспериментальных измерений играет важную роль в правильном определении функции биомассы и делает результаты FBA биологически применимыми, гарантируя, что правильная пропорция метаболитов образуется в результате метаболизма.

При моделировании небольших сетей целевую функцию можно соответствующим образом изменить. Примером этого может служить изучение путей углеводного метаболизма , где целевая функция, вероятно, будет определена как определенная пропорция АТФ и НАДН и, таким образом, моделирует выработку высокоэнергетических метаболитов этим путем.

Оптимизация целевой функции/функции биомассы

Линейное программирование можно использовать для поиска единственного оптимального решения. Наиболее распространенной целью биологической оптимизации метаболической сети всего организма является выбор вектора потока. ${\vec {v}}$ который максимизирует поток за счет функции биомассы, состоящей из составляющих метаболитов организма, помещенных в стехиометрическую матрицу и обозначенных $v_{\textrm {biomass}}$ или просто $v_{b}$

$\max _{\vec {v}}\ v_{b}\qquad {\textrm {s.t.}}\qquad \mathbf {S} \,{\vec {v}}=0$

В более общем случае любая реакция может быть определена и добавлена ​​к функции биомассы либо с условием ее максимизации, либо с минимизацией, если желательно одно «оптимальное» решение. Альтернативно, в самом общем случае, вектор ${\vec {c}}$ может быть введено, что определяет взвешенный набор реакций, которые модель линейного программирования должна стремиться максимизировать или минимизировать,

$\max _{\vec {v}}\ {\vec {v}}\cdot {\vec {c}}\qquad {\textrm {s.t.}}\qquad \mathbf {S} \,{\vec {v}}=0.$

В случае наличия только одной отдельной функции/реакции биомассы в стехиометрической матрице. ${\vec {c}}$ упростится до всех нулей со значением 1 (или любым ненулевым значением) в позиции, соответствующей этой функции биомассы. Там, где было несколько отдельных целевых функций ${\vec {c}}$ упростится до всех нулей с взвешенными значениями в позициях, соответствующих всем целевым функциям.

Уменьшение пространства решений – биологические соображения для системы

Анализ нулевого пространства матриц реализован в пакетах программного обеспечения, специализирующихся на матричных операциях, таких как Matlab и Octave. Определение нулевого пространства $\scriptstyle \mathbf {S}$ сообщает нам все возможные наборы векторов потоков (или их линейных комбинаций), которые уравновешивают потоки внутри биологической сети. Преимущество такого подхода становится очевидным в биологических системах, которые описываются системами дифференциальных уравнений со многими неизвестными. Скорости в дифференциальных уравнениях выше - $v_{1}$ и $v_{2}$ - зависят от скоростей реакций основных уравнений. Скорости обычно берутся из кинетической теории Михаэлиса-Ментен , которая включает кинетические параметры ферментов, катализирующих реакции, и концентрацию самих метаболитов. Выделение ферментов из живых организмов и измерение их кинетических параметров является сложной задачей, как и измерение внутренних концентраций и констант диффузии метаболитов внутри организма. Таким образом, подход дифференциальных уравнений к метаболическому моделированию выходит за рамки современной науки для всех организмов, кроме наиболее изученных. FBA позволяет избежать этого препятствия, применяя гомеостатическое предположение, которое является достаточно приблизительным описанием биологических систем.

Хотя FBA позволяет избежать этого биологического препятствия, математическая проблема большого пространства решений остается. FBA преследует двойную цель. Точное представление биологических пределов системы и возвращение распределения потоков, наиболее близкого к естественным потокам внутри целевой системы/организма. Определенные биологические принципы могут помочь преодолеть математические трудности. Хотя стехиометрическая матрица почти всегда изначально недоопределена (это означает, что пространство решений для $\scriptstyle \mathbf {S} \,{\vec {v}}=0$ очень велик), размер пространства решений можно уменьшить и сделать его более отражающим биологию проблемы за счет применения определенных ограничений на решения.

Расширения

Успех FBA и осознание его ограничений привели к его расширениям, которые пытаются смягчить ограничения этого метода.

Анализ изменчивости потока

Визуальное и численное представление FVA во всей сети.

Оптимальное решение проблемы баланса потоков редко бывает уникальным, поскольку существует множество возможных и одинаково оптимальных решений. Анализ изменчивости потоков (FVA), встроенный в некоторые аналитические программы, возвращает границы потоков для каждой реакции, которые в сочетании с правильной комбинацией других потоков могут оценить оптимальное решение.

Визуальное и численное представление FVA в сети с нелетальным удалением.

Реакции, которые могут поддерживать низкую вариабельность потоков через них, вероятно, будут иметь более важное значение для организма, и FVA является многообещающим методом идентификации важных реакций.

Минимизация метаболической адаптации (МОМА)

При моделировании выбивания или роста среды FBA дает окончательное стационарное распределение потока. Это окончательное устойчивое состояние достигается в различных временных масштабах. Например, прогнозируемая скорость роста E. coli на глицерине в качестве основного источника углерода не соответствовала прогнозам FBA; однако при субкультивировании в течение 40 дней или 700 поколений скорость роста адаптивно развивалась в соответствии с прогнозом FBA.

Иногда представляет интерес выяснить, каков непосредственный эффект возмущения или нокаута, поскольку требуется время, чтобы произошли регуляторные изменения и организм реорганизовал потоки, чтобы оптимально использовать другой источник углерода или обойти эффект нокаутировать. MOMA предсказывает немедленное неоптимальное распределение потока после возмущения путем минимизации расстояния (евклидова) между распределением потока FBA дикого типа и распределением потока мутанта с использованием квадратичного программирования. Это приводит к задаче оптимизации формы.

$\min \ ||\mathbf {v_{w}} -\mathbf {v_{d}} ||^{2}\qquad s.t.\quad \mathbf {S} \cdot \mathbf {v_{d}} =0$

где $\mathbf {v_{w}}$ представляет распределение потока дикого типа (или невозмущенного состояния) и $\mathbf {v_{d}}$ представляет собой распределение потока при делеции гена, которое необходимо найти. Это упрощает:

$\min \ {\frac {1}{2}}\,{\mathbf {v_{d}} }^{T}\,\mathbf {I} \,\mathbf {v_{d}} +(\mathbf {-v_{w}} )\cdot \mathbf {v_{d}} \qquad s.t.\quad \mathbf {S} \cdot \mathbf {v_{d}} =0$

Это решение MOMA, которое представляет распределение потока сразу после возмущения.

Нормативная двухпозиционная минимизация (ROOM)

ROOM пытается улучшить прогноз метаболического состояния организма после нокаута гена. Это следует той же предпосылке, что и MOMA, что после нокаута организм будет пытаться восстановить распределение потока как можно ближе к дикому типу. Однако далее предполагается, что это устойчивое состояние будет достигнуто посредством серии временных метаболических изменений регуляторной сети и что организм будет пытаться свести к минимуму количество регуляторных изменений, необходимых для достижения состояния дикого типа. Однако вместо использования минимизации метрики расстояния используется метод линейного программирования смешанных целых чисел.

Динамический ФБА

Динамический FBA пытается добавить возможность изменения моделей с течением времени, тем самым в некотором смысле избегая строгого устойчивого состояния чистого FBA. Обычно этот метод включает в себя запуск моделирования FBA, изменение модели на основе результатов этого моделирования и повторный запуск моделирования. Повторяя этот процесс, со временем достигается элемент обратной связи.

Сравнение с другими методами

FBA обеспечивает менее упрощенный анализ, чем анализ узких мест, требуя при этом гораздо меньше информации о скорости реакции и гораздо менее полную реконструкцию сети, чем потребовалось бы полное динамическое моделирование. Было показано, что FBA, заполняя эту нишу, является очень полезным методом анализа метаболических возможностей клеточных систем.

Анализ узких мест

В отличие от анализа узких мест , который учитывает только точки в сети, где метаболиты производятся, но не потребляются или наоборот, FBA является истинной формой моделирования метаболической сети , поскольку он рассматривает метаболическую сеть как единое целое ( стехиометрическую матрицу ) на всех этапах. анализа. Это означает, что в модели можно воспроизвести сетевые эффекты, такие как химические реакции на удаленных путях, влияющие друг на друга. Положительная сторона неспособности анализа узких мест моделировать сетевые эффекты заключается в том, что он рассматривает каждую реакцию внутри сети изолированно и, таким образом, может предложить важные реакции в сети, даже если сеть сильно фрагментирована и содержит много пробелов.

Динамическое метаболическое моделирование

В отличие от динамического метаболического моделирования , FBA предполагает, что внутренняя концентрация метаболитов внутри системы остается постоянной с течением времени и, следовательно, не может обеспечить ничего, кроме стационарных решений. Вряд ли ФБА сможет, например, моделировать функционирование нервной клетки. Поскольку внутренняя концентрация метаболитов не учитывается в модели, возможно, что раствор FBA может содержать метаболиты в концентрации, слишком высокой, чтобы быть биологически приемлемой. Это проблема, которую, вероятно, можно было бы избежать с помощью динамического метаболического моделирования. Одним из преимуществ простоты FBA по сравнению с динамическим моделированием является то, что они гораздо менее затратны в вычислительном отношении, что позволяет моделировать большое количество возмущений в сети. Второе преимущество заключается в том, что реконструированная модель может быть существенно проще, если избежать необходимости учитывать скорости ферментов и влияние сложных взаимодействий на кинетику ферментов.

См. также

• Изотопная маркировка
• Метаболомика
• Метаболическая инженерия
• Моделирование метаболической сети