Дерево двоичных выражений
Дерево двоичных выражений — это особый вид двоичного дерева, используемый для представления выражений . Двумя распространенными типами выражений, которые может представлять дерево двоичных выражений, являются алгебраические. [1] и логическое значение . Эти деревья могут представлять выражения, содержащие как унарные , так и бинарные операторы. [1]
Как и любое двоичное дерево, каждый узел дерева двоичных выражений имеет ноль, одного или двух дочерних элементов. Эта ограниченная структура упрощает обработку деревьев выражений.
Построение дерева выражений
[ редактировать ]Пример
[ редактировать ]Ввод в постфиксной записи: ab + cde + * *Поскольку первые два символа являются операндами, создаются одноузловые деревья и указатели на них помещаются в стек. Для удобства стек будет расти слева направо.
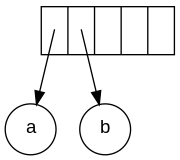
Следующий символ — «+». Он извлекает два указателя на деревья, формируется новое дерево, и указатель на него помещается в стек.
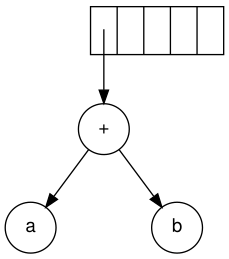
Далее читаются c, d и e. Для каждого создается одноузловое дерево, и в стек помещается указатель на соответствующее дерево.
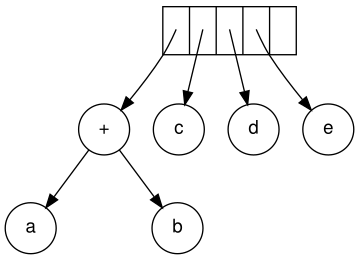
Далее считывается «+», и последние два дерева объединяются.

Теперь читается «*». Последние два указателя дерева извлекаются, и формируется новое дерево с корнем «*».

Наконец, читается последний символ. Два дерева объединяются, и в стеке остается указатель на последнее дерево. [2]
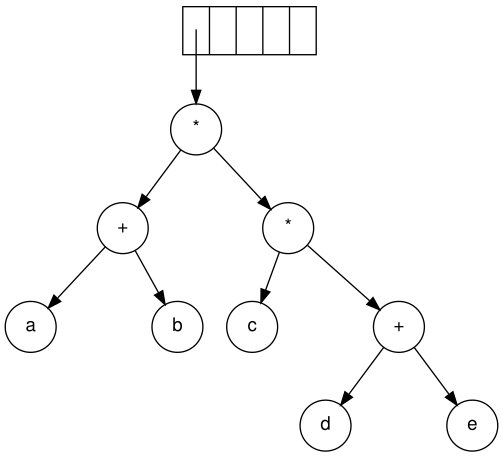
Алгебраические выражения
[ редактировать ]
Алгебраические деревья выражений представляют собой выражения, содержащие числа , переменные , а также унарные и бинарные операторы. Некоторые из распространенных операторов: × ( умножение ), ÷ ( деление ), + ( сложение ), − ( вычитание ), ^ ( возведение в степень ) и - ( отрицание ). Операторы содержатся во внутренних узлах дерева, а числа и переменные — в листовых узлах . [1] Узлы бинарных операторов имеют два дочерних узла , а унарные операторы — один дочерний узел.
Логические выражения
[ редактировать ]
Булевы выражения представляются очень похоже на алгебраические выражения, с той лишь разницей, что используются конкретные значения и операторы. Логические выражения используют true и false в качестве постоянных значений, а операторы включают в себя ( И ), ( ИЛИ ), ( НЕТ ).
См. также
[ редактировать ]- Выражение (математика)
- Термин (логика)
- Контекстно-свободная грамматика
- Дерево разбора
- Абстрактное синтаксическое дерево
Ссылки
[ редактировать ]- ^ Jump up to: а б с Бруно Р. Прейсс (1998). «Деревья выражений» . Архивировано из оригинала 19 января 2017 года . Проверено 20 декабря 2010 г.
- ^ Гопал, Арпита. Увеличение структур данных . PHI Learning, 2010, с. 353.


