Сезонность
В этой статье есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
В временных рядов данных сезонность относится к тенденциям, которые происходят через определенные регулярные промежутки времени менее года, например еженедельно, ежемесячно или ежеквартально. Сезонность может быть вызвана различными факторами, такими как погода, отпуск и праздники. [1] и состоит из периодических, повторяющихся и, как правило, регулярных и предсказуемых закономерностей на уровнях. [2] временного ряда.
Сезонным колебаниям временного ряда можно противопоставить циклические закономерности. Последнее происходит, когда данные демонстрируют подъемы и спады, не относящиеся к фиксированному периоду. Такие несезонные колебания обычно обусловлены экономическими условиями и часто связаны с «деловым циклом»; их период обычно превышает один год, а колебания обычно составляют не менее двух лет. [3]
Организации, сталкивающиеся с сезонными колебаниями, например, продавцы мороженого, часто заинтересованы в том, чтобы узнать свою производительность по сравнению с обычными сезонными колебаниями. Сезонные колебания на рынке труда можно объяснить выходом на рынок труда выпускников школ, поскольку они стремятся внести свой вклад в рабочую силу после завершения обучения. Эти регулярные изменения представляют меньший интерес для тех, кто изучает данные о занятости, чем изменения, которые происходят из-за основного состояния экономики; их внимание сосредоточено на том, как изменилась безработица среди рабочей силы, несмотря на влияние регулярных сезонных колебаний. [3]
Организациям необходимо выявлять и измерять сезонные колебания на своем рынке, чтобы помочь им планировать будущее. Это может подготовить их к временному увеличению или уменьшению потребности в рабочей силе и запасах, поскольку спрос на их продукцию или услуги колеблется в течение определенных периодов. Это может потребовать обучения, периодического обслуживания и т. д., которые можно организовать заранее. Помимо этих соображений, организациям необходимо знать, были ли наблюдаемые ими колебания больше или меньше ожидаемого значения, помимо того, что учитывают обычные сезонные колебания.
Мотивация
[ редактировать ]Существует несколько основных причин для изучения сезонных изменений:
- Описание сезонного эффекта позволяет лучше понять влияние этого компонента на конкретный ряд.
- После установления сезонной закономерности можно применить методы ее исключения из временного ряда для изучения влияния других компонентов, таких как циклические и нерегулярные изменения. Такое устранение сезонного эффекта называется десезонализацией или сезонной корректировкой данных.
- Использовать прошлые закономерности сезонных изменений для содействия прогнозированию и предсказанию будущих тенденций, например, климатических норм .
Обнаружение
[ редактировать ]следующие графические методы Для обнаружения сезонности можно использовать :
- График последовательности выполнения часто показывает сезонность.

График сезонности потребления электроэнергии в США - Сезонный график покажет перекрывающиеся данные каждого сезона. [4]
- График сезонных подсерий — это специализированный метод отображения сезонности.
- Множественные коробчатые диаграммы можно использовать в качестве альтернативы сезонным графикам подрядов для выявления сезонности.
- График автокорреляции (ACF) и спектральный график могут помочь определить сезонность.
Действительно хороший способ найти периодичность, включая сезонность, в любом регулярном ряде данных — сначала удалить любую общую тенденцию, а затем проверить временную периодичность. [5]
График последовательности прогонов — рекомендуемый первый шаг для анализа любого временного ряда. Хотя на этом графике иногда можно указать сезонность, сезонность более четко отображается на графике сезонных подрядов или коробчатом графике. График сезонных подсерий отлично показывает как сезонные различия (между групповыми закономерностями), так и внутригрупповые закономерности. Ящичковая диаграмма довольно хорошо показывает сезонную разницу (между групповыми моделями), но не проявляется внутри групповых моделей. Однако для больших наборов данных коробчатую диаграмму обычно легче читать, чем диаграмму сезонных подрядов.
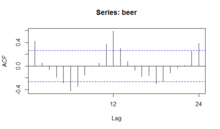
Сезонный график, график сезонных подсерий и коробчатая диаграмма предполагают, что сезонные периоды известны. В большинстве случаев аналитик действительно это знает. Например, для ежемесячных данных период равен 12, поскольку в году 12 месяцев. Однако, если период неизвестен, может помочь график автокорреляции. Если существует значительная сезонность, график автокорреляции должен показывать всплески с лагами, равными периоду. Например, для ежемесячных данных, если существует эффект сезонности, мы ожидаем увидеть значительные пики на лаге 12, 24, 36 и т. д. (хотя интенсивность может уменьшаться по мере дальнейшего продвижения).
График автокорреляции (ACF) можно использовать для определения сезонности, поскольку он рассчитывает разницу (остаточную сумму) между значением Y и значением с задержкой Y. Результат дает несколько точек, в которых два значения близки друг к другу (без сезонности). но есть и другие моменты, где есть большие расхождения. Эти точки указывают на уровень сезонности данных.
С полурегулярными циклическими изменениями можно справиться с помощью оценки спектральной плотности .
Расчет
[ редактировать ]Сезонные колебания измеряются с помощью индекса, называемого сезонным индексом. Это среднее значение, которое можно использовать для сравнения фактического наблюдения с тем, каким оно было бы, если бы не было сезонных колебаний. К каждому периоду временного ряда в течение года присваивается значение индекса. Это означает, что если рассматривать ежемесячные данные, то имеется 12 отдельных сезонных индексов, по одному на каждый месяц. Следующие методы используют сезонные индексы для измерения сезонных изменений данных временных рядов.
- Метод простых средних
- отношения к тренду Метод
- отношения к скользящему среднему Метод
- Метод связи родственников
Метод простых средних
[ редактировать ]Измерение сезонных колебаний с использованием метода отношения к скользящему среднему дает индекс для измерения степени сезонных колебаний во временном ряду. Индекс основан на среднем значении 100, при этом степень сезонности измеряется отклонениями от базовой точки. Например, если мы посмотрим на аренду отелей на зимнем курорте, мы обнаружим, что индекс зимнего квартала равен 124. Значение 124 указывает на то, что 124 процента средней квартальной арендной платы приходится на зимний период. Если руководство отеля зафиксирует 1436 арендных плат за весь прошлый год, то средняя квартальная арендная плата составит 359= (1436/4). Поскольку индекс зимнего квартала равен 124, мы оцениваем количество зимних квартир следующим образом:
359*(124/100)=445;
Здесь 359 — это средняя квартальная арендная плата. 124 — индекс зимнего квартала. 445 Сезонная аренда на зимний квартал.
Этот метод еще называют методом процентного скользящего среднего . В этом методе исходные значения данных во временном ряду выражаются в процентах от скользящих средних. Шаги и таблицы приведены ниже.
Метод отношения к тренду
[ редактировать ]- Найдите центрированные 12 месячных (или 4 квартальных) скользящих средних исходных значений данных во временном ряду .
- Выразите каждое исходное значение данных временного ряда в процентах от соответствующих центрированных значений скользящего среднего, полученных на шаге (1). Другими словами, в мультипликативной модели временных рядов мы получаем (Исходные значения данных) / (Значения тренда) × 100 = ( T × C × S × I ) / ( T × C ) × 100 = ( S × I ) × 100.
Это означает, что отношение к скользящему среднему отражает сезонные и нерегулярные компоненты. - Расположите эти проценты по месяцам или кварталам данных лет. Найдите средние значения за все месяцы или кварталы данных лет.
- Если сумма этих индексов не равна 1200 (или 400 для квартальных показателей), умножьте ее на поправочный коэффициент = 1200/(сумма месячных индексов). В противном случае средние значения за 12 месяцев будут рассматриваться как сезонные индексы.
Метод отношения к скользящему среднему
[ редактировать ]Рассчитаем сезонный индекс методом отношения к скользящему среднему по следующим данным:
| Год/Кварталы | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1996 | 75 | 60 | 54 | 59 |
| 1997 | 86 | 65 | 63 | 80 |
| 1998 | 90 | 72 | 66 | 85 |
| 1999 | 100 | 78 | 72 | 93 |
Теперь расчеты для 4 квартальных скользящих средних и отношения к скользящим средним показаны в таблице ниже.
| Год | Четверть | Исходные значения (Y) | 4 цифры скользящего итога | 4-значная скользящая средняя | 2 цифры скользящего итога | 2-значное скользящее среднее (T) | Отношение к скользящей средней (%)(Y)/ (T)*100 |
|---|---|---|---|---|---|---|---|
| 1996 | 1 | 75 | — | — | — | ||
| — | — | ||||||
| 2 | 60 | — | — | — | |||
| 248 | 62.00 | ||||||
| 3 | 54 | 126.75 | 63.375 | 85.21 | |||
| 259 | 64.75 | ||||||
| 4 | 59 | 130.75 | 65.375 | 90.25 | |||
| 264 | 66.00 | ||||||
| 1997 | 1 | 86 | 134.25 | 67.125 | 128.12 | ||
| 273 | 68.25 | ||||||
| 2 | 65 | 141.75 | 70.875 | 91.71 | |||
| 294 | 73.50 | ||||||
| 3 | 63 | 148.00 | 74.00 | 85.13 | |||
| 298 | 74.50 | ||||||
| 4 | 80 | 150.75 | 75.375 | 106.14 | |||
| 305 | 76.25 | ||||||
| 1998 | 1 | 90 | 153.25 | 76.625 | 117.45 | ||
| 308 | 77.00 | ||||||
| 2 | 72 | 155.25 | 77.625 | 92.75 | |||
| 313 | 78.25 | ||||||
| 3 | 66 | 159.00 | 79.50 | 83.02 | |||
| 323 | 80.75 | ||||||
| 4 | 85 | 163.00 | 81.50 | 104.29 | |||
| 329 | 82.25 | ||||||
| 1999 | 1 | 100 | 166.00 | 83.00 | 120.48 | ||
| 335 | 83.75 | ||||||
| 2 | 78 | 169.50 | 84.75 | 92.03 | |||
| 343 | 85.75 | ||||||
| 3 | 72 | — | — | — | |||
| — | — | ||||||
| 4 | 93 | — | — | — | |||
| Годы/Кварталы | 1 | 2 | 3 | 4 | Общий |
|---|---|---|---|---|---|
| 1996 | — | — | 85.21 | 90.25 | |
| 1997 | 128.12 | 91.71 | 85.13 | 106.14 | |
| 1998 | 117.45 | 92.75 | 83.02 | 104.29 | |
| 1999 | 120.48 | 92.04 | — | — | |
| Общий | 366.05 | 276.49 | 253.36 | 300.68 | |
| Сезонное среднее значение | 122.01 | 92.16 | 84.45 | 100.23 | 398.85 |
| Скорректированное среднее сезонное значение | 122.36 | 92.43 | 84.69 | 100.52 | 400 |
Сейчас сумма средних сезонных значений составляет 398,85. Следовательно, соответствующий поправочный коэффициент будет равен 400/398,85 = 1,00288. Каждое среднее сезонное значение умножается на поправочный коэффициент 1,00288, чтобы получить скорректированные сезонные индексы, как показано в таблице выше.
Метод связи родственников
[ редактировать ]1. В аддитивной модели временных рядов сезонная составляющая оценивается как:
- S знак равно Y – ( Т + С + я )
где
- S : Сезонные значения.
- Y : Фактические значения данных временного ряда.
- T : тренда Значения
- C : Циклические значения
- Я : Нестандартные значения.
2. В мультипликативной модели временных рядов сезонная составляющая выражается в соотношениях и процентах как
- Сезонный эффект ;
Однако на практике удаление тренда из временных рядов делается для того, чтобы получить .
Это делается путем деления обеих сторон по значениям тренда T так, что .
3. Десезонные данные временных рядов будут иметь только трендовые ( T ), циклические ( C ) и нерегулярные ( I ) компоненты и выражаются как:
- Мультипликативная модель:
- Аддитивная модель : Y – S = ( T + S + C + I ) – S = T + C + I
Моделирование
[ редактировать ]Совершенно регулярные циклические изменения во временных рядах можно рассматривать при анализе временных рядов с использованием синусоидальной модели с одной или несколькими синусоидами , длина периода которых может быть известна или неизвестна в зависимости от контекста. С менее регулярными циклическими изменениями можно справиться, используя специальную форму модели ARIMA , которая может быть структурирована так, чтобы полуявно рассматривать циклические изменения. Такие модели представляют циклостационарные процессы .
Другой метод моделирования периодической сезонности — использование пар членов Фурье. Подобно использованию синусоидальной модели, члены Фурье, добавляемые в модели регрессии, используют синусоидальные и косинусоидальные члены для имитации сезонности. Однако сезонность такой регрессии будет представлена как сумма синусоидальных или косинусоидальных членов, а не одного синусоидального или косинусоидального члена в синусоидальной модели. Любую периодическую функцию можно аппроксимировать с помощью членов Фурье.
Разницу между синусоидальной моделью и регрессией с членами Фурье можно упростить, как показано ниже:
Синусоидальная модель:
Регрессия с условиями Фурье:
Сезонная корректировка
[ редактировать ]Сезонная корректировка или десезонализация — это любой метод удаления сезонной составляющей временного ряда . Полученные в результате сезонно скорректированные данные используются, например, при анализе или составлении отчетов о несезонных тенденциях в течение продолжительности, значительно превышающей сезонный период. Соответствующий метод сезонной корректировки выбирается на основе конкретного взгляда на разложение временных рядов на компоненты, обозначенные такими названиями, как «тренд», «циклический», «сезонный» и «нерегулярный», включая то, как они взаимодействуют с друг друга. Например, такие компоненты могут действовать аддитивно или мультипликативно. Таким образом, если сезонная составляющая действует аддитивно, метод корректировки имеет два этапа:
- оценить сезонную составляющую вариаций временного ряда, обычно в форме, имеющей нулевое среднее значение по ряду;
- вычтите расчетную сезонную составляющую из исходного временного ряда, оставив сезонно скорректированный ряд: . [3]
Если это мультипликативная модель, величина сезонных колебаний будет зависеть от уровня, что более вероятно для экономических рядов. [3] С учетом сезонности мультипликативное разложение с учетом сезонных колебаний можно записать как ; при этом исходный временной ряд делится на предполагаемую сезонную составляющую.
Мультипликативную модель можно преобразовать в аддитивную модель, взяв журнал временного ряда;
SA Мультипликативное разложение:
Ведение журнала временного ряда мультипликативной модели: [3]
Одна конкретная реализация сезонной корректировки представлена X-12-ARIMA .
В регрессионном анализе
[ редактировать ]В регрессионном анализе, таком как обычный метод наименьших квадратов , где сезонно изменяющаяся зависимая переменная находится под влиянием одной или нескольких независимых переменных , сезонность можно учитывать и измерять, включая n -1 фиктивную переменную , по одной для каждого сезона, за исключением произвольной переменной. выбранный эталонный сезон, где n — количество сезонов (например, 4 в случае метеорологических сезонов, 12 в случае месяцев и т. д.). Каждой фиктивной переменной присваивается значение 1, если точка данных взята из указанного в фиктивной переменной сезона, и 0 в противном случае. Затем прогнозируемое значение зависимой переменной для эталонного сезона вычисляется на основе остальной части регрессии, а для любого другого сезона оно вычисляется с использованием остальной части регрессии и путем вставки значения 1 для фиктивной переменной для этого сезона.
Связанные шаблоны
[ редактировать ]Важно отличать сезонные закономерности от связанных закономерностей. Сезонный характер возникает, когда на временной ряд влияет сезон или время года, например годовой, полугодовой, квартальный и т. д.Циклический паттерн , или просто цикл , возникает, когда данные повышаются и падают в другие периоды, т. е. намного более длительные (например, десятилетние ) или намного более короткие (например, еженедельные ), чем сезонные.Квазипериодичность — это более общая, нерегулярная периодичность.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ «Сезонность» . |title=Влияющие факторы|
- ^ «Архивная копия» . Архивировано из оригинала 18 мая 2015 г. Проверено 13 мая 2015 г.
{{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка ) - ^ Jump up to: а б с д и 6.1 Компоненты временных рядов — OTexts .
- ^ 2.1 Графика — OTexts .
- ^ «Временные ряды. Какой метод можно использовать для обнаружения сезонности данных?» . Крест проверен .
Дальнейшее чтение
[ редактировать ]- Франсес, Филип Ганс (1996). Периодичность и стохастические тенденции в экономических временных рядах . Нью-Йорк: Издательство Оксфордского университета. ISBN 0-19-877454-0 .
- Гайселс, Эрик; Осборн, Дениз Р. (2001). Эконометрический анализ сезонных временных рядов . Кембридж: Издательство Кембриджского университета. ISBN 0-521-56588-Х .
- Хиллеберг, Свенд (1986). Сезонность в регрессии . Орландо: Академическая пресса. ISBN 0-12-363455-5 .
- Гайндман, Роб Дж.; Атансопулос, Джордж (2021). Прогнозирование: практика и принципы (3-е изд.). ISBN 978-0-9875071-3-6 .
Внешние ссылки
[ редактировать ] СМИ, связанные с сезонностью , на Викискладе?
СМИ, связанные с сезонностью , на Викискладе? - Сезонность в электронном справочнике по статистическим методам NIST/SEMATECH
![]() В этой статье использованы общедоступные материалы из Электронный справочник NIST/SEMATECH по статистическим методам . Национальный институт стандартов и технологий .
В этой статье использованы общедоступные материалы из Электронный справочник NIST/SEMATECH по статистическим методам . Национальный институт стандартов и технологий .











