Бараньи волны

Волны Лэмба распространяются в твердых пластинах или сферах. Это упругие волны , движение частиц которых лежит в плоскости, содержащей направление распространения волны и направление, перпендикулярное пластине. В 1917 году английский математик Гораций Ламб опубликовал свой классический анализ и описание акустических волн этого типа. Их свойства оказались достаточно сложными. Бесконечная среда поддерживает только две волновые моды, движущиеся с уникальными скоростями; но пластины поддерживают два бесконечных набора волн Лэмба, скорости которых зависят от соотношения между длиной волны и толщиной пластины.

С 1990-х годов понимание и использование волн Лэмба значительно продвинулись благодаря быстрому увеличению доступности вычислительных мощностей. Теоретические формулировки Лэмба нашли существенное практическое применение, особенно в области неразрушающего контроля.

Термин «волны Рэлея-Лэмба» охватывает волну Рэлея , тип волны, которая распространяется вдоль одной поверхности. Волны Рэлея и Лэмба ограничены упругими свойствами поверхности (поверхностей), которая их направляет.

Рисунок 1: Верхний и нижний соответственно:
Расширенный (S ₀ ) режим с $d/\lambda =0.6$.
Гибкий (A ₀ ) режим с $d/\lambda =0.3$.
(Это упрощенный рисунок. Он основан только на компоненте движения z , поэтому не отображает точно искажение пластины.)

Характеристические уравнения Лэмба

В целом упругие волны в твердых материалах руководствуются границами средств массовой информации, в которых они распространяются. Подход к распространению направленных волн, широко используемый в физической акустике, заключается в поиске синусоидальных решений волнового уравнения для линейных упругих волн с учетом граничных условий, представляющих геометрию конструкции. Это классическая проблема собственных значений .

Волны в пластинах были одними из первых направленных волн, которые были проанализированы таким образом. Анализ был разработан и опубликован в 1917 году. Гораций Ламб , лидер математической физики своего времени.

Уравнения Лэмба были получены путем установления формализма для твердой пластины, имеющей бесконечную протяженность в направлениях x и y и толщину d в направлении z . Постулировались синусоидальные решения волнового уравнения , имеющие x- и z-смещения вида

$\xi =A_{x}f_{x}(z)e^{i(\omega t-kx)}\quad \quad (1)$

$\zeta =A_{z}f_{z}(z)e^{i(\omega t-kx)}\quad \quad (2)$

Эта форма представляет собой синусоидальные волны, распространяющиеся в направлении x с длиной волны 2π/k и частотой ω/2π. Смещение является функцией x , z , t только ; нет смещения в направлении y и никаких изменений каких-либо физических величин в направлении y .

Физическим граничным условием для свободных поверхностей пластины является то, что составляющая напряжения в направлении z при z = +/- d /2 равна нулю.Применяя эти два условия к формализованным выше решениям волнового уравнения, можно найти пару характеристических уравнений. Это:

${\frac {\tanh(\beta d/2)}{\tanh(\alpha d/2)}}={\frac {4\alpha \beta k^{2}}{(k^{2}+\beta ^{2})^{2}}}\ \quad \quad \quad \quad (3)$

для симметричных режимов и

${\frac {\tanh(\beta d/2)}{\tanh(\alpha d/2)}}={\frac {(k^{2}+\beta ^{2})^{2}}{4\alpha \beta k^{2}}}\ \quad \quad \quad \quad (4)$

для несимметричных режимов, где

$\alpha ^{2}=k^{2}-{\frac {\omega ^{2}}{c_{l}^{2}}}\quad \quad {\text{and}}\quad \quad \beta ^{2}=k^{2}-{\frac {\omega ^{2}}{c_{t}^{2}}}.$

В этих уравнениях присуща связь между угловой частотой ω и волновым числом k. Численные методы используются для нахождения фазовой скорости c _p = fλ = ω/k и групповой скорости c _g = dω / dk как функций d / λ или fd . c _l и c _t — скорости продольной и поперечной волн соответственно.

Решение этих уравнений также раскрывает точную форму движения частицы, которую уравнения (1) и (2) представляют только в общей форме. Найдено, что уравнение (3) порождает семейство волн, движение которых симметрично относительно средней плоскости пластины (плоскости z = 0), а уравнение (4) порождает семейство волн, движение которых антисимметрично относительно средняя плоскость. На рисунке 1 изображен член каждой семьи.

Характеристические уравнения Лэмба были установлены для волн, распространяющихся в бесконечной пластине — однородном изотропном твердом теле, ограниченном двумя параллельными плоскостями, за пределами которых никакая волновая энергия не может распространяться. Формулируя свою задачу, Лэмб ограничил компоненты движения частиц направлением нормали к пластине ( направление z ) и направлением распространения волн ( направление x ). По определению, волны Лэмба не имеют движения частиц в направлении y . Движение в направлении y в пластинах происходит в так называемых SH-модах или поперечно-горизонтальных волновых модах. Они не имеют движения в направлениях x или z и, таким образом, дополняют моды волн Лэмба. Эти два типа волн являются единственными типами волн, которые могут распространяться с прямыми бесконечными волновыми фронтами в пластине, как определено выше.

Дисперсия скорости, присущая характеристическим уравнениям

Дисперсионные кривые свободных волн Лэмба для двух различных коэффициентов Пуассона $\sigma$. По оси X показано произведение угловой частоты. $\omega$ и толщина пластины $d$ нормированная на скорость поперечной волны $v_{s}$. По оси Y показана фазовая скорость. $v$ волны Лэмба, нормированной на скорость поперечной волны. Для высоких частот $S_{0}$ и $A_{0}$ моды имеют скорость волны Рэлея, составляющую примерно 92 % скорости поперечной волны.

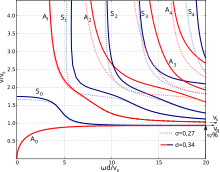
Волны Лэмба демонстрируют дисперсию скоростей; то есть скорость их распространения c зависит от частоты (или длины волны), а также от упругих постоянных и плотности материала. Это явление имеет центральное значение для изучения и понимания волнового поведения в плитах. Физически ключевым параметром является отношение толщины пластины d к длине волны. $\lambda$. Это соотношение определяет эффективную жесткость пластины и, следовательно, скорость волны. В технологических приложениях используется более практичный параметр, который легко получить из этого, а именно произведение толщины и частоты:

$f\cdot d={\frac {d\cdot c}{\lambda }},$

поскольку для всех волн

$c=f\lambda .$

Связь между скоростью и частотой (или длиной волны) заложена в характеристических уравнениях. В случае пластины эти уравнения непросты и их решение требует численных методов. Это была неразрешимая проблема до появления цифрового компьютера, спустя сорок лет после оригинальной работы Лэмба. Публикация компьютерных «дисперсионных кривых» Викторова. в бывшем Советском Союзе Файерстоун, за ним Уорлтон в Соединенных Штатах, и, в конечном итоге, многие другие привнесли теорию волн Лэмба в сферу практического применения. Бесплатный «Калькулятор дисперсии» (DC) Программное обеспечение позволяет рассчитывать дисперсионные диаграммы для изотропных пластин и многослойных анизотропных образцов. Экспериментальные формы сигналов, наблюдаемые в пластинах, можно понять, интерпретируя их со ссылкой на дисперсионные кривые.

Дисперсионные кривые — графики, показывающие взаимосвязь между скоростью волны, длиной волны и частотой в дисперсионных системах — могут быть представлены в различных формах. Форма, которая дает наибольшее понимание основополагающей физики, имеет $\omega$ (угловая частота) по оси y и k (волновое число) по оси x . Форма, использованная Викторовым, которая привела волны Лэмба в практическое использование, имеет скорость волны по оси y и $d/\lambda$, отношение толщины/длины волны, на оси x . Наиболее практичная форма из всех, в которой заслуга принадлежит Дж. и Х. Крауткремерам, а также Флойду Файерстоуну (который, кстати, придумал термин «волны Лэмба»), имеет скорость волны по оси y и fd , произведение частоты на толщину по оси x .

Характеристические уравнения Лэмба указывают на существование двух целых семейств синусоидальных волновых мод в бесконечных пластинах шириной $d$. Это контрастирует с ситуацией в неограниченных средах, где есть только две волновые моды: продольная волна и поперечная или поперечная волна . Как и в волнах Рэлея, которые распространяются вдоль одиночных свободных поверхностей, движение частиц в волнах Лэмба является эллиптическим, причем его компоненты x и z зависят от глубины внутри пластины. В одном семействе режимов движение симметрично относительно плоскости средней толщины. В другом семействе он антисимметричен.Явление дисперсии скоростей приводит к богатому разнообразию экспериментально наблюдаемых форм сигналов при распространении акустических волн в пластинах. Именно групповая скорость c _g , а не вышеупомянутая фазовая скорость c или c _p , определяет модуляции, наблюдаемые в наблюдаемой форме волны. Внешний вид сигналов критически зависит от диапазона частот, выбранного для наблюдения. Режимы изгиба и растяжения относительно легко распознать, и это пропагандируется как метод неразрушающего контроля .

Моды нулевого порядка

Отдельного внимания заслуживают симметричные и антисимметричные моды нулевого порядка. Эти моды имеют «зарождающиеся частоты» равные нулю. Таким образом, это единственные моды, которые существуют во всем частотном спектре от нуля до бесконечно высоких частот. В низкочастотном диапазоне (т. е. когда длина волны превышает толщину пластины) эти моды часто называют «модой растяжения» и «модой изгиба» соответственно. Эти термины описывают природу движения и упругую жесткость, определяющую скорости распространения. Эллиптическое движение частицы происходит в основном в плоскости пластины для симметричной моды растяжения и перпендикулярно плоскости пластины для антисимметричной моды изгиба. Эти характеристики изменяются при более высоких частотах.

Эти две моды являются наиболее важными, потому что (а) они существуют на всех частотах и ​​(б) в большинстве практических ситуаций они несут больше энергии, чем моды более высокого порядка.

Симметричная мода нулевого порядка (обозначенная S ₀ ) распространяется со «скоростью пластины» в низкочастотном режиме, где ее правильно называют «расширенной модой». В этом режиме пластина растягивается в направлении распространения и сжимается соответственно в направлении толщины. По мере увеличения частоты и длины волны, сравнимой с толщиной пластины, искривление пластины начинает оказывать существенное влияние на ее эффективную жесткость. Фазовая скорость падает плавно, тогда как групповая скорость несколько резко падает к минимуму. Еще на более высоких частотах и ​​фазовая скорость, и групповая скорость сходятся к скорости волны Рэлея - фазовая скорость сверху и групповая скорость снизу.

В низкочастотном пределе для режима растяжения z- и x-компоненты поверхностного смещения находятся в квадратуре, а отношение их амплитуд определяется выражением: $${\frac {a_{z}}{a_{x}}}={\frac {\pi \nu }{(1-\nu )}}.{\frac {d}{\lambda }}$$где $\nu$ – коэффициент Пуассона.

Антисимметричная мода нулевого порядка (обозначенная A ₀ ) обладает высокой дисперсией в низкочастотном режиме, где ее правильно называют «изгибной модой» или «изгибной модой». Для очень низких частот (очень тонкие пластины) фазовая и групповая скорости пропорциональны квадратному корню из частоты; групповая скорость в два раза больше фазовой скорости. Эта простая зависимость является следствием зависимости жесткости/толщины тонких пластин при изгибе. На более высоких частотах, когда длина волны уже ненамного превышает толщину пластины, эти соотношения нарушаются. Фазовая скорость возрастает все менее быстро и в высокочастотном пределе сходится к скорости волны Рэлея. Групповая скорость проходит через максимум, несколько быстрее скорости поперечной волны, когда длина волны примерно равна толщине пластины. Затем она сходится сверху к скорости волны Рэлея в пределе высоких частот.

В экспериментах, которые позволяют возбуждать и обнаруживать как режимы растяжения, так и режимы изгиба, режим растяжения часто проявляется как предшественник изгибного режима с более высокой скоростью и меньшей амплитудой. Изгибная мода легче возбуждается и часто несет в себе большую часть энергии.

Режимы высшего порядка

С повышением частоты помимо мод нулевого порядка появляются волновые моды более высокого порядка. Каждая мода высшего порядка «рождается» на резонансной частоте пластины и существует только выше этой частоты. Например, в Стальная пластина толщиной 3 ⁄ дюйма (19 мм) при частоте 200 кГц присутствуют первые четыре моды волны Лэмба, а при 300 кГц — первые шесть. Первые несколько мод более высокого порядка можно отчетливо наблюдать при благоприятных экспериментальных условиях. При менее благоприятных условиях они перекрываются и не могут быть различимы.

Моды Лэмба более высокого порядка характеризуются узловыми плоскостями внутри пластины, параллельными ее поверхностям. Каждая из этих мод существует только выше определенной частоты, которую можно назвать ее «зарождающейся частотой». Ни для одного из режимов нет верхнего предела частоты. Возникающие частоты можно представить как резонансные частоты продольных или поперечных волн, распространяющихся перпендикулярно плоскости пластины, т.е.

$d={\frac {n\lambda }{2}}\quad \quad {\text{or}}\quad \quad f={\frac {nc}{2d}}$

где n — любое положительное целое число. Здесь c может быть либо скоростью продольной волны, либо скоростью поперечной волны, и для каждого результирующего набора резонансов соответствующие моды волны Лэмба попеременно симметричны и антисимметричны. Взаимодействие этих двух наборов приводит к появлению структуры зарождающихся частот, которая на первый взгляд кажется нерегулярной. Например, в стальной пластине толщиной 3/4 дюйма (19 мм), имеющей продольную скорость и скорость сдвига 5890 м/с и 3260 м/с соответственно, частоты возникновения антисимметричных мод A ₁ и A ₂ составляют 86 кГц и 310 кГц. соответственно, тогда как возникающие частоты симметричных мод S1 _, S2 _и S3 _{составляют} 155 кГц, 172 кГц и 343 кГц соответственно.

На своей зарождающейся частоте каждая из этих мод имеет бесконечную фазовую скорость и нулевую групповую скорость. В высокочастотном пределе фазовая и групповая скорости всех этих мод сходятся к скорости поперечной волны. Из-за этих сходений рэлеевская и сдвиговая скорости (которые очень близки друг к другу) имеют большое значение в толстых пластинах. Проще говоря, с точки зрения материала, имеющего величайшее инженерное значение, большая часть энергии высокочастотных волн, которая распространяется на большие расстояния в стальных пластинах, распространяется со скоростью 3000–3300 м/с.

Движение частиц в модах волны Лэмба в целом является эллиптическим, имеющим компоненты как перпендикулярные, так и параллельные плоскости пластины. Эти компоненты находятся в квадратуре, т.е. имеют разность фаз 90°. Относительная величина компонентов является функцией частоты. Для некоторых изделий «частота-толщина» амплитуда одного компонента проходит через ноль, так что движение полностью перпендикулярно или параллельно плоскости пластины. Для частиц на поверхности пластины эти условия возникают, когда фазовая скорость волны Лэмба равна √ 2 c _t или только для симметричных мод c _l соответственно. Эти соображения направленности важны при рассмотрении излучения акустической энергии от пластин в соседние жидкости.

Движение частицы также полностью перпендикулярно или полностью параллельно плоскости пластины на начальной частоте моды. Вблизи возникающих частот мод, соответствующих продольно-волновым резонансам пластины, движение их частиц будет почти полностью перпендикулярно плоскости пластины; и вблизи резонансов поперечной волны — параллельно.

Дж. и Х. Крауткремеры отметили Волны Лэмба можно представить как систему продольных и поперечных волн, распространяющихся под подходящим углом поперек и вдоль пластины. Эти волны отражаются, преобразуют моды и объединяются, образуя устойчивую когерентную волновую картину. Для формирования этой когерентной волновой картины толщина пластины должна соответствовать углам распространения и длинам волн лежащих в основе продольных и поперечных волн; это требование приводит к соотношениям дисперсии скоростей.

Волны Лэмба с цилиндрической симметрией; пластинчатые волны от точечных источников

Хотя анализ Лэмба предполагал прямой волновой фронт, было показано, что что те же характеристические уравнения применимы к цилиндрическим пластинчатым волнам (т. е. волнам, распространяющимся наружу от линейного источника, причем линия лежит перпендикулярно пластине). Разница в том, что в то время как «несущая» для прямого волнового фронта представляет собой синусоиду, «несущая» для осесимметричной волны представляет собой функцию Бесселя. Функция Бесселя учитывает сингулярность в источнике, а затем сходится к синусоидальному поведению на больших расстояниях.

Эти цилиндрические волны являются собственными функциями, из которых можно составить реакцию пластины на точечные возмущения. Таким образом, реакция пластины на точечное возмущение может быть выражена как комбинация волн Лэмба и затухающих членов в ближнем поле. Общий результат можно условно представить как узор из круговых волновых фронтов, похожих на рябь от камня, брошенного в пруд, но более глубоко меняющихся по форме по мере продвижения наружу. Теория волн Лэмба относится только к движению в направлении (r, z); поперечное движение - это отдельная тема.

Управляемые волны Лэмба

Эта фраза довольно часто встречается при неразрушающем контроле. «Направляемые волны Лэмба» можно определить как волны Лэмба, которые направляются конечными размерами реальных тестовых объектов. Добавление приставки «направляемая» к фразе «волна Лэмба» означает, таким образом, признание того, что бесконечной пластины Лэмба в действительности нигде нет.

В действительности мы имеем дело с конечными пластинами или пластинами, завернутыми в цилиндрические трубы или сосуды, или пластинами, нарезанными тонкими полосками, и т. д. Теория волн Лэмба часто дает очень хорошее объяснение большей части волнового поведения таких структур. Это не даст идеального отчета, и именно поэтому фраза «Направляемые волны Лэмба» более уместна с практической точки зрения, чем «Волны Лэмба». Один вопрос заключается в том, как реальная геометрия детали повлияет на скорости и формы волн Лэмба. Например, скорость волны Лэмба в тонком цилиндре будет незначительно зависеть от радиуса цилиндра и от того, движется ли волна вдоль оси или по окружности. Другой вопрос, какие совершенно иные акустические характеристики и волновые режимы могут присутствовать в реальной геометрии детали. Например, цилиндрическая труба имеет изгибные режимы, связанные с телесным движением всей трубы, сильно отличающиеся от изгибного режима Лэмба стенки трубы.

Волны Лэмба при ультразвуковом контроле

Целью ультразвукового контроля обычно является поиск и характеристика отдельных дефектов испытуемого объекта. Такие дефекты обнаруживаются, когда они отражают или рассеивают падающую волну и отраженная или рассеянная волна достигает поискового блока с достаточной амплитудой.

Традиционно ультразвуковой контроль проводится волнами, длина волны которых намного короче размеров контролируемой детали. В этом высокочастотном режиме ультразвуковой инспектор использует волны, которые приближаются к модам продольных и поперечных волн бесконечной среды, зигзагообразно перемещаясь по толщине пластины и обратно. Хотя пионеры волны Лэмба работали над приложениями неразрушающего контроля и привлекли внимание к теории, широкое распространение она получила только в 1990-х годах, когда компьютерные программы для расчета дисперсионных кривых и связи их с экспериментально наблюдаемыми сигналами стали гораздо более широко доступными. Эти вычислительные инструменты, наряду с более широким пониманием природы волн Лэмба, позволили разработать методы неразрушающего контроля с использованием длин волн, сравнимых или превышающих толщину пластины. На этих более длинных волнах затухание волны меньше, поэтому дефекты можно обнаружить на больших расстояниях.

Основная проблема и умение использовать волны Лэмба для ультразвукового контроля - это генерация определенных мод на определенных частотах, которые будут хорошо распространяться и давать чистые отраженные «эхо». Это требует тщательного контроля возбуждения. Методы для этого включают использование гребенчатых преобразователей, клиньев, волн от жидких сред и электромагнитно-акустических преобразователей ( ЭМАП ).

Волны Лэмба в акусто-ультразвуковом контроле

Акусто-ультразвуковой контроль отличается от ультразвукового контроля тем, что он был задуман как средство оценки повреждений (и других свойств материала), распределенных по значительным площадям, а не индивидуальной характеристики дефектов. Волны Лэмба хорошо подходят для этой концепции, поскольку они облучают всю толщину пластины и распространяются на значительные расстояния с постоянным характером движения.

Волны Лэмба при испытаниях акустической эмиссии

Акустическая эмиссия использует гораздо более низкие частоты, чем традиционный ультразвуковой контроль, и обычно ожидается, что датчик обнаружит активные дефекты на расстояниях до нескольких метров. Большая часть конструкций, обычно испытываемых акустической эмиссией, изготавливается из листовой стали: резервуары, сосуды под давлением, трубы и т.д. Таким образом, теория волн Лэмба является основной теорией для объяснения форм сигналов и скоростей распространения, которые наблюдаются при проведении испытаний акустической эмиссии. Анализ сигналов акустической эмиссии с помощью теории направленных волн называется модальной акустической эмиссией (MAE). Существенного повышения точности определения местоположения источника (основной метод тестирования АЭ) можно достичь за счет хорошего понимания и умелого использования знаний о волнах Лэмба.

Ультразвуковой и акустико-эмиссионный контроль в сравнении

Произвольное механическое возбуждение, приложенное к пластине, создаст множество волн Лэмба, несущих энергию в широком диапазоне частот. Так обстоит дело с волной акустической эмиссии. При испытаниях акустической эмиссии задача состоит в том, чтобы распознать многочисленные компоненты волны Лэмба в полученной форме сигнала и интерпретировать их с точки зрения движения источника. Это контрастирует с ситуацией в ультразвуковом контроле, где первой задачей является создание одной, хорошо контролируемой моды волны Лэмба на одной частоте. Но даже при ультразвуковом контроле преобразование мод происходит, когда генерируемая волна Лэмба взаимодействует с дефектами, поэтому интерпретация отраженных сигналов, составленных из нескольких мод, становится средством определения характеристик дефектов.

См. также

• Акустика
• Акустическая волна
• Волновое уравнение
• Волновод
• Волновод (акустика)
• Волновод (электромагнетизм)

Ссылки

• Роуз, JL; «Ультразвуковые волны в твердых средах», издательство Кембриджского университета, 1999.

Внешние ссылки

• Способы распространения звуковых волн в Ресурсном центре NDT
• Волна Лэмба в Энциклопедии неразрушающего контроля
• Волновой анализ Лэмба акусто-ультразвуковых сигналов в пластине Лю Чжэньцин: статья, которая включает полные волновые уравнения Лэмба.