Остановка времени

Пример времени остановки: момент достижения броуновского движения . Процесс начинается с 0 и останавливается, как только достигает 1.

В теории вероятностей , в частности при изучении случайных процессов , время остановки (также время Маркова , момент Маркова , необязательное время остановки или необязательное время ^[1]) — это особый тип «случайного времени»: случайная величина , значение которой интерпретируется как время, в которое данный случайный процесс демонстрирует определенное интересующее поведение. Время остановки часто определяется правилом остановки — механизмом принятия решения о продолжении или остановке процесса на основе текущего положения и прошлых событий, которое почти всегда приводит к решению об остановке в какой-то конечный момент времени.

Время остановки возникает в теории принятия решений , и необязательная теорема об остановке является важным результатом в этом контексте. Остановка времени также часто применяется в математических доказательствах, чтобы «укротить континуум времени», как выразился Чанг в своей книге (1982).

Определение

Дискретное время

Позволять $\tau$ быть случайной величиной, которая определена в отфильтрованном вероятностном пространстве $(\Omega ,{\mathcal {F}},({\mathcal {F}}_{n})_{n\in \mathbb {N} },P)$ со значениями в $\mathbb {N} \cup \{+\infty \}$ . Затем $\tau$ называется временем остановки (по отношению к фильтрации $\mathbb {F} =(({\mathcal {F}}_{n})_{n\in \mathbb {N} }$ ), если выполнено следующее условие:

\{\tau =n\}\in {\mathcal {F}}_{n}

для всех

n

Интуитивно это условие означает, что «решение» о том, стоит ли вовремя остановиться, $n$ должны основываться только на имеющейся в данный момент информации $n$ , а не о какой-либо будущей информации.

Общий случай

Позволять $\tau$ быть случайной величиной, которая определена в отфильтрованном вероятностном пространстве $(\Omega ,{\mathcal {F}},({\mathcal {F}}_{t})_{t\in T},P)$ со значениями в $T$ . В большинстве случаев $T=[0,+\infty )$ . Затем $\tau$ называется временем остановки (по отношению к фильтрации $\mathbb {F} =({\mathcal {F}}_{t})_{t\in T}$ ), если выполнено следующее условие:

\{\tau \leq t\}\in {\mathcal {F}}_{t}

для всех

t\in T

Как адаптированный процесс

Позволять $\tau$ быть случайной величиной, которая определена в отфильтрованном вероятностном пространстве $(\Omega ,{\mathcal {F}},({\mathcal {F}}_{t})_{t\in T},P)$ со значениями в $T$ . Затем $\tau$ называется временем остановки, если случайный процесс $X=(X_{t})_{t\in T}$ , определяемый

X_{t}:={\begin{cases}1&{\text{ if }}t<\tau \\0&{\text{ if }}t\geq \tau \end{cases}}

адаптирован к фильтрации $\mathbb {F} =({\mathcal {F}}_{t})_{t\in T}$

Примеры

Чтобы проиллюстрировать некоторые примеры случайных моментов времени, когда правила отменяются, а некоторые нет, представьте себе игрока, играющего в рулетку с типичным преимуществом казино, начиная со 100 долларов и делая ставку 1 доллар на красное в каждой игре:

Сыграть ровно пять игр соответствует времени остановки τ = 5 и является правилом остановки.
Играть до тех пор, пока у них не кончатся деньги или пока они не сыграют 500 игр, является останавливающим правилом.
Игра до тех пор, пока они не наберут максимальную сумму, которую они когда-либо получат, не является правилом остановки и не предусматривает времени остановки, поскольку для этого требуется информация о будущем, а также о настоящем и прошлом.
Игра до тех пор, пока они не удвоят свои деньги (заимствование при необходимости) не является останавливающим правилом, поскольку существует положительная вероятность того, что они никогда не удвоят свои деньги. ^{[ нужны разъяснения (см. обсуждение ) ]}
Игра до тех пор, пока они не удвоят свои деньги или не закончатся, является правилом остановки, хотя потенциально нет ограничений на количество игр, в которые они играют, поскольку вероятность того, что они остановятся за конечное время, равна 1.

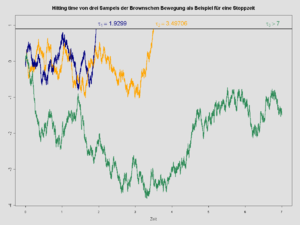
Чтобы проиллюстрировать более общее определение времени остановки, рассмотрим броуновское движение , которое является случайным процессом. $(B_{t})_{t\geq 0}$ , где каждый $B_{t}$ - случайная величина, определенная в вероятностном пространстве $(\Omega ,{\mathcal {F}},\mathbb {P} )$ . Мы определим фильтрацию в этом вероятностном пространстве, полагая ${\mathcal {F}}_{t}$ — σ -алгебра, порожденная всеми множествами вида $(B_{s})^{-1}(A)$ где $0\leq s\leq t$ и $A\subseteq \mathbb {R}$ является борелевским множеством . Интуитивно, событие E находится в ${\mathcal {F}}_{t}$ тогда и только тогда, когда мы можем определить, является ли E истинным или ложным, просто наблюдая за броуновским движением от момента времени 0 до момента времени t .

Каждая константа $\tau :=t_{0}$ (тривиально) время остановки; это соответствует правилу остановки «остановиться вовремя» $t_{0}$ ".
Позволять $a\in \mathbb {R} .$ Затем $\tau :=\inf\{t\geq 0\mid B_{t}=a\}$ — время остановки броуновского движения, соответствующее правилу остановки: «остановиться, как только броуновское движение достигнет значения a ».
Другое время остановки определяется выражением $\tau :=\inf\{t\geq 1\mid B_{s}>0{\text{ for all }}s\in [t-1,t]\}$ . Это соответствует правилу остановки «остановиться, как только броуновское движение станет положительным на непрерывном участке длиной в 1 единицу времени».
В общем случае, если τ ₁ и τ ₂ — моменты остановки на $\left(\Omega ,{\mathcal {F}},\left\{{\mathcal {F}}_{t}\right\}_{t\geq 0},\mathbb {P} \right)$ тогда их минимум $\tau _{1}\wedge \tau _{2}$ , их максимум $\tau _{1}\vee \tau _{2}$ , и их сумма τ ₁ + τ ₂ также являются моментами остановки. (Это не относится к различиям и продуктам, поскольку они могут потребовать «заглянуть в будущее», чтобы определить, когда остановиться.)

Время удара, подобное второму примеру выше, может быть важным примером времени остановки. Хотя сравнительно легко показать, что по существу все моменты остановки являются моментами попадания, ^[2] гораздо сложнее показать, что определенное время удара является временем остановки. Результаты последнего типа известны как теорема Дебю .

Локализация

Время остановки часто используется для обобщения определенных свойств случайных процессов на ситуации, в которых требуемое свойство удовлетворяется только в локальном смысле. Во-первых, если X — процесс и τ — время остановки, то X ^т используется для обозначения процесса X, остановленного в момент времени τ .

X_{t}^{\tau }=X_{\min(t,\tau )}

Тогда X говорят, что локально удовлетворяет некоторому свойству P, если существует последовательность моментов остановки τ _n , которая возрастает до бесконечности и для которой процессы

\mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}

удовлетворять P. свойству Общие примеры с набором индексов времени I = [0, ∞) следующие:

Локальный мартингальный процесс . Процесс X является локальным мартингалом, если он является càdlàg. ^{[ нужны разъяснения ]} и существует возрастающая до бесконечности последовательность моментов остановки τ _n такая, что
$\mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}$
является мартингалом для каждого n .

Локально интегрируемый процесс . Неотрицательный и возрастающий процесс X локально интегрируем, если существует последовательность моментов остановки τ _n, возрастающая до бесконечности, такая, что
$\operatorname {E} \left[\mathbf {1} _{\{\tau _{n}>0\}}X^{\tau _{n}}\right]<\infty$
для каждого н .

Виды времени остановки

Времена остановки с набором временных индексов I = [0,∞) часто делятся на один из нескольких типов в зависимости от того, можно ли предсказать, когда они вот-вот произойдут.

Время остановки τ является предсказуемым, если оно равно пределу возрастающей последовательности моментов остановки τ _n, удовлетворяющей τ _n < τ всякий раз, когда τ последовательность τ _n > 0. Говорят, что объявляет τ , и предсказуемые времена остановки иногда называют объявляемый .Примерами предсказуемого времени остановки являются времена начала непрерывных и адаптированных процессов. Если τ — это первый момент времени, когда непрерывный и вещественнозначный процесс X равен некоторому значению a , то это объявляется последовательностью τ _n , где τ _n — первый момент времени, когда X находится на расстоянии 1/ n из а .

Доступное время остановки – это время, которое можно охватить последовательностью предсказуемых времен. То есть момент остановки τ доступен, если P( τ = τ _n для некоторого n ) = 1, где τ _n — предсказуемые моменты времени.

Время остановки τ совершенно недоступно , если оно никогда не может быть объявлено возрастающей последовательностью моментов остановки. Эквивалентно, P( τ = σ < ∞) = 0 для каждого прогнозируемого времени σ . Примеры совершенно недоступных моментов остановки включают времена скачка пуассоновских процессов .

Каждое время остановки τ можно однозначно разложить на доступное и совершенно недоступное время. То есть существует единственное доступное время остановки σ и полностью недоступное время υ такие, что τ = σ всякий раз, когда σ < ∞, τ = υ всякий раз, когда υ < ∞, и τ = ∞ всякий раз, когда σ = υ = ∞. Обратите внимание, что в формулировке этого результата разложения время остановки не обязательно должно быть почти наверняка конечным и может равняться ∞.

Правила остановки в клинических исследованиях

Клинические испытания в медицине часто проводят промежуточный анализ, чтобы определить, достигло ли исследование уже своих конечных точек.Однако промежуточный анализ создает риск ложноположительных результатов, поэтому границы остановки используются для определения количества и времени промежуточного анализа (также известного как альфа-расходы, чтобы обозначить уровень ложноположительных результатов).В каждом из промежуточных тестов R испытание прекращается, если вероятность оказывается ниже порога p, который зависит от используемого метода. См. Последовательный анализ .

См. также

Ссылки

^ Калленберг, Олав (2017). Случайные меры, теория и приложения . Теория вероятностей и стохастическое моделирование. Том. 77. Швейцария: Шпрингер. п. 347. дои : 10.1007/978-3-319-41598-7 . ISBN 978-3-319-41596-3 .
^ Фишер, Том (2013). «О простых представлениях времен остановки и сигма-алгебр времени остановки». Статистика и вероятностные буквы . 83 (1): 345–349. arXiv : 1112.1603 . дои : 10.1016/j.spl.2012.09.024 .

Дальнейшее чтение

Томас С. Фергюсон , «Кто решил проблему секретаря?», Стат. наук. том. 4, 282–296 (1989).
Введение в остановку времени.
Ф. Томас Брюсс , «Суммируйте шансы до единицы и остановитесь», Annals of Probability, Vol. 4, 1384–1391, (2000)
Чанг, Кай Лай (1982). Лекции от марковских процессов до броуновского движения . Основные учения математических наук №1. 249. Нью-Йорк, штат Нью-Йорк: Springer Verlag. ISBN 978-0-387-90618-8 .
Х. Винсент Пур и Олимпия Хаджилиадис (2008). Самое быстрое обнаружение (Первое изд.). Кембридж, Англия: Издательство Кембриджского университета. ISBN 978-0-521-62104-5 .
Проттер, Филип Э. (2005). Стохастическое интегрирование и дифференциальные уравнения . Стохастическое моделирование и прикладная теория вероятности № 21 (2-е издание (версия 2.1, исправленное 3-е издание) изд.). Берлин: Springer-Verlag. ISBN 978-3-540-00313-7 .
Ширяев, Альберт Н. (2007). Правила оптимальной остановки . Спрингер. ISBN 978-3-540-74010-0 .

[1] Калленберг, Олав (2017). Случайные меры, теория и приложения . Теория вероятностей и стохастическое моделирование. Том. 77. Швейцария: Шпрингер. п. 347. дои : 10.1007/978-3-319-41598-7 . ISBN 978-3-319-41596-3 .

[Fischer_(2013)-2] Фишер, Том (2013). «О простых представлениях времен остановки и сигма-алгебр времени остановки». Статистика и вероятностные буквы . 83 (1): 345–349. arXiv : 1112.1603 . дои : 10.1016/j.spl.2012.09.024 .

[1]

[2]