Расширенный стандарт шифрования

Расширенный стандарт шифрования
(Рейндал)

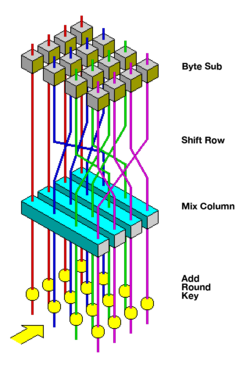Визуализация функции раунда AES
Общий
Дизайнеры	Джоан Дэмен , Винсент Раймен
Впервые опубликовано	1998
Получено из	Квадрат
Преемники	Anubis , Grand Cru , Kalyna
Сертификация	Победитель AES , CRYPTREC , NESSIE , АНБ
Деталь шифрования
Размеры ключей	128, 192 или 256 бит
Размеры блоков	128 бит
Структура	Сеть замены-перестановки
Раунды	10, 12 или 14 (в зависимости от размера ключа)
Лучший публичный криптоанализ
Были опубликованы атаки, которые в вычислительном отношении быстрее, чем полная атака методом перебора , хотя по состоянию на 2023 год ни одна из них не является вычислительно осуществимой. Для AES-128 ключ можно восстановить с вычислительной сложностью 2 126.1 используя бикличную атаку . Для бикличных атак на AES-192 и AES-256 вычислительная сложность 2 189.7 и 2 254.4 соответственно применять. Атаки с использованием связанных ключей могут сломать AES-256 и AES-192 со сложностью 2. 99.5 и 2 176 как по времени, так и по данным соответственно. Еще одна атака была опубликована в блоге и выпущен в виде препринта в 2009 году. Эта атака направлена ​​на AES-256, который использует только два связанных ключа и 2 39 время для восстановления полного 256-битного ключа 9-раундовой версии или 2 45 время для версии из 10 раундов с более сильным типом атаки по соответствующему подразделу или 2 70 время для 11-раундовой версии.

Расширенный стандарт шифрования ( AES ), также известный под своим первоначальным названием Rijndael ( Голландское произношение: [ˈrɛindaːl] ), — это спецификация шифрования электронных данных, установленная Национальным институтом стандартов и технологий США (NIST) в 2001 году.

AES — это вариант блочного шифра Рейндала. разработанный двумя бельгийскими криптографами, Джоан Демен и Винсентом Рейменом , которые представили предложение в NIST во время процесса выбора AES . Rijndael — это семейство шифров с разными размерами ключей и блоков. Для AES NIST выбрал трех членов семейства Rijndael, каждый из которых имеет размер блока 128 бит, но три разные длины ключей: 128, 192 и 256 бит.

AES был принят правительством США . Он заменяет стандарт шифрования данных (DES). который был опубликован в 1977 году. Алгоритм, описанный AES, представляет собой алгоритм с симметричным ключом , то есть один и тот же ключ используется как для шифрования, так и для дешифрования данных.

В США NIST объявил AES как US FIPS PUB 197 (FIPS 197). 26 ноября 2001 года Это объявление последовало за пятилетним процессом стандартизации, в ходе которого были представлены и оценены пятнадцать конкурирующих проектов, прежде чем шифр Рейндала был выбран как наиболее подходящий.

AES включен в стандарт ISO / IEC 18033-3 . AES вступил в силу в качестве стандарта федерального правительства США 26 мая 2002 года после одобрения министром торговли США Дональдом Эвансом . AES доступен во многих различных пакетах шифрования и является первым (и единственным) общедоступным шифром, одобренным Агентством национальной безопасности США (АНБ) для сверхсекретной информации при использовании в криптографическом модуле, одобренном АНБ.

Окончательные стандарты

Стандарт расширенного шифрования (AES) определен в каждом из:

• FIPS PUB 197: Стандарт расширенного шифрования (AES).
• ISO/IEC 18033-3: Блочные шифры.

Описание шифров

AES основан на принципе проектирования, известном как сеть замены-перестановки , и эффективен как в программном, так и в аппаратном обеспечении. В отличие от своего предшественника DES, AES не использует сеть Фейстеля . AES — это вариант Rijndael с фиксированным размером блока 128 бит и размером ключа 128, 192 или 256 бит. Напротив, Rijndael как таковой определяется размерами блоков и ключей, которые могут быть кратны 32 битам, минимум 128 и максимум 256 бит. Большинство вычислений AES выполняются в определенном конечном поле .

AES работает с массивом 4 × 4 по столбцам размером 16 байт b ₀ ,   b ₁ ,   ...,   b _15, называемым состоянием :

${\begin{bmatrix}b_{0}&b_{4}&b_{8}&b_{12}\\b_{1}&b_{5}&b_{9}&b_{13}\\b_{2}&b_{6}&b_{10}&b_{14}\\b_{3}&b_{7}&b_{11}&b_{15}\end{bmatrix}}$

Размер ключа, используемый для шифрования AES, определяет количество раундов преобразования, которые преобразуют входные данные, называемые открытым текстом , в конечный результат, называемый зашифрованным текстом . Количество раундов следующее:

• 10 раундов для 128-битных ключей.
• 12 раундов для 192-битных ключей.
• 14 раундов для 256-битных ключей.

Каждый раунд состоит из нескольких этапов обработки, в том числе одного, который зависит от самого ключа шифрования. Для преобразования зашифрованного текста обратно в исходный открытый текст применяется набор обратных раундов с использованием того же ключа шифрования.

Общее описание алгоритма

1. KeyExpansion — раундовые ключи извлекаются из ключа шифрования с использованием расписания ключей AES . Для AES требуется отдельный 128-битный блок ключей раунда для каждого раунда плюс еще один.
2. Добавление ключа начального раунда:
   1. AddRoundKey — каждый байт состояния объединяется с байтом раундового ключа с помощью побитового xor .
3. 9, 11 или 13 раундов:
   1. SubBytes — шаг нелинейной замены, при котором каждый байт заменяется другим в соответствии с справочной таблицей .
   2. ShiftRows — шаг транспонирования, при котором последние три строки состояния циклически сдвигаются на определенное количество шагов.
   3. MixColumns — операция линейного смешивания, которая работает со столбцами состояния, объединяя четыре байта в каждом столбце.
   4. Аддраундкей
4. Финальный раунд (всего 10, 12 или 14 раундов):
   1. Суббайты
   2. ShiftRows
   3. Аддраундкей

The суббайтов Шаг

Основная статья: Rijndael S-box

В Шаг SubBytes , каждый байт в состоянии заменяется его записью в фиксированной 8-битной таблице поиска S ; б _{ij знак} равно S(а _ij ) .

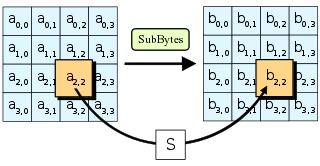
В Шаг SubBytes , каждый байт $a_{i,j}$ в массиве состояний заменяется на суббайт $S(a_{i,j})$ с использованием 8-битного поля подстановки . До раунда 0 массив состояний представляет собой просто открытый текст/вход. Эта операция обеспечивает нелинейность шифра . Используемый S-блок получен из мультипликативной обратной операции по GF (2 ⁸ ) , как известно, обладает хорошими нелинейными свойствами. Чтобы избежать атак, основанных на простых алгебраических свойствах, S-блок строится путем объединения обратной функции с обратимым аффинным преобразованием . S-блок также выбран для того, чтобы избежать каких-либо фиксированных точек (и, следовательно, расстройства ), т. е. $S(a_{i,j})\neq a_{i,j}$, а также любые противоположные неподвижные точки, т. е. $S(a_{i,j})\oplus a_{i,j}\neq {\text{FF}}_{16}$. При выполнении расшифровки Шаг InvSubBytes (обратный шагу SubBytes ), для чего необходимо сначала взять обратное аффинное преобразование, а затем найти мультипликативное обратное преобразование.

The ShiftRows Шаг

В Шаг ShiftRows , байты в каждой строке состояния циклически сдвигаются влево. Количество мест, на которые сдвигается каждый байт, постепенно различается для каждой строки.

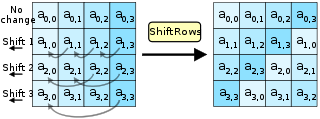
The Шаг ShiftRows работает со строками состояния; он циклически сдвигает байты в каждой строке на определенное смещение . Для AES первая строка остается неизменной. Каждый байт второй строки сдвигается на единицу влево. Аналогичным образом третья и четвертая строки сдвигаются на два и три соответственно. Таким образом, каждый столбец выходного состояния Шаг ShiftRows состоит из байтов из каждого столбца входного состояния. Важность этого шага состоит в том, чтобы избежать независимого шифрования столбцов, и в этом случае AES выродится в четыре независимых блочных шифра.

The MixColumns Шаг

Основная статья: Rijndael MixColumns

В Шаг MixColumns , каждый столбец состояния умножается на фиксированный полином. $c(x)$.

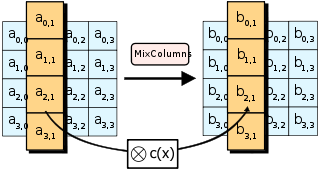
В На этапе MixColumns четыре байта каждого столбца состояния объединяются с помощью обратимого линейного преобразования . Функция MixColumns принимает четыре байта на вход и выводит четыре байта, причем каждый входной байт влияет на все четыре выходных байта. Вместе с ShiftRows , MixColumns обеспечивает диффузию в шифре.

Во время этой операции каждый столбец преобразуется с использованием фиксированной матрицы (матрица, умноженная слева на столбец, дает новое значение столбца в состоянии):

${\begin{bmatrix}b_{0,j}\\b_{1,j}\\b_{2,j}\\b_{3,j}\end{bmatrix}}={\begin{bmatrix}2&3&1&1\\1&2&3&1\\1&1&2&3\\3&1&1&2\end{bmatrix}}{\begin{bmatrix}a_{0,j}\\a_{1,j}\\a_{2,j}\\a_{3,j}\end{bmatrix}}\qquad 0\leq j\leq 3$

Умножение матрицы состоит из умножения и сложения элементов. Записи представляют собой байты, рассматриваемые как коэффициенты полинома порядка $x^{7}$. Сложение — это просто XOR. Умножение является неприводимым по модулю многочленом. $x^{8}+x^{4}+x^{3}+x+1$. Если обработка побитовая, то после сдвига должно выполняться условное исключающее ИЛИ с 1B ₁₆ , если сдвинутое значение больше FF ₁₆ (переполнение необходимо исправить вычитанием порождающего полинома). Это частные случаи обычного умножения в $\operatorname {GF} (2^{8})$.

В более общем смысле каждый столбец рассматривается как полином по $\operatorname {GF} (2^{8})$ и затем умножается по модулю ${01}_{16}\cdot z^{4}+{01}_{16}$ с фиксированным полиномом $c(z)={03}_{16}\cdot z^{3}+{01}_{16}\cdot z^{2}+{01}_{16}\cdot z+{02}_{16}$. Коэффициенты отображаются в шестнадцатеричном эквиваленте двоичного представления битовых полиномов из $\operatorname {GF} (2)[x]$. Шаг MixColumns также можно рассматривать как умножение на показанную конкретную матрицу MDS в конечном поле. $\operatorname {GF} (2^{8})$. Подробнее этот процесс описан в статье Rijndael MixColumns .

The Аддраундкей

В На этапе AddRoundKey каждый байт состояния объединяется с байтом раундового подключа с помощью операции XOR (⊕).

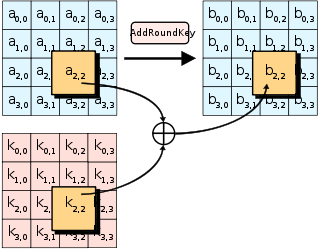
В AddRoundKey , подраздел объединяется с состоянием. получается дополнительный ключ Для каждого раунда из основного ключа с использованием расписания ключей Рейндала ; каждый подраздел имеет тот же размер, что и состояние. Подключ добавляется путем объединения состояния с соответствующим байтом подраздела с помощью побитового XOR .

Оптимизация шифра

В системах с 32-битными словами и более можно ускорить выполнение этого шифра, объединив Суббайты и ShiftRows выполняет действия с MixColumns преобразует их в последовательность поиска в таблице. Для этого требуются четыре 32-битные таблицы по 256 записей (вместе занимающие 4096 байт). Затем раунд может быть выполнен с 16 операциями поиска по таблице и 12 32-битными операциями «исключающее ИЛИ», за которыми следуют четыре 32-битные операции «исключающее ИЛИ» в Шаг AddRoundKey . Альтернативно, операция поиска в таблице может выполняться с одной 32-битной таблицей с 256 элементами (занимающей 1024 байта), за которой следуют операции кругового вращения.

Используя байт-ориентированный подход, можно объединить Суббайты , ShiftRows и MixColumns выполняет одну операцию раунда.

Безопасность

Агентство национальной безопасности (АНБ) проверило всех финалистов AES, включая Рейндала, и заявило, что все они достаточно безопасны для несекретных данных правительства США. В июне 2003 года правительство США объявило, что AES может использоваться для защиты секретной информации :

Конструкция и надежность всех длин ключей алгоритма AES (т. е. 128, 192 и 256) достаточны для защиты секретной информации до уровня СЕКРЕТНО. СОВЕРШЕННО СЕКРЕТНАЯ информация потребует использования ключей длиной 192 или 256. Внедрение AES в продукты, предназначенные для защиты систем и/или информации национальной безопасности, должно быть проверено и сертифицировано АНБ до их приобретения и использования.

AES имеет 10 раундов для 128-битных ключей, 12 раундов для 192-битных ключей и 14 раундов для 256-битных ключей.

К 2006 году самые известные атаки включали 7 раундов для 128-битных ключей, 8 раундов для 192-битных ключей и 9 раундов для 256-битных ключей.

Известные атаки

Для криптографов криптографический «взлом» — это нечто более быстрое, чем атака методом перебора ,    т. е. последовательное выполнение одной пробной расшифровки для каждого возможного ключа. (см. Криптоанализ § Требуемые вычислительные ресурсы ) . Таким образом, перерыв может привести к результатам, недостижимым при нынешних технологиях. Несмотря на свою непрактичность, теоретические прорывы иногда могут дать представление о закономерностях уязвимости. Самая крупная успешная общеизвестная брутфорс-атака на широко распространенный алгоритм блочного шифрования была проведена RC5 против 64-битного ключа распределенным.net в 2006 году.

Ключевое пространство увеличивается в 2 раза для каждого дополнительного бита длины ключа, и если каждое возможное значение ключа равновероятно; это приводит к удвоению среднего времени поиска ключа методом перебора с каждым дополнительным битом длины ключа. Это означает, что усилия по перебору растут экспоненциально с увеличением длины ключа. Длина ключа сама по себе не подразумевает защиту от атак, поскольку существуют шифры с очень длинными ключами, которые оказались уязвимыми.

AES имеет довольно простую алгебраическую структуру. о теоретической атаке, получившей название « XSL-атака объявили В 2002 году Николя Куртуа и Йозеф Пепшик », которая якобы продемонстрировала слабость алгоритма AES, частично из-за низкой сложности его нелинейных компонентов. С тех пор другие документы показали, что атака в первоначальном виде неработоспособна; см. XSL-атаку на блочные шифры .

В процессе выбора AES разработчики конкурирующих алгоритмов написали об алгоритме Рейндала: «Мы обеспокоены его использованием… в приложениях, критически важных для безопасности». Однако в октябре 2000 года, в конце процесса отбора AES, Брюс Шнайер , разработчик конкурирующего алгоритма Twofish , написал, что, хотя он и думал, что когда-нибудь будут разработаны успешные академические атаки на Рейндал, он «не верил, что кто-нибудь когда-нибудь сможет это сделать». обнаружить атаку, которая позволит кому-то читать трафик Rijndael».

До мая 2009 года единственными успешными опубликованными атаками на полную версию AES были атаки по побочным каналам на некоторые конкретные реализации. В 2009 году была обнаружена новая атака с использованием связанных ключей , которая использует простоту расписания ключей AES и имеет сложность 2. ¹¹⁹ . В декабре 2009 года он был улучшен до 2. ^99.5 . Это продолжение атаки, обнаруженной ранее в 2009 году Алексом Бирюковым , Дмитрием Ховратовичем и Ивицей Николичем, сложностью 2. ⁹⁶ для одного из каждых 2 ³⁵ ключи. Однако атаки с использованием связанных ключей не вызывают беспокойства в любом правильно спроектированном криптографическом протоколе, поскольку правильно разработанный протокол (т. е. реализующее программное обеспечение) позаботится о том, чтобы не допустить использования связанных ключей, по существу, ограничивая средства злоумышленника по выбору ключей для определения связанности.

Еще одну атаку опубликовал в блоге Брюс Шнайер. 30 июля 2009 г. и выпущен в виде препринта. 3 августа 2009 года. Эта новая атака, осуществленная Алексом Бирюковым, Орром Данкельманом , Натаном Келлером , Дмитрием Ховратовичем и Ади Шамиром , направлена ​​против AES-256, который использует только два связанных ключа и 2 ³⁹ время для восстановления полного 256-битного ключа 9-раундовой версии или 2 ⁴⁵ время для версии из 10 раундов с более сильным типом атаки по соответствующему подразделу или 2 ⁷⁰ время для 11-раундовой версии. 256-битный AES использует 14 раундов, поэтому эти атаки не эффективны против полного AES.

Практичность этих атак с использованием более сильных связанных ключей подверглась критике. например, в статье об атаках с выбранными ключевыми отношениями посередине на AES-128, написанной Винсентом Рейменом в 2010 году.

В ноябре 2009 года в виде препринта была выпущена первая атака с известным ключом против сокращенной 8-раундовой версии AES-128. Эта атака с распознаванием известного ключа представляет собой усовершенствованную атаку, или атаку «начало с середины», против AES-подобных перестановок, которые рассматривают два последовательных раунда перестановки как применение так называемого Super-S-box. . Работает на 8-раундовой версии AES-128 с временной сложностью 2 ⁴⁸ и сложность памяти 2 ³² . 128-битный AES использует 10 раундов, поэтому эта атака не эффективна против полного AES-128.

Первые атаки с восстановлением ключей на полный AES были осуществлены Андреем Богдановым, Дмитрием Ховратовичем и Кристианом Рехбергером и были опубликованы в 2011 году. Атака представляет собой бикликовую атаку , которая быстрее грубой силы примерно в четыре раза. Требуется 2 ^126.2 операции по восстановлению ключа AES-128. Для AES-192 и AES-256, 2 ^190.2 и 2 ^254.6 соответственно необходимы операции. Этот результат был дополнительно улучшен до 2 ^126.0 для АЭС-128, 2 ^189.9 для АЭС-192 и 2 ^254.3 для АЭС-256, это лучшие на данный момент результаты в атаке с восстановлением ключа против AES.

Это очень небольшой выигрыш, поскольку для подбора 126-битного ключа (вместо 128 бит) все равно потребуются миллиарды лет на нынешнем и прогнозируемом оборудовании. Также авторы рассчитывают лучшую атаку по своей методике на AES со 128-битным ключом, требующим хранения 2 ⁸⁸ биты данных. Это около 38 триллионов терабайт данных, что больше, чем все данные, хранящиеся на всех компьютерах планеты в 2016 году. В статье 2015 года пространственная сложность была повышена до 2. ⁵⁶ биты, что составляет 9007 терабайт (при сохранении временной сложности 2 ^126.2 ).

Согласно документам Сноудена , АНБ проводит исследование того, может ли криптографическая атака, основанная на статистике тау, помочь взломать AES.

В настоящее время не известна практическая атака, которая позволила бы кому-то, не зная ключа, прочитать данные, зашифрованные с помощью AES, при правильной реализации.

Атаки по побочным каналам

Атаки по побочным каналам не атакуют шифр как « черный ящик» и, следовательно, не связаны с безопасностью шифра, как это определено в классическом контексте, но важны на практике. Они атакуют реализации шифра на аппаратных или программных системах, которые непреднамеренно сливают данные. Известно несколько таких атак на различные реализации AES.

В апреле 2005 года DJ Бернштейн объявил об атаке с использованием синхронизации кэша, которую он использовал для взлома пользовательского сервера, использующего OpenSSL . шифрование AES Для атаки потребовалось более 200 миллионов выбранных открытых текстов. Пользовательский сервер был спроектирован так, чтобы выдавать как можно больше информации о времени (сервер сообщает о количестве машинных циклов, затраченных на операцию шифрования). Однако, как отметил Бернштейн, «уменьшение точности временных меток сервера или исключение их из ответов сервера не останавливает атаку: клиент просто использует время туда и обратно на основе своих локальных часов и компенсирует повышенный шум». путем усреднения по большему количеству образцов».

В октябре 2005 года Даг Арне Освик, Ади Шамир и Эран Тромер представили документ, демонстрирующий несколько атак с использованием тайминга кэша против реализаций AES, обнаруженных в OpenSSL и Linux. dm-crypt функция шифрования раздела. Одна атака смогла получить весь ключ AES всего после 800 операций, запускающих шифрование, в общей сложности за 65 миллисекунд. Эта атака требует, чтобы злоумышленник имел возможность запускать программы в той же системе или платформе, на которой используется AES.

В декабре 2009 года была опубликована атака на некоторые аппаратные реализации, которая использовала дифференциальный анализ ошибок и позволяла восстановить ключ со сложностью 2. ³² .

В ноябре 2010 года Эндре Бангертер, Дэвид Галлаш и Стефан Кренн опубликовали статью, в которой описывался практический подход к восстановлению секретных ключей из AES-128 «почти в реальном времени» без необходимости использования зашифрованного или открытого текста. Этот подход также работает в реализациях AES-128, использующих таблицы сжатия, таких как OpenSSL. Как и некоторые более ранние атаки, эта требует возможности запуска непривилегированного кода в системе, выполняющего шифрование AES, что может быть достигнуто путем заражения вредоносным ПО гораздо проще, чем захват учетной записи root.

В марте 2016 года Ашоккумар К., Рави Пракаш Гири и Бернард Менезес представили атаку по побочному каналу на реализации AES, которая может восстановить полный 128-битный ключ AES всего за 6–7 блоков открытого/зашифрованного текста, что является существенным улучшением по сравнению с предыдущие работы, требующие от 100 до миллиона шифрований. Предлагаемая атака требует стандартных привилегий пользователя и алгоритмов получения ключей, которые выполняются менее чем за минуту.

Многие современные процессоры имеют встроенные аппаратные инструкции для AES , которые защищают от атак по побочным каналам, связанных с синхронизацией.

Квантовые атаки

AES-256 считается квантовоустойчивым , поскольку он имеет квантовую устойчивость, аналогичную устойчивости AES-128 к традиционным, неквантовым атакам при уровне безопасности 128 бит . AES-192 и AES-128 не считаются квантовоустойчивыми из-за меньшего размера ключей. Устойчивость AES-192 к квантовым атакам составляет 96 бит, а устойчивость AES-128 к квантовым атакам составляет 64 бита, что делает их оба небезопасными.

Проверка NIST/CSEC

Программа проверки криптографических модулей (NIST) правительства США Национального института стандартов и технологий (CMVP) осуществляется совместно Отделом компьютерной безопасности и Управлением безопасности связи (CSE) правительства Канады. использования криптографических модулей, соответствующих стандарту NIST FIPS 140-2, Правительство США требует для шифрования всех данных, имеющих класс конфиденциальности, но неклассифицированный (SBU) или выше. Из NSTISSP № 11, Национальная политика, регулирующая получение информации: «Продукты шифрования для защиты секретной информации будут сертифицированы АНБ, а продукты шифрования, предназначенные для защиты конфиденциальной информации, будут сертифицированы в соответствии с NIST FIPS 140-2».

Правительство Канады также рекомендует использовать криптографические модули, проверенные по стандарту FIPS 140, в несекретных приложениях своих ведомств.

Хотя публикация NIST 197 («FIPS 197») является уникальным документом, охватывающим алгоритм AES, поставщики обычно обращаются к CMVP в соответствии с FIPS 140 и просят проверить несколько алгоритмов (например, Triple DES или SHA1 ) одновременно. Таким образом, редко можно найти криптографические модули, которые однозначно проверены на соответствие FIPS 197, а сам NIST обычно не тратит время на отдельный список модулей, проверенных на соответствие FIPS 197, на своем общедоступном веб-сайте. Вместо этого проверка FIPS 197 обычно указывается как обозначение «Одобрено FIPS: AES» (с конкретным номером сертификата FIPS 197) в текущем списке проверенных криптографических модулей FIPS 140.

Программа проверки криптографических алгоритмов (CAVP) позволяет провести независимую проверку правильности реализации алгоритма AES. Успешная проверка приводит к включению в список на странице проверок NIST. Это тестирование является обязательным условием для проверки модуля FIPS 140-2. Однако успешная проверка CAVP никоим образом не означает, что криптографический модуль, реализующий алгоритм, безопасен. Криптографический модуль, не имеющий проверки FIPS 140-2 или специального одобрения АНБ, не считается безопасным правительством США и не может использоваться для защиты правительственных данных.

Пройти валидацию FIPS 140-2 сложно как с технической, так и с финансовой точки зрения. Существует стандартизированный набор тестов, а также элемент проверки исходного кода, который необходимо пройти в течение нескольких недель. Стоимость проведения этих тестов в утвержденной лаборатории может быть значительной (например, более 30 000 долларов США). и не включает время, необходимое для написания, тестирования, документирования и подготовки модуля к валидации. После проверки модули должны быть повторно отправлены и повторно оценены, если они каким-либо образом были изменены. Это может варьироваться от простого обновления документации, если функциональность безопасности не изменилась, до более существенного набора повторных проверок, если изменение повлияло на функциональность безопасности.

Тестовые векторы

Тестовые векторы представляют собой набор известных шифров для данного ввода и ключа. NIST распространяет эталонные тестовые векторы AES как векторы теста известных ответов AES (KAT).

Производительность

Высокая скорость и низкие требования к оперативной памяти были одними из критериев процесса выбора AES. В качестве выбранного алгоритма AES хорошо зарекомендовал себя на широком спектре оборудования: от 8-битных смарт-карт до высокопроизводительных компьютеров.

На Pentium Pro шифрование AES требует 18 тактов на байт (cpb), эквивалентно пропускной способности около 11 МБ/с для процессора с частотой 200 МГц.

На процессорах Intel Core и AMD Ryzen, поддерживающих расширения набора инструкций AES-NI , пропускная способность может составлять несколько ГиБ/с. На процессоре Intel Westmere шифрование AES с использованием AES-NI занимает около 1,3 cpb для AES-128 и 1,8 cpb для AES-256.

Реализации

Основная статья: Реализации AES

См. также

• Режимы работы AES
• Шифрование диска
• Whirlpool — хэш-функция, созданная Винсентом Рейменом и Пауло С.Л.М. Баррето.
• Список бесплатных пакетов программного обеспечения с открытым исходным кодом

Ссылки

• Куртуа, Николя; Пепшик, Йозеф (2003). «Криптоанализ блочных шифров с переопределенными системами уравнений» . Ин Чжэн, Юлян (ред.). Достижения в криптологии – ASIACRYPT 2002: 8-я Международная конференция по теории и применению криптологии и информационной безопасности, Квинстаун, Новая Зеландия, 1–5 декабря 2002 г., Материалы . Спрингер. стр. 268–287. ISBN  978-3-540-36178-7 .
• Дэмен, Джоан; Раймс, Винсент (2002). Дизайн Rijndael: AES — расширенный стандарт шифрования . Спрингер. ISBN  978-3-540-42580-9 .
• Паар, Кристоф; Пельцль, Ян (2009). Понимание криптографии: Учебник для студентов и практиков . Спрингер. стр. 87–122. ISBN  978-3-642-04101-3 . альтернативная ссылка (сопутствующий веб-сайт содержит онлайн-лекции по AES)

Внешние ссылки

• «256-битный ключ – 128-битный блок – AES» . Криптография – 256-битные шифры: справочный исходный код и материалы для участия в международных конкурсах криптографических проектов . Встроенное ПО.
• «Расширенный стандарт шифрования (AES)» (PDF) . Федеральные стандарты обработки информации . 26 ноября 2001 г. doi : 10.6028/NIST.FIPS.197 . 197.
• Информация из архива алгоритма AES – (старая, неподдерживаемая)
• «Часть 3: Блочные шифры» (PDF) . Информационные технологии – Методы безопасности – Алгоритмы шифрования (2-е изд.). ИСО. 15 декабря 2010 г. ИСО/МЭК 18033-3:2010(Е). Архивировано (PDF) из оригинала 9 октября 2022 г.
• Анимация Рейндала – AES подробно объяснена и анимирована с использованием Flash (Энрике Забала / Университет ОРТ / Монтевидео / Уругвай). Эта анимация (на английском, испанском и немецком языках) также является частью CrypTool 1 (меню Индив. Процедуры → Визуализация алгоритмов → AES).
• HTML5-анимация Rijndael — та же анимация, что и выше, сделанная в HTML5.