Поиск в ширину

Поиск в ширину
	Order in which the nodes get expanded Порядок раскрытия узлов
Сорт	Алгоритм поиска
Структура данных	График
Худшая производительность
Наихудшая пространственная сложность
Оптимальный	да (для невзвешенных графиков)

Анимированный пример поиска в ширину. Черный: изучен, серый: поставлен в очередь для дальнейшего изучения.

Верхняя часть «Крестики-нолики» дерева игры

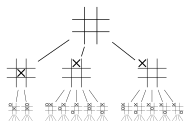
Поиск в ширину ( BFS ) — это алгоритм поиска в древовидной структуре данных узла, удовлетворяющего заданному свойству. Он начинается с корня дерева и исследует все узлы на текущей глубине, прежде чем перейти к узлам на следующем уровне глубины. Дополнительная память, обычно очередь , необходима для отслеживания дочерних узлов, которые были обнаружены, но еще не исследованы.

Например, в шахматном эндшпиле шахматный движок может построить дерево игры из текущей позиции, применяя все возможные ходы и используя поиск в ширину, чтобы найти выигрышную позицию для белых. Неявные деревья (например, игровые деревья или другие деревья решения задач) могут иметь бесконечный размер; поиск в ширину гарантированно найдет узел решения ^[1] если таковой существует.

Напротив, (простой) поиск в глубину (DFS), который исследует ветвь узла как можно дальше, прежде чем возвращаться и расширять другие узлы. ^[2] может заблудиться в бесконечной ветке и так и не добраться до узла решения. Итеративный поиск в глубину с углублением позволяет избежать последнего недостатка ценой повторного исследования верхних частей дерева. С другой стороны, оба алгоритма поиска в глубину обычно требуют гораздо меньше дополнительной памяти, чем поиск в ширину. ^[3]

Поиск в ширину можно обобщить как на неориентированные графы, так и на ориентированные графы с заданным начальным узлом (иногда называемым «ключом поиска»). ^[4] При поиске в пространстве состояний в искусственном интеллекте часто допускаются повторные поиски вершин, тогда как при теоретическом анализе алгоритмов, основанных на поиске в ширину, обычно принимаются меры предосторожности для предотвращения повторений.

BFS и ее применение для поиска компонентов связности графов были изобретены в 1945 году Конрадом Цузе в его (отвергнутой) докторской диссертации. диссертацию по языку программирования Plankalkül , но она не была опубликована до 1972 года. ^[5] Его заново изобрел в 1959 году Эдвард Ф. Мур , который использовал его, чтобы найти кратчайший путь из лабиринта. ^[6]^[7] и позже разработан С.А. Ли в алгоритм маршрутизации проводов (опубликован в 1961 г.). ^[8]

Псевдокод

Входные данные : граф $G$ и начальный $корень$ вершины $G.$

Выход : Целевое состояние. Родительские ссылки прослеживают кратчайший путь до $корня$ ^[9]

 1  procedure BFS(G, root) is
 2      let Q be a queue
 3      label root as explored
 4      Q.enqueue(root)
 5      while Q is not empty do
 6          v := Q.dequeue()
 7          if v is the goal then
 8              return v
 9          for all edges from v to w in G.adjacentEdges(v) do
10              if w is not labeled as explored then
11                  label w as explored
12                  w.parent := v
13                  Q.enqueue(w)

Подробнее

Эта нерекурсивная реализация аналогична нерекурсивной реализации поиска в глубину , но отличается от нее двумя способами:

он использует очередь ( First In First Out ) вместо стека ( Last In First Out ) и
он проверяет, была ли вершина исследована, прежде чем поставить вершину в очередь, вместо того, чтобы откладывать эту проверку до тех пор, пока вершина не будет исключена из очереди.

Если $G$ — дерево , замена очереди этого алгоритма поиска в ширину стеком даст алгоритм поиска в глубину. Для общих графов замена стека реализации итеративного поиска в глубину очередью также приведет к созданию алгоритма поиска в ширину, хотя и несколько нестандартного. ^[10]

Очередь Q содержит границу, вдоль которой алгоритм выполняет поиск.

Узлы можно пометить как исследованные, сохранив их в наборе или по атрибуту на каждом узле, в зависимости от реализации.

Обратите внимание, что слово node обычно взаимозаменяемо со словом vertex .

атрибут Родительский каждого узла полезен для доступа к узлам по кратчайшему пути, например, путем возврата от узла назначения к начальному узлу после запуска BFS и установки узлов-предшественников.

Поиск в ширину создает так называемое дерево в ширину . Вы можете увидеть, как выглядит дерево в ширину , в следующем примере.

Пример

Ниже приведен пример дерева в ширину, полученного путем запуска BFS в немецких городах, начиная с Франкфурта :

Дерево в ширину, полученное при запуске BFS на данной карте и начиная с Франкфурта.

Анализ

Временная и пространственная сложность

Временную сложность можно выразить как $O(|V|+|E|)$ , поскольку в худшем случае будет исследована каждая вершина и каждое ребро. $|V|$ количество вершин и $|E|$ — количество ребер в графе. Обратите внимание, что $O(|E|)$ может варьироваться между $O(1)$ и $O(|V|^{2})$ , в зависимости от того, насколько разрежен входной граф. ^[11]

Когда количество вершин в графе известно заранее и для определения того, какие вершины уже добавлены в очередь, используются дополнительные структуры данных, сложность пространства можно выразить как $O(|V|)$ , где $|V|$ это количество вершин. Это помимо помещения требуется для самого графа и может варьироваться в зависимости от представления графа, используемого реализацией алгоритма.

При работе с графами, которые слишком велики для явного хранения (или бесконечны), практичнее описывать сложность поиска в ширину разными терминами: найти узлы, находящиеся на расстоянии $d$ от начального узла (измеряется числом обходов ребер), BFS принимает $O (b д + 1)$ время и память, где $b$ — « коэффициент ветвления » графа (средняя исходящая степень). ^[12]^: 81

Полнота

При анализе алгоритмов входными данными для поиска в ширину считается конечный граф, представленный в виде списка смежности , матрицы смежности или аналогичного представления. Однако при применении методов обхода графа в искусственном интеллекте входные данные могут быть неявным представлением бесконечного графа. В этом контексте метод поиска описывается как полный, если он гарантированно находит целевое состояние, если оно существует. Поиск в ширину завершен, а поиск в глубину — нет. При применении к бесконечным графам, представленным неявно, поиск в ширину в конечном итоге найдет целевое состояние, но поиск в глубину может потеряться в частях графа, которые не имеют целевого состояния и никогда не возвращаются. ^[13]

Заказ БФС

Перечисление вершин графа называется BFS-упорядочением, если оно является возможным результатом применения BFS к этому графу.

Позволять $G=(V,E)$ быть графиком с $n$ вершины. Напомним, что $N(v)$ множество соседей $v$ . Позволять $\sigma =(v_{1},\dots ,v_{m})$ быть списком отдельных элементов $V$ , для $v\in V\setminus \{v_{1},\dots ,v_{m}\}$ , позволять $\nu _{\sigma }(v)$ быть наименьшим $i$ такой, что $v_{i}$ является соседом $v$ , если такой $i$ существует и быть $\infty$ в противном случае.

Позволять $\sigma =(v_{1},\dots ,v_{n})$ быть перечислением вершин $V$ . Перечисление $\sigma$ называется порядком BFS (с исходным кодом $v_{1}$ ), если для всех $1<i\leq n$ , $v_{i}$ это вершина $w\in V\setminus \{v_{1},\dots ,v_{i-1}\}$ такой, что $\nu _{(v_{1},\dots ,v_{i-1})}(w)$ является минимальным. Эквивалентно, $\sigma$ является порядком BFS, если для всех $1\leq i<j<k\leq n$ с $v_{i}\in N(v_{k})\setminus N(v_{j})$ , существует сосед $v_{m}$ из $v_{j}$ такой, что $m<i$ .

Приложения

Поиск в ширину можно использовать для решения многих задач теории графов, например:

Копирование сборки мусора , алгоритм Чейни
Поиск кратчайшего пути между двумя узлами u и v , при этом длина пути измеряется количеством ребер (преимущество перед поиском в глубину ) ^[14]
(Обратный) Нумерация сетки Катхилла – Макки
Метод Форда – Фулкерсона для расчета максимального расхода в проточной сети.
Сериализация/десериализация двоичного дерева по сравнению с сериализацией в отсортированном порядке позволяет эффективно перестроить дерево.
Построение функции отказа средства сопоставления с образцом Ахо-Корасика .
Проверка двудольности графа .
Реализация параллельных алгоритмов вычисления транзитивного замыкания графа. ^[15]

См. также

Ссылки

^ то есть узел, удовлетворяющий указанному свойству
^ Кормен Томас Х.; и др. (2009). «22,3». Введение в алгоритмы . МТИ Пресс.
^ Корф, Ричард Э. (1985). «Итеративное углубление в глубину: поиск оптимального допустимого дерева» . Искусственный интеллект (27): 99–100. дои : 10.7916/D8HQ46X1 .
^ «Спецификация теста Graph500 (оценка производительности суперкомпьютера)» . Graph500.org, 2010. Архивировано из оригинала 26 марта 2015 г. Проверено 15 марта 2015 г.
^ Цузе, Конрад (1972), The Plankalkül (на немецком языке), Интернет-архив Конрада Цузе . См. стр. 96–105 связанного PDF-файла (внутренняя нумерация 2.47–2.56).
^ Мур, Эдвард Ф. (1959). «Кратчайший путь через лабиринт». Труды международного симпозиума по теории коммутации . Издательство Гарвардского университета. стр. 285–292. Цитируется Корменом, Лейзерсоном, Ривестом и Штейном.
^ Скиена, Стивен (2008). «Сортировка и поиск». Руководство по проектированию алгоритмов . Спрингер. п. 480. Бибкод : 2008адм..книга.....С . дои : 10.1007/978-1-84800-070-4_4 . ISBN 978-1-84800-069-8 .
^ Ли, Калифорния (1961). «Алгоритм соединения путей и его приложения». Транзакции IRE на электронных компьютерах (3): 346–365. дои : 10.1109/TEC.1961.5219222 . S2CID 40700386 .
^ Кормен, Томас Х. «22.2 Поиск в ширину». Введение в алгоритмы . ISBN 978-81-203-4007-7 . OCLC 1006880283 .
^ «Обход графа на основе стека ≠ поиск в глубину» . 11011110.github.io . Проверено 10 июня 2020 г.
^ Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001) [1990]. «22.2 Поиск в ширину». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр. 531–539. ISBN 0-262-03293-7 .
^ Рассел, Стюарт ; Норвиг, Питер (2003) [1995]. Искусственный интеллект: современный подход (2-е изд.). Прентис Холл. ISBN 978-0137903955 .
^ Коппин, Б. (2004). Искусственный интеллект освещен. Джонс и Бартлетт Обучение. стр. 79–80.
^ Азиз, Аднан; Пракаш, Амит (2010). «4. Алгоритмы на графах». Алгоритмы проведения собеседований . п. 144. ИСБН 978-1453792995 .
^ Дхулипала, Лаксман; Блеллок, Гай Э.; Шун, Джулиан (21 августа 2019 г.). Теоретически эффективные алгоритмы параллельных графов могут быть быстрыми и масштабируемыми . п. 17. arXiv : 1805.05208 . дои : 10.1145/3210377.3210414 . ISBN 9781450357999 . S2CID 44126609 .

Кнут, Дональд Э. (1997), Искусство компьютерного программирования, том 1. 3-е изд. , Бостон: Аддисон-Уэсли, ISBN 978-0-201-89683-1 , заархивировано из оригинала 4 сентября 2008 г. , получено 9 февраля 2008 г.

Внешние ссылки

Структуры открытых данных. Раздел 12.3.1. Поиск в ширину , Пэт Морин

[1] то есть узел, удовлетворяющий указанному свойству

[2] Кормен Томас Х.; и др. (2009). «22,3». Введение в алгоритмы . МТИ Пресс.

[3] Корф, Ричард Э. (1985). «Итеративное углубление в глубину: поиск оптимального допустимого дерева» . Искусственный интеллект (27): 99–100. дои : 10.7916/D8HQ46X1 .

[4] «Спецификация теста Graph500 (оценка производительности суперкомпьютера)» . Graph500.org, 2010. Архивировано из оригинала 26 марта 2015 г. Проверено 15 марта 2015 г.

[:0-5] Цузе, Конрад (1972), The Plankalkül (на немецком языке), Интернет-архив Конрада Цузе . См. стр. 96–105 связанного PDF-файла (внутренняя нумерация 2.47–2.56).

[6] Мур, Эдвард Ф. (1959). «Кратчайший путь через лабиринт». Труды международного симпозиума по теории коммутации . Издательство Гарвардского университета. стр. 285–292. Цитируется Корменом, Лейзерсоном, Ривестом и Штейном.

[skiena-7] Скиена, Стивен (2008). «Сортировка и поиск». Руководство по проектированию алгоритмов . Спрингер. п. 480. Бибкод : 2008адм..книга.....С . дои : 10.1007/978-1-84800-070-4_4 . ISBN 978-1-84800-069-8 .

[8] Ли, Калифорния (1961). «Алгоритм соединения путей и его приложения». Транзакции IRE на электронных компьютерах (3): 346–365. дои : 10.1109/TEC.1961.5219222 . S2CID 40700386 .

[9] Кормен, Томас Х. «22.2 Поиск в ширину». Введение в алгоритмы . ISBN 978-81-203-4007-7 . OCLC 1006880283 .

[10] «Обход графа на основе стека ≠ поиск в глубину» . 11011110.github.io . Проверено 10 июня 2020 г.

[clrs-11] Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001) [1990]. «22.2 Поиск в ширину». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр. 531–539. ISBN 0-262-03293-7 .

[12] Рассел, Стюарт ; Норвиг, Питер (2003) [1995]. Искусственный интеллект: современный подход (2-е изд.). Прентис Холл. ISBN 978-0137903955 .

[coppin-13] Коппин, Б. (2004). Искусственный интеллект освещен. Джонс и Бартлетт Обучение. стр. 79–80.

[14] Азиз, Аднан; Пракаш, Амит (2010). «4. Алгоритмы на графах». Алгоритмы проведения собеседований . п. 144. ИСБН 978-1453792995 .

[15] Дхулипала, Лаксман; Блеллок, Гай Э.; Шун, Джулиан (21 августа 2019 г.). Теоретически эффективные алгоритмы параллельных графов могут быть быстрыми и масштабируемыми . п. 17. arXiv : 1805.05208 . дои : 10.1145/3210377.3210414 . ISBN 9781450357999 . S2CID 44126609 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

v т и Структуры данных и алгоритмы
Data structures	Array Associative array Binary search tree Fenwick tree Graph Hash table Heap Linked list Queue Segment tree Stack String Tree Trie
Algorithms	Backtracking Binary search Breadth-first search Brute-force search Depth-first search Divide and conquer Dynamic programming Graph traversal Fold Greedy Hash function Minimax Online Randomized Recursion Root-finding Sorting Streaming Sweep line String-searching Topological sorting
List of data structures List of algorithms

v т и графов и деревьев Алгоритмы обхода
Search	α–β pruning A* IDA* LPA* SMA* Best-first search Beam search Bidirectional search Breadth-first search Lexicographic Parallel B* Depth-first search Iterative deepening D* Fringe search Jump point search Monte Carlo tree search SSS*
Shortest path	Bellman–Ford Dijkstra's Floyd–Warshall Johnson's Shortest path faster Yen's
Minimum spanning tree	Borůvka's Kruskal's Prim's Reverse-delete
List of graph search algorithms