Реинтерпретационная бумага
В истории физики , « О квантово-теоретическом переосмыслении кинематических и механических соотношений ».( нем .: О квантово-теоретической реинтерпретации кинематических и механических связей ), также известная как статья Uminterpretation ( переинтерпретация ) , [1] [2] была прорывной статьей в квантовой механике , написанной Вернером Гейзенбергом , которая появилась в Zeitschrift für Physik в сентябре 1925 года.
В статье Гейзенберг попытался объяснить уровни энергии одномерного ангармонического осциллятора , избегая конкретных, но ненаблюдаемых представлений об электронных орбитах, используя наблюдаемые параметры, такие как вероятности перехода для квантовых скачков , что вызвало необходимость использования двух индексов, соответствующих начальному и конечные состояния. [3]
Математически Гейзенберг показал необходимость некоммутативных операторов. Это понимание позже легло в основу принципа неопределенности Гейзенберга .
За этой статьей последовала статья Паскуаля Джордана и Макса Борна того же года: [4] и «бумага из трех человек» ( нем . Drei Herren Arbeit ) Борна, Гейзенберга и Джордана в 1926 году. [5] [1] [6] Эти статьи заложили основу матричной механики , которая пришла на смену старой квантовой теории и привела к современной квантовой механике. Гейзенберг получил Нобелевскую премию по физике в 1932 году за работу по развитию квантовой механики. [7]
Исторический контекст
[ редактировать ]Гейзенбергу было 23 года, когда он работал над статьей, выздоравливая от сенной лихорадки на острове Гельголанд с Вольфгангом Паули и переписываясь по этому поводу . Когда его спросили, что он думает о рукописи, Паули ответил положительно, но Гейзенберг сказал, что он все еще «очень не уверен в этом». В июле 1925 года он отправил рукопись Максу Борну для рассмотрения и решения, представлять ли ее для публикации. [8]
Когда Борн прочитал статью, он понял, что эту формулировку можно транскрибировать и распространить на систематический язык матриц. Борн с помощью своего помощника и бывшего ученика Паскуаля Джордана немедленно начал делать транскрипцию и расширение, и они представили свои результаты для публикации; их рукопись была получена для публикации всего через 60 дней после статьи Гейзенберга. [4] Последующая статья всех трех авторов, расширяющая теорию на множество измерений, была представлена для публикации до конца года. [5]
Гейзенберг решил основать свою квантовую механику «исключительно на отношениях между величинами, которые в принципе наблюдаемы». [9] Он заметил, что тогда нельзя было бы использовать какие-либо утверждения о таких вещах, как «положение и период обращения электрона». [10] Скорее, чтобы добиться настоящего прогресса в понимании излучения в простейшем случае, излучения возбужденных атомов водорода, нужно было работать только с измерениями частот и интенсивностей спектра ярких линий водорода.

В классической физике интенсивность каждой частоты света, производимого в излучающей системе, равна квадрату амплитуды излучения на этой частоте, поэтому внимание затем было обращено на амплитуды. Классические уравнения, которые Гейзенберг надеялся использовать для формирования квантовых теоретических уравнений, сначала давали бы амплитуды, а в классической физике интенсивности можно было вычислить, просто возведя амплитуды в квадрат. Но Гейзенберг видел, что «самым простым и естественным предположением было бы» [11] чтобы последовать примеру недавней работы Ганса Крамерса по вычислению дисперсии света . [12] Работа, которую он проделал, помогая Крамерсу в прошлом году [13] теперь дал ему важную подсказку о том, как смоделировать то, что происходит с возбужденным газообразным водородом, когда он излучает свет, и что происходит, когда падающее излучение одной частоты возбуждает атомы в дисперсионной среде, а затем энергия, переданная падающим светом, повторно излучается - иногда на исходной частоте, но часто на двух более низких частотах, сумма которых равнялась исходной частоте. Согласно их модели, электрон , который был переведен в более высокое энергетическое состояние за счет принятия энергии падающего фотона, может за один шаг вернуться в свое положение равновесия, повторно излучая фотон той же частоты, или он может вернуться через более чем один шаг, излучая один фотон на каждом этапе возвращения в состояние равновесия. Из-за того, что при выводе нового уравнения на основе этих соображений факторы сокращаются, результат оказывается относительно простым.
В рукопись также был включен коммутатор Гейзенберга , его закон умножения был необходим для описания определенных свойств атомов, в результате чего произведение двух физических величин не коммутировало . Следовательно, PQ будет отличаться от QP , где, например, P — это импульс электрона, а Q — его положение. Поль Дирак , получивший корректуру в августе 1925 года, понял, что коммутативный закон не был полностью разработан, и создал алгебраическую формулировку, чтобы выразить те же результаты в более логической форме. [14]
Правило умножения Гейзенберга
[ редактировать ]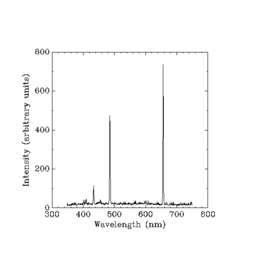
С помощью обширной серии математических аналогий, которые некоторые физики назвали «магическими», Гейзенберг выписал уравнение, которое является квантовомеханическим аналогом классического вычисления интенсивностей. Приведенное ниже уравнение встречается в статье. [15] [16] Его общий вид следующий:
что некоторый термин C должен быть вычислен путем суммирования всех произведений некоторой группы терминов A на некоторую связанную группу терминов B. Этот общий формат указывает , Потенциально будет существовать бесконечная серия терминов A и соответствующих им B. терминов Каждое из этих умножений имеет в качестве множителей два измерения, которые относятся к последовательным нисходящим переходам между энергетическими состояниями электрона. Этот тип правил отличает матричную механику от физики, знакомой в повседневной жизни, поскольку важными значениями являются то, где (в каком энергетическом состоянии или «орбитали») электрон начинается и в каком энергетическом состоянии он заканчивается, а не то, что электрон делает в то время как в том или ином состоянии.
Если, например, A и B относятся к спискам частот, расчет происходит следующим образом:
Умножьте частоту изменения энергии из состояния n в состояние n - a на частоту изменения энергии из состояния na в состояние nb. и к этому добавьте произведение, полученное путем умножения частоты изменения энергии из состояния na в состояние nb на частоту изменения энергии из состояния nb в состояние nc и так далее. Символически это:
(Согласно используемому соглашению, n - a представляет собой более высокое энергетическое состояние, чем n , поэтому переход от n к n - a будет означать, что электрон принял энергию от входящего фотона и поднялся на более высокую орбиталь, в то время как переход от n - a до n будет представлять собой электрон, падающий на более низкую орбиталь и испускающий фотон.)
Было бы легко выполнить каждый отдельный шаг этого процесса для некоторой измеряемой величины. Например, формула в рамке в начале этой статьи последовательно дает каждую необходимую длину волны. Рассчитанные значения можно легко заполнить сеткой, как описано ниже. Однако, поскольку ряд бесконечен, никто не смог выполнить всю совокупность вычислений.
Первоначально Гейзенберг разработал это уравнение, чтобы иметь возможность умножать два измерения одного и того же вида (амплитуды), поэтому не имело значения, в каком порядке они были умножены. Однако Гейзенберг заметил, что если он попытается использовать одну и ту же схему для умножения двух переменных, таких как импульс p и смещение q , то «возникает значительная трудность». [17] Оказывается, умножение матрицы p на матрицу q дает другой результат, чем умножение матрицы q на матрицу p . Разница была лишь незначительной, но эта разница никогда не могла быть уменьшена ниже определенного предела, и этот предел включал Планка постоянную h . Подробнее об этом позже. Ниже приведен очень краткий пример того, какими будут вычисления, помещенные в сетки, называемые матрицами. Учитель Гейзенберга почти сразу понял, что его работу следует выражать в матричном формате, поскольку математики уже знали, как эффективно выполнять вычисления с использованием матриц. (Поскольку Гейзенберг интересовался фотонным излучением, иллюстрации будут даны с точки зрения перехода электронов с более высокого энергетического уровня на более низкий уровень, например, n ← n -1, вместо перехода с более низкого уровня на более высокий уровень, например , п → п -1) (уравнение для сопряженных переменных: импульса и положения)
Матрица р
| Электронные состояния | нет | обратите внимание | NC | .... |
|---|---|---|---|---|
| н | п ( п︎ ← па ) | п ( п︎ ← нб ) | п ( п ︎ ← нк ) | ..... |
| нет | п ( n-a︎ ← na ) | п ( n-a︎ ← nb ) | п ( n-a︎ ← nc ) | ..... |
| обратите внимание | п ( n-b︎ ← na ) | п ( n-b︎ ← nb ) | п ( n-b︎ ← nc ) | ..... |
| переход.... | ..... | ..... | ..... | ..... |
Матрица q
| Электронные состояния | обратите внимание | NC | nd | .... |
|---|---|---|---|---|
| нет | q ( n-a︎ ← nb ) | q ( n-a︎ ← nc ) | q ( n-a︎ ← nd ) | ..... |
| обратите внимание | q ( n-b︎ ← nb ) | q ( n-b︎ ← nc ) | q ( n-b︎ ← nd ) | ..... |
| NC | q ( n-c︎ ← nb ) | q ( n-c︎ ← nc ) | q ( n-c︎ ← nd ) | ..... |
| переход.... | ..... | ..... | ..... | ..... |
Матрица произведения двух вышеупомянутых матриц, как указано соответствующим уравнением в статье Umdeutung , равна
| Электронные состояния | обратите внимание | NC | nd | ..... |
| н | А | ..... | ..... | ..... |
| нет | ..... | Б | ..... | ..... |
| обратите внимание | ..... | ..... | С | ..... |
Где
и так далее.
Если бы матрицы были перевернуты, в результате были бы получены следующие значения:
и так далее.
Развитие матричной механики
[ редактировать ]
Вернер Гейзенберг использовал идею о том, что, поскольку классическая физика права, когда она применяется к явлениям в мире вещей, больших, чем атомы и молекулы, она должна рассматриваться как частный случай более всеобъемлющей квантовой теоретической модели. Поэтому он надеялся, что сможет модифицировать квантовую физику таким образом, чтобы, когда параметры были в масштабе повседневных объектов, она выглядела точно так же, как классическая физика, но когда параметры были сведены к атомному масштабу, разрывы наблюдались в таких вещах, как широко разнесенные частоты видимого спектра ярких линий водорода снова вернутся в поле зрения.
Единственное, что люди в то время больше всего хотели понять в отношении излучения водорода, — это как предсказать или объяснить интенсивность линий в его спектре. Хотя Гейзенберг в то время этого не знал, общий формат, который он разработал для выражения своего нового способа работы с квантово-теоретическими вычислениями, может служить рецептом для двух матриц и способов их умножения. [18]
В статье Umdeutung матрицы не упоминаются. Большим достижением Гейзенберга стала «схема, которая была способна в принципе однозначно определять соответствующие физические свойства (частоты и амплитуды переходов)». [19] водородного излучения.
После того как Гейзенберг написал статью «Umdeutung» , он передал ее одному из своих старших коллег для внесения необходимых исправлений и ушел в отпуск. Макс Борн ломал голову над уравнениями и некоммутирующими уравнениями, которые Гейзенберг находил хлопотными и тревожащими. Через несколько дней он понял, что эти уравнения представляют собой инструкции по выписыванию матриц. [20]
Рассмотрев... примеры... [Гейзенберг] нашел это правило... Это было летом 1925 года. Гейзенберг... взял отпуск... и передал мне свою статью для публикации... ..Правило умножения Гейзенберга не давало мне покоя, и после недели интенсивных размышлений и проб я внезапно вспомнил об алгебраической теории....Такие квадратичные массивы хорошо знакомы математикам и называются матрицами в связи с определенным правилом. умножения. Я применил это правило к квантовому условию Гейзенберга и обнаружил, что оно справедливо для диагональных элементов. Несложно было догадаться, какими должны быть остальные элементы, а именно нулевые; и тотчас передо мной предстала странная формула
Символ Q — это матрица смещения, P — матрица импульса, i — квадратный корень из отрицательного , а h — постоянная Планка. [21] Борн и несколько его коллег взяли на себя задачу разработать все в матричной форме до того, как Гейзенберг вернулся из отпуска, и через несколько месяцев новая квантовая механика в матричной форме легла в основу другой статьи. Гейзенберга Это соотношение теперь известно как принцип неопределенности .
Когда такие величины, как положение и импульс, упоминаются в контексте матричной механики Гейзенберга, такое утверждение, как pq ≠ qp, относится не к одному значению p и одному значению q, а к матрице (сетке значений, расположенных в определенном порядке). способ) значений положения и матрицу значений импульса. Таким образом, умножение p на q или q на p на самом деле означает матричное умножение двух матриц. Если перемножить две матрицы, ответом будет третья матрица.
Поль Дирак решил, что суть работы Гейзенберга заключается в той самой особенности, которую Гейзенберг первоначально считал проблематичной, - в факте некоммутативности, например, между умножением матрицы импульса на матрицу смещения и умножением матрицы смещения на матрицу импульса. . Это понимание привело Дирака в новых и продуктивных направлениях. [22]
См. также
[ редактировать ]Ссылки
[ редактировать ]- Эйчисон, Ян-младший; Макманус, Дэвид А.; Снайдер, Томас М. (2004). «Понимание «волшебной» статьи Гейзенберга от июля 1925 года: новый взгляд на детали вычислений». Американский журнал физики . 72 (11): 1370–1379. arXiv : Quant-ph/0404009 . Бибкод : 2004AmJPh..72.1370A . дои : 10.1119/1.1775243 . S2CID 53118117 . Прямая загрузка Aitchison et al. по этому поводу.
- Дирак, ПАМ (1925). «Основные уравнения квантовой механики» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 109 (752): 642–653. Бибкод : 1925RSPSA.109..642D . дои : 10.1098/rspa.1925.0150 . ISSN 0950-1207 . JSTOR 94441 . Решающий синтез реинтерпретации статьи Гейзенберга, который вводит современный язык, используемый сейчас.
- БЛВан дер Варден (2007). Источники квантовой механики . Дуврские публикации. ISBN 978-0486458922 .
- ^ Jump up to: а б Дункан, Энтони; Янссен, Мишель (2023). «Записка Гейзенберга Umdeutung». Построение квантовой механики . Том. 2. Оксфорд: Оксфорд Академик. стр. 209–254. дои : 10.1093/oso/9780198883906.003.0004 . ISBN 978-0-19-888390-6 .
- ^ Краг, Хельге (3 мая 2012 г.). Нильс Бор и квантовый атом: модель атомной структуры Бора 1913-1925 гг . ОУП Оксфорд. ISBN 978-0-19-163046-0 .
- ^ Эмилио Сегре, От рентгеновских лучей до кварков: современные физики и их открытия . WH Freeman and Company, 1980. ISBN 0-7167-1147-8 , стр. 153–157.
- ^ Jump up to: а б М. Борн и П. Джордан, О квантовой механике , Journal of Physics , 34 , 858–888, 1925 (получено 27 сентября 1925 г.). [Английский перевод: Б.Л. ван дер Варден, редактор, «Источники квантовой механики» . Дуврские публикации, 1968. ISBN 0-486-61881-1 ].
- ^ Jump up to: а б М. Борн, В. Гейзенберг и П. Джордан, О квантовой механике II , Journal of Physics , 35 , 557–615, 1925 (получено 16 ноября 1925 г.). [Английский перевод: Б.Л. ван дер Варден, редактор журнала «Источники квантовой механики». Дуврские публикации, 1968. ISBN 0-486-61881-1 ].
- ^ Физика, Американский институт. «Гейзенберг/Неопределенность» . History.aip.org . Проверено 5 марта 2024 г.
- ^ «Нобелевская премия по физике 1932 года» . NobelPrize.org . Проверено 5 марта 2024 г.
- ^ Мехра, Джагдиш ; Рехенберг, Гельмут (1982). Формулировка матричной механики и ее модификаций 1925–1926 гг . Историческое развитие квантовой теории. Спрингер. ISBN 0-387-90675-4 .
- ^ BLVan der Waerden 2007 , с. 261
- ^ BLVan der Waerden 2007 , с. 261
- ^ BLVan der Waerden 2007 , с. 275 ф
- ^ Крамерс, Х.А. (1924). «Закон дисперсии и теория спектров Бора» . Природа . 113 (2845): 673–674. Бибкод : 1924Natur.113..673K . дои : 10.1038/113673a0 . ISSN 0028-0836 . S2CID 4138614 .
- ^ BLVan der Waerden 2007 , статья 3
- ^ Краг, Х. (2004). «Дирак, Поль Адриен Морис (1902–1984)». Оксфордский национальный биографический словарь . Издательство Оксфордского университета.
- ^ BLVan der Waerden 2007 , с. 266
- ^ В статье Эйчисона и др. это уравнение (10) на странице 5.
- ^ BLVan der Waerden 2007 , с. 266 и др.
- ↑ Статья Гейзенберга 1925 года переведена в BLVan der Waerden (2007) , где она представлена в главе 12.
- ^ Эйтчисон и др., «Понимание« волшебной » статьи Гейзенберга от июля 1925 года: новый взгляд на детали вычислений», стр. 2
- ^ Нобелевская лекция Борна, цитируемая в книге Томаса Ф. Джордана «Квантовая механика в простой матричной форме», стр. 6
- ^ См . Введение в квантовую механику . Хенрик Смит, с. 58 за читабельное введение. Математический вывод этого соотношения см. Яна Дж. Р. Эйтчисона и др., «Понимание «магической» статьи Гейзенберга от июля 1925 года», Приложение А.
- ^ Томас Ф. Джордан, Квантовая механика в простой матричной форме , с. 149
Дальнейшее чтение
[ редактировать ]- Вернер Гейзенберг (1925). «О квантово-теоретической интерпретации кинематических и механических связей» (PDF) . Журнал физики (на немецком языке). 33 (1): 879–893. Бибкод : 1925ZPhy...33..879H . дои : 10.1007/BF01328377 . S2CID 186238950 .
- Английский перевод «Квантово-теоретическая реинтерпретация кинематических и механических отношений» Б.Л. ван дер Вардена можно найти в Б.Л. ван дер Варден, изд. (1968). Источники квантовой механики . Нью-Йорк: Дувр. стр. 261–276. ISBN 0-486-61881-1 .



