Теория импульса элемента лопасти

Теория импульса элемента лопасти — это теория, которая сочетает в себе теорию элемента лопасти и теорию импульса . Он используется для расчета местных сил на лопасти винта или ветряной турбины. Теория элемента лопасти объединена с теорией импульса, чтобы облегчить некоторые трудности при расчете индуцированных скоростей ротора.

В этой статье особое внимание уделяется применению теории элементов лопастей к наземным ветряным турбинам, но эти принципы применимы и к гребным винтам. В то время как площадь обтекаемой трубы уменьшается за счет пропеллера, она увеличивается за счет ветряной турбины. Для любого применения весьма упрощенным, но полезным приближением является модель Ренкина - Фруда «импульс» или «приводной диск» (1865, 1889 ). В этой статье объясняется применение «предела Бетца» к эффективности наземной ветряной турбины.

Теория элемента лезвия Фруда (1878 г.) — это математический процесс определения поведения винтов , позже уточненный Глауэртом (1926). Бетц (1921) внес приблизительную поправку к теории импульса «приводного диска Рэнкина – Фруда». для учета внезапного вращения, сообщаемого потоку приводным диском (NACA TN 83, «Теория винтового гребного винта» и NACA TM 491, «Проблемы гребного винта»). В теории импульса элемента лопасти в модель включен угловой момент, а это означает, что след (воздух после взаимодействия с ротором) имеет угловой момент. То есть воздух начинает вращаться вокруг оси Z сразу при взаимодействии с ротором (см. схему ниже). Необходимо учитывать угловой момент, поскольку ротор, который представляет собой устройство, извлекающее энергию из ветра, вращается в результате взаимодействия с ветром.

Модель Рэнкина – Фруда

«Предел Бетца», еще не использующий вклад Бетца для учета вращательного потока с упором на пропеллеры, применяет теорию « приводного диска » Ренкина-Фруда для получения максимальной эффективности стационарной ветряной турбины. Следующий анализ ограничивается осевым движением воздуха:

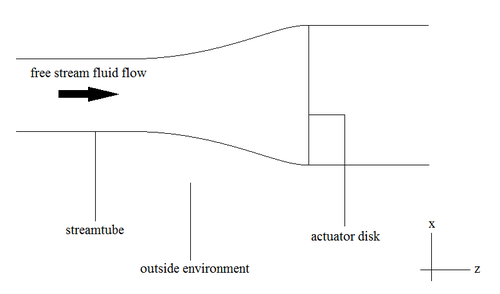
В нашей трубе потока жидкость течет слева направо, а приводной диск представляет собой ротор. Будем считать, что ротор бесконечно тонкий. Сверху мы видим, что в начале трубы поток жидкости перпендикулярен диску привода. Жидкость взаимодействует с ротором, передавая таким образом энергию от жидкости ротору. Затем жидкость продолжает течь вниз по течению. Таким образом, мы можем разбить нашу систему/трубу потока на две части: диск до актуатора и диск после актуатора. До взаимодействия с ротором полная энергия в жидкости постоянна. Более того, после взаимодействия с ротором полная энергия жидкости остается постоянной.

Уравнение Бернулли описывает различные формы энергии, присутствующие в потоке жидкости, где чистая энергия постоянна, т.е. когда жидкость не передает никакой энергии какому-либо другому объекту, например ротору. Энергия состоит из статического давления , гравитационной потенциальной энергии и кинетической энергии . Математически мы имеем следующее выражение:

${\frac {1}{2}}\rho v^{2}+P+\rho gh={\text{const.}}$

где $\rho$ - плотность жидкости, $v$ - скорость жидкости вдоль линии тока, $P$ – энергия статического давления, $g$ - ускорение свободного падения, а $h$ это высота над землей. Для целей этого анализа мы предположим, что гравитационная потенциальная энергия неизменна во время течения жидкости слева направо, поэтому мы имеем следующее:

${\frac {1}{2}}\rho v^{2}+P=\mathrm {const.}$

Таким образом, если у нас есть две точки на линии тока, точка 1 и точка 2, и в точке 1 скорость жидкости вдоль линии тока равна $v_{1}$ и давление в точке 1 равно $P_{1}$, а в точке 2 скорость жидкости вдоль линии тока равна $v_{2}$ и давление в точке 2 равно $P_{2}$, и никакая энергия не была извлечена из жидкости между точками 1 и 2, то мы имеем следующее выражение:

${\frac {1}{2}}\rho v_{1}^{2}+P_{1}={\frac {1}{2}}\rho v_{2}^{2}+P_{2}$

Теперь вернемся к нашей исходной схеме. Учитывайте поток перед приводом. Далеко вверх по течению скорость жидкости равна $v_{\infty }$; затем скорость жидкости уменьшается, а давление увеличивается по мере приближения к ротору. В соответствии с законом сохранения массы массовый расход через ротор должен быть постоянным. Массовый расход, ${\dot {m}}$, через поверхность площади $A$ задается следующим выражением:

${\dot {m}}=\rho Av$

где $\rho$ плотность и $v$ – скорость жидкости вдоль линии тока. Таким образом, если массовый расход постоянен, увеличение площади должно приводить к уменьшению скорости жидкости вдоль линии тока. Это означает, что кинетическая энергия жидкости уменьшается. Если поток расширяется, но не передает энергию, то применяется Бернулли. Таким образом, уменьшению кинетической энергии противодействует увеличение энергии статического давления.

Итак, перед ротором мы имеем следующую ситуацию: далеко вверх по потоку давление жидкости такое же, как атмосферное, $P_{\infty }$; непосредственно перед взаимодействием с ротором давление жидкости увеличилось, и поэтому кинетическая энергия уменьшилась. Математически это можно описать с помощью уравнения Бернулли:

${\frac {1}{2}}\rho v_{\infty }^{2}+P_{\infty }={\frac {1}{2}}\rho \left(v_{\infty }(1-a)\right)^{2}+P_{D+}$

где мы записали скорость жидкости на роторе как $v_{\infty }(1-a)$, где $a$ – коэффициент осевой индукции. Давление жидкости на входной стороне приводного диска равно $P_{D+}$. Мы рассматриваем ротор как бесконечно тонкий исполнительный диск. Таким образом, мы предполагаем, что скорость жидкости на диске привода не изменяется. Поскольку энергия была извлечена из жидкости, давление должно было уменьшиться.

Теперь рассмотрим постротор: сразу после взаимодействия с ротором скорость жидкости по-прежнему равна $v_{\infty }(1-a)$, но давление упало до значения $P_{D-}$; далеко ниже по течению давление жидкости достигло равновесия с атмосферой; это было достигнуто в естественном и динамически медленном процессе уменьшения скорости потока в струйной трубке для поддержания динамического равновесия (т.е. $P\rightarrow P_{\infty }$ далеко вниз по течению. Предполагая отсутствие дальнейшей передачи энергии, мы можем применить Бернулли для нисходящего потока:

${\frac {1}{2}}\rho \left(v_{\infty }(1-a)\right)^{2}+P_{D-}={\frac {1}{2}}\rho v_{w}^{2}+P_{\infty }$

где

$v_{w}=$ Скорость далеко вниз по течению в следе

Таким образом, мы можем получить выражение для разницы давлений между передней и задней частью ротора:

$P_{D+}-P_{D-}={\frac {1}{2}}\rho (v_{\infty }^{2}-v_{w}^{2})$

Если у нас есть разница давлений по площади приводного диска, то на приводной диск действует сила, которую можно определить по формуле $F=\Delta PA$:

${\frac {1}{2}}\rho (v_{\infty }^{2}-v_{w}^{2})A_{D}$

где $A_{D}$ – площадь приводного диска. Если ротор — единственное, что поглощает энергию из жидкости, скорость изменения осевого момента жидкости — это сила, действующая на ротор. Скорость изменения осевого момента можно выразить как разность начальной и конечной осевых скоростей жидкости, умноженную на массовый расход:

$F={\frac {\mathrm {d} p}{\mathrm {d} t}}={\dot {m}}(v_{\infty }-v_{w})=\rho A_{D}v_{D}(v_{\infty }-v_{w})=\rho A_{D}(1-a)v_{\infty }(v_{\infty }-v_{w})$

Таким образом, мы можем прийти к выражению для скорости жидкости далеко вниз по течению:

$v_{w}=(1-2a)v_{\infty }$

Эта сила действует на ротор. Мощность, отбираемая у жидкости, равна силе, действующей на жидкость, умноженной на скорость жидкости в точке отбора мощности:

$\mathrm {Power} _{ext}=Fv_{D}=2a(1-a)^{2}v_{\infty }^{3}\rho A_{D}$

Максимальная мощность

Предположим, мы заинтересованы в поиске максимальной мощности, которую можно извлечь из жидкости. Мощность в жидкости определяется следующим выражением:

$\mathrm {Power} ={\frac {1}{2}}\rho Av^{3}$

где $\rho$ - плотность жидкости, как и раньше, $v$ - скорость жидкости, а $A$ — площадь воображаемой поверхности, по которой течет жидкость. Мощность, извлекаемая из жидкости ротором в описанном выше сценарии, составляет некоторую часть этого выражения мощности. Назовем дробь коэффициентом мощности, $C_{p}$. Таким образом, извлекаемая сила, $\mathrm {Power} _{ext}$ задается следующим выражением:

$\mathrm {Power} _{ext}=\mathrm {Power} \times C_{p}$

Наш вопрос заключается в следующем: каково максимальное значение $C_{p}$ используя модель Бетца?

Вернемся к полученному нами выражению для мощности, передаваемой от жидкости к ротору ( $\mathrm {Power} _{ext}$). Мы видим, что извлекаемая мощность зависит от коэффициента осевой индукции. Если мы дифференцируем $\mathrm {Power} _{ext}$ относительно $a$, мы получим следующий результат:

${\frac {\mathrm {d} \mathrm {Power} _{ext}}{\mathrm {d} a}}=2v_{\infty }^{3}\rho A_{D}\times \left((1-a)^{2}-2a(1-a)\right)$

Если мы максимизировали отбор энергии, мы можем установить вышеприведенное значение равным нулю. Это позволяет нам определить стоимость $a$ что обеспечивает максимальную отдачу мощности. Это значение является $1/3$. Таким образом, мы можем найти это $C_{P~max}=16/27$. Другими словами, ротор не может извлечь более 59 процентов мощности жидкости.

Теория импульса элемента лопасти

По сравнению с моделью Рэнкина-Фруда, теория импульса элемента Blade учитывает угловой момент ротора. Рассмотрим левую часть рисунка ниже. У нас есть труба потока, в которой находится жидкость и ротор. Будем считать, что между содержимым струйной трубки и всем, что находится за ее пределами, взаимодействия нет. То есть мы имеем дело с изолированной системой. В физике изолированные системы должны подчиняться законам сохранения. Примером такого явления является сохранение углового момента. Таким образом, угловой момент внутри трубы потока должен сохраняться. Следовательно, если ротор приобретает угловой момент в результате взаимодействия с жидкостью, что-то еще должно приобрести равный и противоположный угловой момент. Как уже говорилось, система состоит только из жидкости и ротора, жидкость должна приобретать угловой момент в следе. Поскольку мы связали изменение осевого момента с некоторым коэффициентом индукции $a$, будем связывать изменение углового момента жидкости с коэффициентом тангенциальной индукции, $a'$.

Рассмотрим следующую настройку.

Разобьем область ротора на кольцевые кольца бесконечно малой толщины. Мы делаем это для того, чтобы можно было предположить, что коэффициенты осевой индукции и коэффициенты тангенциальной индукции постоянны по всему кольцевому кольцу. Предположением этого подхода является то, что кольцевые кольца независимы друг от друга, т.е. нет взаимодействия между жидкостями соседних кольцевых колец.

Бернулли для вращающегося следа

Вернемся теперь к Бернулли:

${\frac {1}{2}}\rho v_{1}^{2}+P_{1}={\frac {1}{2}}\rho v_{2}^{2}+P_{2}$

Скорость – это скорость жидкости вдоль линии тока. Линия тока не обязательно может проходить параллельно определенной оси координат, например оси Z. Таким образом, скорость может состоять из компонент в осях, составляющих систему координат. Для этого анализа мы будем использовать цилиндрические полярные координаты. $(r,~\theta ,~z)$. Таким образом $v^{2}=v_{r}^{2}+v_{\theta }^{2}+v_{z}^{2}$.

ПРИМЕЧАНИЕ. Фактически мы будем работать в цилиндрических координатах для всех аспектов, например $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\theta }}+F_{z}{\hat {\mathbf {z} }}$

Теперь рассмотрим установку, показанную выше. Как и раньше, мы можем разбить установку на два компонента: восходящий и нисходящий.

Преротор

$P_{\infty }+{\frac {1}{2}}\rho v_{u}^{2}=P_{D+}+{\frac {1}{2}}\rho v_{D}^{2}$

где $v_{u}$ - скорость жидкости вдоль линии тока далеко вверх по течению, а $v_{D}$ - скорость жидкости непосредственно перед ротором. Записанное в цилиндрических полярных координатах, мы имеем следующее выражение:

$P_{\infty }+{\frac {1}{2}}\rho v_{\infty }^{2}=P_{D+}+{\frac {1}{2}}\rho (v_{\infty }(1-a))^{2}$

где $v_{\infty }$ и $v_{\infty }(1-a)$ — z-компоненты скорости далеко вверх по потоку и непосредственно перед ротором соответственно. Это точно то же самое, что и уравнение восходящего потока модели Бетца.

Как видно из рисунка выше, поток расширяется по мере приближения к ротору, что является следствием увеличения статического давления и сохранения массы. Это означало бы, что $v_{r}\neq 0$ вверх по течению. Однако для целей настоящего анализа этим эффектом можно пренебречь.

Пост-ротор

$P_{D-}+{\frac {1}{2}}\rho v_{D}^{2}=P_{\infty }+{\frac {1}{2}}\rho v_{w}^{2}$

где $v_{D}$ — скорость жидкости сразу после взаимодействия с ротором. Это можно записать как $v_{D}^{2}=v_{D,~r}^{2}+v_{D,~\theta }^{2}+v_{D,~z}^{2}$. Радиальная составляющая скорости будет равна нулю; это должно быть правдой, если мы хотим использовать кольцевой подход; предположение об обратном означало бы столкновение между кольцевыми кольцами в какой-то точке ниже по потоку. Поскольку мы предполагаем, что осевая скорость диска не меняется, $v_{D,~z}=(1-a)v_{\infty }$. Угловой момент должен сохраняться в изолированной системе. При этом вращение следа не должно затухать. Таким образом $v_{\theta }$ в нижнем участке постоянно. Таким образом, Бернулли упрощает следующую часть:

$P_{D-}+{\frac {1}{2}}\rho v_{D,~z}^{2}=P_{\infty }+{\frac {1}{2}}\rho v_{w,~z}^{2}=P_{D-}+{\frac {1}{2}}\rho (v_{\infty }(1-a))^{2}$

Другими словами, уравнения Бернулли до и после ротора такие же, как выражения Бернулли в модели Бетца. Следовательно, мы можем использовать такие результаты, как отбор мощности и скорость следа, полученные в модели Бетца, т.е.

$v_{w,z}=(1-2a)v_{\infty }$

$\mathrm {Power} =2a(1-a)^{2}v_{\infty }^{3}\rho A_{D}$

Это позволяет нам рассчитать максимальную отбираемую мощность для системы, включающей вращающийся след. Можно показать, что это дает то же значение, что и модель Бетца, т.е. 0,59. Этот метод предполагает признание того, что крутящий момент, создаваемый ротором, определяется следующим выражением:

$\delta \mathbf {Q} =2\pi r\delta r\times \rho U_{\infty }(1-a)\times 2a'r\omega$

с необходимыми терминами, определенными непосредственно ниже.

Силы лезвия

Рассмотрим течение жидкости вокруг профиля. Поток жидкости вокруг профиля создает подъемную силу и силы сопротивления. По определению, подъемная сила — это сила, действующая на аэродинамический профиль перпендикулярно кажущейся скорости потока жидкости, наблюдаемой аэродинамическим профилем. Сопротивление — это силы, действующие по касательной к кажущейся скорости потока жидкости, наблюдаемой аэродинамическим профилем. Что мы подразумеваем под кажущейся скоростью? Рассмотрим диаграмму ниже:

Скорость, воспринимаемая лопастью ротора, зависит от трех факторов: осевой скорости жидкости, $v_{\infty }(1-a)$; тангенциальная скорость жидкости из-за ускорения вокруг аэродинамического профиля, $a'\omega r$; и само движение ротора, $\omega r$. То есть кажущаяся скорость жидкости определяется следующим образом:

$\mathbf {v} =\omega r(1+a'){\hat {\mathbf {\theta } }}+v_{\infty }(1-a){\hat {\mathbf {z} }}$

Таким образом, скорость вымпельного ветра равна величине этого вектора, т.е.:

$|\mathbf {v} |^{2}=(\omega r(1+a'))^{2}+(v_{\infty }(1-a))^{2}=W^{2}$

Мы также можем определить угол $\phi$ из рисунка выше:

$\sin \phi ={\frac {v_{\infty }(1-a)}{W}}$

Предположим, мы знаем угол $\beta$, тогда мы сможем поработать $\alpha$ просто используя соотношение $\alpha =\phi -\beta$; затем мы можем вычислить коэффициент подъемной силы, $c_{L}$и коэффициент сопротивления $c_{D}$, из которого мы можем определить подъемную силу и силы сопротивления, действующие на лопасть.

Рассмотрим кольцевое кольцо, частично занятое лопаточными элементами. Длина каждой секции лопатки, занимающей кольцевое кольцо, равна $\delta r$ (см. рисунок ниже).

Подъемная сила, действующая на те части лопастей/профилей, каждая из которых имеет хорду. $c$ задается следующим выражением:

$\delta L={\frac {1}{2}}\rho NW^{2}c\times c_{L}(\alpha )\delta r$

где $c_{L}$ - коэффициент подъемной силы, который является функцией угла атаки, и $N$ это количество лопастей. Кроме того, сопротивление, действующее на часть лопастей/профилей с хордой $c$ задается следующим выражением:

$\delta D={\frac {1}{2}}\rho NW^{2}c\times c_{D}(\alpha )\delta r$

Помните, что эти рассчитанные силы являются нормальными и касательными к кажущейся скорости. Нас интересуют силы ${\hat {\mathbf {z} }}$ и ${\hat {\theta }}$ оси. Таким образом, нам нужно рассмотреть диаграмму ниже:

Таким образом мы можем увидеть следующее:

$\delta F_{\theta }=\delta L\sin \phi -\delta D\cos \phi$

$\delta F_{z}=\delta L\cos \phi +\delta D\sin \phi$

$F_{\theta }$ – сила, отвечающая за вращение лопастей несущего винта; $F_{z}$ - сила, которая отвечает за изгиб лопастей.

Напомним, что для изолированной системы суммарный момент импульса системы сохраняется. Если ротор приобрел угловой момент, то же самое должна сделать и жидкость в следе. Предположим, что жидкость в следе приобретает тангенциальную скорость $v_{\theta }=2a'\omega r$. Таким образом, крутящий момент в воздухе определяется выражением

$|\mathbf {\delta {Q}} |=\rho (2\pi r\delta r)U_{\infty }(1-a)\times (2\Omega a'r^{2})$

Благодаря сохранению углового момента это уравновешивает крутящий момент лопастей ротора; таким образом,

${\frac {1}{2}}\rho W^{2}Nc(c_{l}\sin \phi -c_{d}\cos \phi )r\delta r=\rho (2\pi r\delta r)U_{\infty }(1-a)\times (2\Omega a'r^{2})$

${\frac {1}{2}}W^{2}Nc(c_{l}\sin \phi -c_{d}\cos \phi )=4\pi U_{\infty }(1-a)\times \Omega a'r^{2}$

Кроме того, скорость изменения линейного момента в воздухе уравновешивается изгибающей силой вне плоскости, действующей на лопасти: $\delta F_{z}$. Согласно теории импульса, скорость изменения импульса в воздухе следующая:

$\delta F_{z}=\rho (2\pi r\delta r)U_{\infty }(1-a)\times (v_{\infty }-v_{w})$

что может быть выражено как

$\delta F_{z}=\rho (4\pi r\delta r)U_{\infty }^{2}a(1-a)$

Уравновешивание этого с силой изгиба вне плоскости дает

${\frac {1}{2}}W^{2}Nc(c_{l}\cos \phi +c_{d}\sin \phi )=\rho (4\pi r\delta r)U_{\infty }^{2}a(1-a)$

Теперь дадим следующие определения:

$C_{y}=c_{l}\sin \phi -c_{d}\cos \phi$

$C_{x}=c_{l}\cos \phi +c_{d}\sin \phi$

Итак, мы имеем следующие уравнения:

${\frac {1}{2}}W^{2}NcC_{y}=4\pi U_{\infty }(1-a)\times \Omega a'r^{2}$ ( 1 )

${\frac {1}{2}}\rho W^{2}NcC_{x}=4\pi \rho \left[(a'\Omega r)^{2}+U_{\infty }^{2}a(1-a)\right]r$ ( 2 )

Давайте обратимся к следующему уравнению, которое можно увидеть из анализа приведенного выше рисунка:

$\sin \phi ={\frac {U_{\infty }}{W}}(1-a)\rightarrow \sin ^{2}\phi =\left({\frac {U_{\infty }}{W}}(1-a)\right)^{2}$ ( 3 )

Таким образом, с помощью этих трех уравнений путем некоторых алгебраических манипуляций можно получить следующий результат:

${\frac {a}{1-a}}={\frac {C_{x}\sigma _{r}}{4\sin ^{2}\phi }}$

Мы можем вывести выражение для $a'$ аналогичным образом. Это позволяет нам понять, что происходит с ротором и жидкостью. Уравнения такого типа затем решаются итерационными методами.

Допущения и возможные недостатки БЭМ-моделей

• Предполагается, что каждое кольцевое кольцо независимо от любого другого кольцевого кольца.
• Не учитывает расширение следа.
• Не учитывает потери на кончиках , хотя могут быть включены поправочные коэффициенты.
• Не учитывает yaw , хотя это можно сделать.
• На основе устойчивого потока (нетурбулентного).