Теорема Кенига (теория графов)

Теорему о бесконечных графах см. в лемме Кенига . Чтобы узнать о других значениях, см. теорему Кенига (значения) .

Пример двудольного графа с максимальным совпадением (синий) и минимальным покрытием вершин (красный) размера шесть.

В математической области графов теории теорема Кенига , доказанная Денесом Кенигом ( 1931 ), описывает эквивалентность между проблемой максимального соответствия и проблемой минимального вершинного покрытия в двудольных графах . Он был открыт независимо, также в 1931 году, Йене Эгервари в более общем случае взвешенных графов .

Параметр

Вершинное покрытие в графе — это набор вершин, который включает хотя бы одну конечную точку каждого ребра, и вершинное покрытие является минимальным, если ни одно другое вершинное покрытие не имеет меньшего количества вершин. Паросочетание в графе — это набор ребер, ни одно из которых не имеет общей конечной точки, и паросочетание является максимальным , если ни одно другое паросочетание не имеет больше ребер.

Из определения очевидно, что любое множество вершин-покрытий должно быть не меньше любого совпадающего множества (поскольку для каждого ребра в сопоставлении необходима хотя бы одна вершина в покрытии). В частности, минимальный набор покрытий вершин по крайней мере такой же большой, как и максимальный набор совпадающих . Теорема Кенига утверждает, что в любом двудольном графе минимальное множество покрытий вершин и максимальное множество совпадающих фактически имеют одинаковый размер.

Формулировка теоремы

В любом двудольном графе количество ребер в максимальном паросочетании равно числу вершин в минимальном вершинном покрытии .

Пример

Двудольный граф, показанный на рисунке выше, имеет 14 вершин; паросочетание с шестью ребрами показано синим цветом, а вершинное покрытие с шестью вершинами показано красным. Не может быть меньшего вершинного покрытия, потому что любое вершинное покрытие должно включать хотя бы одну конечную точку каждого совпадающего ребра (а также любого другого ребра), так что это минимальное вершинное покрытие. Точно так же не может быть большего сопоставления, поскольку любое совпадающее ребро должно включать хотя бы одну конечную точку в вершинном покрытии, поэтому это максимальное сопоставление. Теорема Кенига утверждает, что равенство между размерами паросочетания и покрытия (в этом примере оба числа равны шести) применимо в более общем смысле к любому двудольному графу.

Доказательства

Конструктивное доказательство

Минимальный разрез $(S,T)$ в проточной сети $G'_{\infty }$

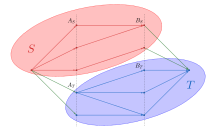
Следующее доказательство предлагает способ построения минимального вершинного покрытия из максимального паросочетания. Позволять $G=(V,E)$ — двудольный граф и пусть $A,B$ быть двумя частями множества вершин $V$. Предположим, что $M$ является максимальным соответствием для $G$.

Постройте сеть потока $G'_{\infty }$ получено из $G$ таким образом, чтобы были края емкости $1$ из источника $s$ к каждой вершине $a\in A$ и из каждой вершины $b\in B$ в раковину $t$, и мощности $+\infty$ от $a$ к $b$ для любого $(a,b)\in E$.

Размер $|M|$ максимального соответствия в $G$ это размер максимального потока в $G'_{\infty }$, что, в свою очередь, представляет собой размер минимального разреза в сети $G'_{\infty }$, как следует из теоремы о максимальном потоке и минимальном разрезе .

Позволять $(S,T)$ быть минимальный разрез. Позволять $A=A_{S}\cup A_{T}$ и $B=B_{S}\cup B_{T}$, такой, что $A_{S},B_{S}\subset S$ и $A_{T},B_{T}\subset T$. Тогда минимальный разрез состоит только из ребер, идущих от $s$ к $A_{T}$ или из $B_{S}$ к $t$, как любое ребро из $A_{S}$ к $B_{T}$ сделало бы размер разреза бесконечным.

Следовательно, размер минимального разреза равен $|A_{T}|+|B_{S}|$. С другой стороны, $A_{T}\cup B_{S}$ является вершинным покрытием, так как любое ребро, не инцидентное вершинам из $A_{T}$ и $B_{S}$ должно быть инцидентно паре вершин из $A_{S}$ и $B_{T}$, что противоречило бы факту отсутствия ребер между $A_{S}$ и $B_{T}$.

Таким образом, $A_{T}\cup B_{S}$ является минимальным вершинным покрытием $G$.

Конструктивное доказательство без концепций потока

Ни одна вершина в вершинном покрытии не может покрывать более одного ребра. $M$ (поскольку полуперекрытие края помешало бы $M$ изначально не является паросочетанием), поэтому, если вершина, покрывающая $|M|$ вершины могут быть построены, это должно быть минимальное покрытие.

Для построения такого покрытия пусть $U$ быть набором несовпадающих вершин в $A$ (возможно, пустое), и пусть $Z$ — множество вершин, которые либо находятся в $U$ или связаны с $U$ путем чередования путей (пути, которые чередуются между ребрами, входящими в сопоставление, и ребрами, которые не входят в сопоставление). Позволять

$K=(A\setminus Z)\cup (B\cap Z).$

Каждый край $e$ в $E$ либо принадлежит альтернативному пути (и имеет правую конечную точку в $K$), или он имеет левую конечную точку в $K$. Ибо, если $e$ совпадает, но не находится в альтернативном пути, то его левая конечная точка не может находиться в альтернативном пути (поскольку два совпадающих ребра не могут иметь общую вершину) и, таким образом, принадлежит $A\setminus Z$. Альтернативно, если $e$ не имеет совпадения, но не находится в альтернативном пути, то его левая конечная точка не может находиться в альтернативном пути, поскольку такой путь можно расширить, добавив $e$ к этому. Таким образом, $K$ образует вершинное покрытие.

Кроме того, каждая вершина в $K$ является конечной точкой совпадающего ребра. Ибо каждая вершина в $A\setminus Z$ совпадает, потому что $Z$ представляет собой надмножество $U$, набор несовпадающих левых вершин. И каждая вершина в $B\cap Z$ также должны быть сопоставлены, поскольку если бы существовал альтернативный путь к несовпадающей вершине, то изменение сопоставления путем удаления совпадающих ребер из этого пути и добавления несовпадающих ребер на их место увеличило бы размер сопоставления. Однако ни одно совпадающее ребро не может иметь обе конечные точки в $K$. Таким образом, $K$ является вершинным покрытием мощности, равной $M$, и должно быть минимальным вершинным покрытием.

Доказательство с использованием двойственности линейного программирования.

Чтобы объяснить это доказательство, нам сначала нужно расширить понятие паросочетания до понятия дробного паросочетания — присвоения веса в [0,1] каждому ребру так, чтобы сумма весов вблизи каждой вершины была не более 1. (целочисленное паросочетание — это частный случай дробного паросочетания, в котором веса находятся в {0,1}). Аналогичным образом мы определяем дробное вершинное-покрытие - присвоение неотрицательного веса каждой вершине такое, что сумма весов в каждом ребре равна не менее 1 (целое вершинное-покрытие - это частный случай дробного вершинного-покрытия в котором веса находятся в {0,1}).

Максимальный размер дробного соответствия на графике $G=(V,E)$ является решением следующей линейной программы :

Максимизировать 1 _E · x

При условии: x ≥ 0 _E

__________ А _Г · x ≤ 1 _В .

где x — вектор размера | Е | в котором каждый элемент представляет вес ребра в дробном сопоставлении. 1 _E — вектор | Е | единицы, поэтому первая строка указывает размер соответствия. 0 _E — вектор | Е | нули, поэтому вторая строка указывает на ограничение, согласно которому веса неотрицательны. 1 _V — вектор | В | единицы, а A _G — матрица инцидентности G , поэтому третья строка указывает на ограничение, согласно которому сумма весов вблизи каждой вершины не превышает 1. Аналогично, минимальный дробный размер вершинного покрытия в $G=(V,E)$ является решением следующей ЛП:

Минимизируйте напряжение 1 _В · у

В зависимости от: y ≥ 0 _В

__________ А _Г ^Т · у ≥ 1 _Е .

где y — вектор размера |V| в котором каждый элемент представляет вес вершины во дробном покрытии. Здесь первая строка — это размер покрытия, вторая строка — неотрицательность весов, а третья строка — требование, чтобы сумма весов возле каждого ребра была не меньше 1. Теперь минимальное дробное покрытие LP представляет собой в точности двойственную линейную программу максимального дробного соответствия LP. Следовательно, по теореме двойственности ЛП обе программы имеют одно и то же решение. Этот факт справедлив не только для двудольных, но и для произвольных графов:

В любом графе наибольший размер дробного паросочетания равен наименьшему размеру дробного вершинного покрытия.

Что делает двудольные графы особенными, так это то, что в них обе эти линейные программы имеют оптимальные решения, в которых все значения переменных являются целыми числами. Это следует из того, что в многограннике дробного совмещения двудольного графа все крайние точки имеют только целочисленные координаты, и то же самое справедливо и для многогранника дробного вершинного покрытия. Следовательно, из приведенной выше теоремы следует:

В любом двудольном графе наибольший размер паросочетания равен наименьшему размеру вершинного покрытия.

Алгоритм

Описанное выше конструктивное доказательство предоставляет алгоритм создания минимального вершинного покрытия при максимальном паросочетании. Таким образом, алгоритм Хопкрофта–Карпа для поиска максимальных паросочетаний в двудольных графах также может быть использован для эффективного решения задачи вершинного покрытия в этих графах.

Несмотря на эквивалентность двух задач с точки зрения точных решений, они не эквивалентны для аппроксимирующих алгоритмов . Двудольные максимальные паросочетания могут быть аппроксимированы сколь угодно точно за постоянное время с помощью распределенных алгоритмов ; напротив, аппроксимация минимального вершинного покрытия двудольного графа требует как минимум логарифмического времени.

Пример

На графике, показанном во введении, возьмем $L$ быть набором вершин в нижнем слое диаграммы и $R$ быть набором вершин в верхнем слое диаграммы. Слева направо пометьте вершины нижнего слоя цифрами 1, …, 7, а вершины верхнего слоя — номерами 8, …, 14. Множество $U$ несовпадающих вершин из $L$ это {1}. Переменные пути, начиная с $U$ являются 1–10–3–13–7, 1–10–3–11–5–13–7, 1–11–5–13–7, 1–11–5–10–3–13–7 и все их подпути, начиная с 1. Множество $Z$ следовательно, {1,3,5,7,10,11,13}, что приводит к $L\setminus Z=\{2,4,6\}$, $R\cap Z=\{10,11,13\}$ и минимальное вершинное покрытие $K=\{2,4,6,10,11,13\}$.

Недвудольные графы

Для графов, которые не являются двудольными, минимальное покрытие вершин может быть больше максимального соответствия. Более того, эти две задачи сильно различаются по сложности: максимальные паросочетания могут быть найдены за полиномиальное время для любого графа, а минимальное вершинное покрытие является NP-полным .

Дополнением вершинного покрытия в любом графе является независимое множество , поэтому минимальное вершинное покрытие дополняет максимальное независимое множество; нахождение максимальных независимых множеств — еще одна NP-полная задача. Эквивалентность между сопоставлением и покрытием, сформулированная в теореме Кенига, позволяет вычислять минимальные вершинные покрытия и максимальные независимые множества за полиномиальное время для двудольных графов, несмотря на NP-полноту этих проблем для более общих семейств графов.

История

Теорема Кенига названа в честь венгерского математика Денеша Кенига . Кениг объявил в 1914 году и опубликовал в 1916 году результаты о том, что каждый правильный двудольный граф имеет идеальное паросочетание . и, в более общем смысле, хроматический индекс любого двудольного графа (то есть минимальное количество паросочетаний, на которые он может быть разбит) равен его максимальной степени. – последнее утверждение известно как теорема Кенига о раскраске линий . Однако Бонди и Мурти (1976) приписывают саму теорему Кенига более поздней статье Кенига (1931).

По словам Биггса, Ллойда и Уилсона (1976) , Кениг приписал идею изучения паросочетаний в двудольных графах своему отцу, математику Дьюле Кенигу . В венгерском языке имя Кенига имеет двойной острый акцент , но его теорема иногда пишется (неправильно) немецкими буквами с умлаутом .

Связанные теоремы

Теорема Кенига эквивалентна многим другим теоремам о мин-максе в теории графов и комбинаторике, таким как теорема о браке Холла и теорема Дилворта . Поскольку двустороннее сопоставление является частным случаем максимального потока , эта теорема также вытекает из теоремы о максимальном потоке и минимальном разрезе .

Связи с идеальными графами

Граф называется совершенным , если в каждом индуцированном подграфе хроматическое число равно размеру наибольшей клики . Любой двудольный граф совершенен, потому что каждый его подграф либо двудольный, либо независимый; в двудольном графе, который не является независимым, хроматическое число и размер наибольшей клики равны двум, тогда как в независимом множестве хроматическое число и число клик равны единице.

Граф совершенен тогда и только тогда, когда его дополнение совершенно. а теорему Кенига можно рассматривать как эквивалент утверждения о том, что дополнение двудольного графа совершенно. Поскольку каждый класс цвета в раскраске дополнения двудольного графа имеет размер не более 2, а классы размера 2 образуют паросочетание, клика в дополнении графа G является независимым множеством в G , и, поскольку мы уже описали независимое множество в двудольном графе G является дополнением вершинного покрытия в G . Таким образом, любое паросочетание M в двудольном графе G с n вершинами соответствует раскраске дополнения к G с n -| М | цветов, что по совершенству дополнений к двудольным графам соответствует независимому множеству в G с n -| М | вершин, что соответствует вершинному покрытию G с M вершинами. И наоборот, теорема Кенига доказывает совершенство дополнений к двудольным графам - результат, доказанный в более явной форме Галлаем (1958) .

Теорему Кенига о раскраске линий можно также связать с другим классом совершенных графов - линейными графами двудольных графов. Если G — граф, линейный граф L ( G ) имеет вершину для каждого ребра G и ребро для каждой пары смежных ребер G. в хроматическое число L ( G ) равно хроматическому индексу G. Таким образом , Если G двудольный, клики в L ( G ) — это в точности множества ребер в G, имеющих общую конечную точку. Теперь теорема Кенига о раскраске линий, утверждающая, что хроматический индекс равен максимальной степени вершины в любом двудольном графе, можно интерпретировать как утверждение, что линейный граф двудольного графа идеален.

Поскольку линейные графы двудольных графов совершенны, дополнения к линейным графам двудольных графов также совершенны. Клика в дополнении к линейному графу G это просто паросочетание в G. — А раскраска в дополнении к линейному графу G , когда G двудольный, представляет собой разбиение ребер G на подмножества ребер, имеющих общую конечную точку; конечные точки, общие для каждого из этих подмножеств, образуют вершинное покрытие для G . Следовательно, саму теорему Кенига также можно интерпретировать как утверждение о том, что дополнения к линейным графам двудольных графов совершенны.

Взвешенные варианты

Теорему Кенига можно распространить на взвешенные графы .

. Теорема Эгервари для графов, взвешенных по ребрам

Джено Эгервари (1931) рассматривал графы, в которых каждое ребро e имеет неотрицательный целочисленный вес w _e . Весовой вектор обозначается w . W - вес паросочетания — это сумма весов ребер, участвующих в паросочетании. W - вертекс-покрытие — это мультимножество вершин («мультимножество» означает, что каждая вершина может появляться несколько раз), в котором каждое ребро e смежно как минимум с _we вершинами. Эгервари гласит: Теорема

В любом двудольном графе, взвешенном по ребрам, максимальный w- вес паросочетания равен наименьшему числу вершин в w- вершинном покрытии.

Максимальный w- вес дробного сопоставления определяется LP:

Максимизировать w · x

При условии: x ≥ 0 _E

__________ А _Г · x ≤ 1 _В .

А минимальное число вершин в дробном w- вершинном-покрытии задается двойственным ЛП:

Минимизируйте напряжение 1 _В · у

В зависимости от: y ≥ 0 _В

__________ А _Г ^Т · у ≥ ш .

Как и в доказательстве теоремы Кенига, теорема двойственности ЛП подразумевает, что оптимальные значения равны (для любого графа), а из того факта, что граф двудольный, следует, что эти программы имеют оптимальные решения, в которых все значения являются целыми числами.

Теорема для вершинно-взвешенных графов

Можно рассмотреть граф, в котором каждая вершина v имеет неотрицательный целочисленный вес b _v . Весовой вектор обозначается b . b в -вес вершинного покрытия — это сумма b _v для всех v покрытии. b v -сопоставление — это присвоение каждому ребру неотрицательного целого веса так, что сумма весов ребер, смежных с любой вершиной , не превосходит b _v . Используя аналогичный аргумент, теорему Эгервари можно распространить на графы, которые имеют как веса ребер w , так и веса вершин b :

В любом взвешенном по ребрам двудольном графе максимальный w- вес b - паросочетания равен минимальному b -весу вершин в w- вершинном покрытии.

См. также

• Собственность Кенига в гиперграфах

Ссылки

• Биггс, ЕК; Ллойд; Уилсон, Р.Дж. (1976), Теория графов 1736–1936 , Oxford University Press, стр. 203–207, ISBN  0-19-853916-9 .
• Чеза-Бьянки, Николо (11 апреля 2020 г.), Сопоставления и теорема о максимальном потоке и минимальном сокращении (PDF)
• Кук, Уильям Дж .; Каннингем, Уильям Х.; Пуллибланк, Уильям Р .; Шрийвер, Александр (2011), Комбинаторная оптимизация , Ряды Уайли по дискретной математике и оптимизации, том. 33, John Wiley & Sons, стр. 48–49, ISBN.  9781118031391 .
• Бонди, JA ; Мурти, USR (1976), Теория графов с приложениями , Северная Голландия, ISBN  0-444-19451-7 .
• Галлай, Тибор (1958), «Максимум-минимум Sätze über Graphen», Математический журнал Венгерской академии наук , 9 (3–4): 395–434, doi : 10.1007/BF02020271 , MR   0124238 .
• Гёос, Мика; Суомела, Юкка (2014), «Нет схемы аппроксимации сублогарифмического времени для двудольного вершинного покрытия», Distributed Computing , 27 (6): 435–443, arXiv : 1205.4605 , doi : 10.1007/s00446-013-0194-z , MR   3280546 , S2CID   13513566
• Кениг, Денес (1916), «Графы и их применение к теории определителей и множеств», Mathematical and Natural Science Bulletin , 34 : 104–119 .
• Кениг, Денес (1931), «Графики и матрицы», Mathematical and Physical Papers , 38 : 116–119 .
• Ловас, Ласло (1972), «Нормальные гиперграфы и гипотеза идеального графа», Discrete Mathematics , 2 (3): 253–267, doi : 10.1016/0012-365X(72)90006-4 , MR   0302480 .
• Ловас, Ласло (1974), «Теоремы о минимаксе для гиперграфов», Семинар по гиперграфам (Труды первого рабочего семестра, Университет штата Огайо, Колумбус, Огайо, 1972; посвящен Арнольду Россу) , Конспекты лекций по математике, том. 411, Берлин: Springer, стр. 111–126, номер документа : 10.1007/BFb0066186 , ISBN.  978-3-540-06846-4 , МР   0406862 .
• Ловас, Ласло ; Пламмер, доктор медицинских наук (1986), Теория соответствия , Анналы дискретной математики, том. 29, Северная Голландия, ISBN  0-444-87916-1 МР  0859549
• Сторер, Дж. А. (2001), Введение в структуры данных и алгоритмы , серия «Прогресс в области компьютерных наук и прикладной логики», Springer, ISBN  9780817642532 .