Параллелогон

В геометрии параллелогон — это многоугольник с параллельными противоположными сторонами (отсюда и название), который может путем перемещения замостить плоскость ( вращение не допускается ). ^[1]^[2]

У параллелогонов четное количество сторон и противоположные стороны, равные по длине. Менее очевидное следствие состоит в том, что параллелогоны могут иметь только четыре или шесть сторон; ^[1] на 180 градусов Параллелогоны имеют вращательную симметрию вокруг центра .

Четырехсторонний параллелогон называется параллелограммом .

Грани параллелоэдра (трехмерного аналога) называются параллелогонами. ^[2]

Два многоугольных типа

Четырехсторонние и шестиугольные параллелогоны имеют различную геометрическую симметричную форму. Все они имеют центральную инверсионную симметрию, порядок 2. Каждый выпуклый параллелогон является зоногоном , но шестиугольные параллелогоны допускают возможность создания невыпуклых многоугольников.

Стороны	Имя	Симметрия
4	Параллелограмм	Z ₂ , порядок 2
	Прямоугольник и ромб	Дих ₂ , заказ 4
	Квадрат	Дих ₄ , заказ 8
6	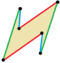удлиненный параллелограмм	Z ₂ , порядок 2
	удлиненный ромб	Дих ₂ , заказ 4
	Обычный шестиугольник	Дих ₆ , заказ 12

Геометрические вариации

Параллелограмм может замостить плоскость как искаженную квадратную мозаику , тогда как шестиугольный параллелогон может замостить плоскость как искаженную правильную шестиугольную мозаику .

Параллелограммные мозаики
1 длина		2 длины
Верно	Перекос	Верно	Перекос
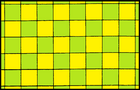Квадрат п 4 м (*442)	Ромб см (2*22)	Прямоугольник пмм (*2222)	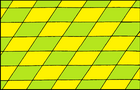Параллелограмм п 2 (2222)

Шестиугольные плитки параллелогона
1 длина	2 длины		3 длины

Правильный шестиугольник п 6 м (*632)	Вытянутый ромб см (2*22)		Вытянутый параллелограмм п 2 (2222)

Ссылки

^ Jump up to: Перейти обратно: ^а ^б Aleksandr Danilovich Alexandrov (2005) [1950]. Convex Polyhedra . Translated by N.S. Dairbekov; S.S. Kutateladze; A.B. Sosinsky. Springer. p. 351 . ISBN 3-540-23158-7 . ISSN 1439-7382 .
^ Jump up to: Перейти обратно: ^а ^б Грюнбаум, Бранко (01 декабря 2010 г.). «Додекаэдр Билинского и различные параллелоэдры, зоноэдры, моноэдры, изозоноэдры и другие эдры» . Математический интеллект . 32 (4): 5–15. дои : 10.1007/s00283-010-9138-7 . hdl : 1773/15593 . ISSN 1866-7414 . S2CID 120403108 . PDF

Факты в досье: Справочник по геометрии , Кэтрин А. Горини, 2003 г., ISBN 0-8160-4875-4 , с. 117
Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 0-7167-1193-1 . список 107 изоэдральных мозаик, с. 473-481

Внешние ссылки

Пять параллелоэдров Федорова.

[aleksandrov-1] Jump up to: Перейти обратно: ^а ^б Aleksandr Danilovich Alexandrov (2005) [1950]. Convex Polyhedra . Translated by N.S. Dairbekov; S.S. Kutateladze; A.B. Sosinsky. Springer. p. 351 . ISBN 3-540-23158-7 . ISSN 1439-7382 .

[Grünbaum-2] Jump up to: Перейти обратно: ^а ^б Грюнбаум, Бранко (01 декабря 2010 г.). «Додекаэдр Билинского и различные параллелоэдры, зоноэдры, моноэдры, изозоноэдры и другие эдры» . Математический интеллект . 32 (4): 5–15. дои : 10.1007/s00283-010-9138-7 . hdl : 1773/15593 . ISSN 1866-7414 . S2CID 120403108 . PDF

[1]

[2]