Роза (математика)

Розы, указанные синусоидом $r = cos (kθ)$ для различных рациональных нумерованных значений угловой частоты $k = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ n / d ⁠$ .
Розы, указанные $R = sin (kθ),$ представляют собой вращения этих роз на четверть периода синусоида в направлении против часовой стрелки вокруг полюса (происхождение). Для надлежащего математического анализа $K$ должен быть выражен в непревзойденной форме.

В математике кривая розовой или родонеи представляет собой синусоид , указанный либо косинусами , либо синусоидальными функциями без фазового угла , который построен в полярных координатах . Кривые розы или «родонея» были названы итальянским математиком, который изучал их, Гвидо Гранди , между 1723 и 1728 годами. ^{[ 1 ]}

Общий обзор

Спецификация

Роза - это набор точек в полярных координатах, указанных полярным уравнением ^{[ 2 ]}

r=a\cos(k\theta )

или в декартовых координатах с использованием параметрических уравнений

{\begin{aligned}x&=r\cos(\theta )=a\cos(k\theta )\cos(\theta )\\y&=r\sin(\theta )=a\cos(k\theta )\sin(\theta )\end{aligned}}

Розы также могут быть указаны с использованием функции синуса. ^{[ 3 ]} С

\sin(k\theta )=\cos \left(k\theta -{\frac {\pi }{2}}\right)=\cos \left(k\left(\theta -{\frac {\pi }{2k}}\right)\right)

.

Таким образом, роза, указанная $r = a sin (kθ)$ , идентична той, которая указана $r = a cos (kθ)$ вращается против часовой стрелки на $⁠ π / 2 K ⁠$ Радины, которые составляют четверть период любого синусоида.

Поскольку они указаны с использованием функции косинуса или синуса, розы обычно выражаются в виде полярных координат (а не декартовых координат ) графиков синусоидов, которые имеют угловую частоту K $и$ амплитуду A , $угла$ которые определяют радиальную координату $R,$ с учетом полярного $θ$ ( Хотя, когда $K$ является рациональным числом , кривая розы может быть выражена в картезианских координатах, поскольку они могут быть указаны как алгебраические кривые ^{[ 4 ]}).

Общие свойства

Художественное описание роз с различными настройками параметров

Розы напрямую связаны со свойствами синусоидов, которые их указывают.

Лепестки

Графики роз состоят из лепестков . Лепесток-это форма, образованная графиком полуцикла синусоида, который указывает розу. (Цикл - это часть синусоида, которая составляет один период t = ⁠ 2 π / k ⁠ длиной и состоит из положительного полуцикла, непрерывного набора точек, где r ≥ 0 и ⁠ T / 2 ⁠ = ⁠ π / k ⁠ длиной, а отрицательный полуцикл-это другая половина, где r ≤ 0. )
- Форма каждого лепестка одинакова, потому что графики полуцикла имеют одинаковую форму. Форма определяется положительным полуциком с гребнем при $(a, 0),$ указанный как $r = a cos (kθ)$ (который ограничен интервалом $угла- ⁠ T / 4 ⁠ \leq θ \leq ⁠ T / 4 ⁠$ ). Лепесток симметричен в отношении полярной оси. Все остальные лепестки являются вращениями указанных синусоидальной функцией с теми же значениями для $A$ и $K.$ этого лепестка о полюсе, в том числе для роз , ^{[ 5 ]}
- В соответствии с правилами построения точек на полярных координатах, точка в отрицательном полуциклом не может быть построена под его полярным углом, поскольку ее радиальная координата $R$ является отрицательной. Точка построена путем добавления $π$ -радиан в полярный угол с радиальной координатой $| r |$ Полем Таким образом, положительные и отрицательные полуциклы могут быть совпадают с графиком розы. Кроме того, розы вписаны в круг $r = a$ .
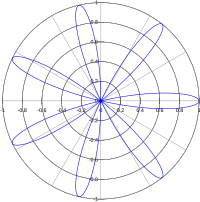
- Когда период $t$ синусоида меньше или равен $4 π$ , форма лепестка представляет собой единый закрытый цикл. Один цикл образуется, потому что угловой интервал для полярного графика составляет $2 π$ , а угловая ширина полуцикла меньше или равна $2 π$ . Когда $t > 4 π$ (или $| k | < ⁠ 1/2 один образует ⁠$ ) График полупроката можно рассматривать как выпивший из полюса более чем в одной цепь вокруг полюса, пока график не достигнет вписанного круга, где он списается обратно на полюс, пересекает себя и Больше петель по пути. Следовательно, каждый лепесток образует две петли, когда $4 π < t \leq 8 π$ (или $⁠ 1/4 ⁠ \leq | K | < ⁠ 1/2 8 ⁠)$ , три петли, когда $π < t \leq 12 π$ (или $⁠ 1/6 ⁠ \leq | K | < ⁠ 1/4 и т . ⁠)$ Д. Розы с одним лепестой с несколькими петлями наблюдаются для $k = ⁠ 1 / 3 ⁠, ⁠ 1 / 5 ⁠, ⁠ 1/7 и т . Д. (⁠$ См. Рисунок в разделе «Введение».)
- Лепестки розы не будут пересекаться друг с другом, когда угловая частота $k$ является ненулевым целым числом; В противном случае лепестки пересекают друг друга.

Симметрия

Все розы отображают одну или несколько форм симметрии из -за основных симметричных и периодических свойств синусоидов.

Роза, указанная как $r = a cos (kθ)$ , симметрична относительно полярной оси (линия $θ = 0$ ) из -за идентичности a $cos (kθ) = a cos ( - kθ)$ , что указывает розы, указанные двумя полярными уравнениями совпадающий.

Роза, указанная как $r = a sin (kθ)$ , симметрична относительно вертикальной линии $θ = ⁠ π / 2 ⁠$ Из -за идентичности $a sin (kθ) = a sin (π - kθ)$ , что делает розы, указанные двумя полярными уравнениями, совпадают.

Только определенные розы симметричны по поводу полюса.

Отдельные лепестки симметричны по поводу линии через полюс и пик лепестки, который отражает симметрию полуцикла базового синусоида. Розы, состоящие из конечного числа лепесток, по определению, вращательно симметричны, так как каждый лепесток - одна и та же форма с последовательными лепестками, вращающимися под тем же углом вокруг полюса.

Розы с ненулевыми целочисленными значениями $k$

Когда $k$ является ненулевым целым числом, кривая будет в форме розы с $2 К$ лепесткам, если $k$ ровно, и $k$ лепестки, когда $k$ нечетно. ^{[ 6 ]} Свойства этих роз являются особым случаем роз с угловыми частотами $k$ , которые являются рациональными числами, обсуждаемыми в следующем разделе этой статьи.

Роза вписана в круг $r = a$ , соответствующую радиальной координате всех его пиков.

Поскольку полярный координатный график ограничен полярными углами между 0 и $2 π$ , есть $⁠ 2 π / T ⁠ = K$ Циклы, отображаемые на графике. Никакие дополнительные точки не должны быть нанесены на график, потому что радиальная координата при $θ = 0$ является одинаковым значением при $θ = 2 π$ (которые являются гребнями для двух разных положительных полупрозрачных циклов для роз, указанных функцией косинуса).

Когда k равно (и ненулевой), роза состоит из 2 К- лепесток, по одному для каждого пика в 2 π- интервале отображаемых полярных углов. Каждый пик соответствует точке, лежащей на круге r = a . Линейные сегменты, соединяющие последовательные пики, образуют обычный многоугольник с равномерным количеством вершин, которые имеют центр на полюсе и радиус через каждый пик, а также:
- Розы симметричны по поводу полюса.
- Розы симметричны вокруг каждой линии через полюс и пик (через «средний» лепесток) с полярным углом между пиками последовательных лепестков $⁠ 2 π / 2 k ⁠ = ⁠ π / k ⁠$ Радины. Таким образом, эти розы имеют вращательную симметрию порядка $2 к$ .
- Розы симметричны в отношении каждой линии, которая разделяет угол между последовательными пиками, что соответствует границам полуцикла и апотема соответствующего многоугольника.

Когда k нечетная, роза состоит из лепестков K , по одному для каждого гребня (или впадины) в 2 π -интервале отображаемых полярных углов. Каждый пик соответствует точке, лежащей на круге r = a . Эти положительные и отрицательные полуциклы этой розы совпадают, что означает, что при графике их, только положительные полуциклы или только отрицательные полупрозрачные циклы должны нанести на график, чтобы сформировать полную кривую. (Эквивалентно, полная кривая будет графичена путем построения любого непрерывного интервала полярных углов, которые являются π -радианами, такими как θ = 0 до θ = π . ^{[ 7 ]}) Сегменты линий, соединяющие последовательные пики, образуют обычный многоугольник с нечетным количеством вершин, а также:
- Розы симметричны вокруг каждой линии через полюс и пик (через середину лепестки) с полярным углом между пиками последовательных лепестков. $⁠ 2 π / k ⁠$ Радины. Таким образом, эти розы имеют вращательную симметрию порядка $k$ .

Лепестки розы не перекрываются.

Розы могут быть указаны с помощью алгебраических кривых порядка $k + 1,$ когда $k$ нечетный, и $2 (k + 1)$ , когда $k$ ровно. ^{[ 8 ]}

Круг

Роза с $k = 1$ - это круг , который лежит на полюсе диаметром, который лежит на полярной оси, когда $r = a cos (θ)$ . Круг - это одиночный лепесток кривой. (См. Круг, образованный в конце следующего раздела.) В координатах декартовых изделий эквивалентные спецификации косинуса и синуса

\left(x-{\frac {a}{2}}\right)^{2}+y^{2}=\left({\frac {a}{2}}\right)^{2}

и

x^{2}+\left(y-{\frac {a}{2}}\right)^{2}=\left({\frac {a}{2}}\right)^{2}

соответственно.

Квадрофиум

Роза с $k = 2$ называется квадволием , потому что она имеет $2k = 4$ лепестки и будет образовывать квадрат . В координатах декартовых характеристик и косинус и синусоидальные характеристики

\left(x^{2}+y^{2}\right)^{3}=a^{2}\left(x^{2}-y^{2}\right)^{2}

и

\left(x^{2}+y^{2}\right)^{3}=4\left(axy\right)^{2}

соответственно.

Трифолиум

Роза с $k = 3$ называется Trifolium ^{[ 9 ]} потому что он имеет $k = 3$ лепестки и будет сформировать равносторонний треугольник . Кривая также называется Paquerette de Mélibée. В координатах декартовых характеристик и косинус и синусоидальные характеристики

\left(x^{2}+y^{2}\right)^{2}=a\left(x^{3}-3xy^{2}\right)

и

\left(x^{2}+y^{2}\right)^{2}=a\left(3x^{2}y-y^{3}\right)

соответственно. ^{[ 10 ]} (См. Трифолиум, образованный в конце следующего раздела.)

Октафолиум

Роза с $k = 4$ называется октафолием , потому что она имеет $2K = 8$ лепестков и будет образовывать восьмиугольник . В координатах декартовых характеристик и косинус и синусоидальные характеристики

\left(x^{2}+y^{2}\right)^{5}=a^{2}\left(x^{4}-6x^{2}y^{2}+y^{4}\right)^{2}

и

\left(x^{2}+y^{2}\right)^{5}=16a^{2}\left(xy^{3}-yx^{3}\right)^{2}

соответственно.

Пентафолий

Роза с $k = 5$ называется пентафолием , потому что у нее есть $k = 5$ лепестков и образует обычный Пентагон . В координатах декартовых характеристик и синусоидальные спецификации

\left(x^{2}+y^{2}\right)^{3}=a\left(x^{5}-10x^{3}y^{2}+5xy^{4}\right)

и

\left(x^{2}+y^{2}\right)^{3}=a\left(5x^{4}y-10x^{2}y^{3}+y^{5}\right)

соответственно.

Додекафолиум

Роза с $k = 6$ называется додекафолием , потому что она имеет $2k = 12$ лепестков и будет образовывать додекагона . В координатах декартовых характеристик и косинус и синусоидальные характеристики

\left(x^{2}+y^{2}\right)^{7}=a^{2}\left(x^{6}-15x^{4}y^{2}+15x^{2}y^{4}-y^{6}\right)^{2}

и

\left(x^{2}+y^{2}\right)^{7}=4a^{2}\left(3x^{5}y-10x^{3}y^{3}+3xy^{5}\right)^{2}

соответственно.

Общее и лепестки

Общая площадь розы с полярным уравнением формы $r = a cos (kθ)$ или $r = a sin (kθ)$ , где $k$ -ненулевое целое число, есть ^{[ 11 ]}

{\begin{aligned}{\frac {1}{2}}\int _{0}^{2\pi }(a\cos(k\theta ))^{2}\,d\theta &={\frac {a^{2}}{2}}\left(\pi +{\frac {\sin(4k\pi )}{4k}}\right)={\frac {\pi a^{2}}{2}}&&\quad {\text{for even }}k\\[8px]{\frac {1}{2}}\int _{0}^{\pi }(a\cos(k\theta ))^{2}\,d\theta &={\frac {a^{2}}{2}}\left({\frac {\pi }{2}}+{\frac {\sin(2k\pi )}{4k}}\right)={\frac {\pi a^{2}}{4}}&&\quad {\text{for odd }}k\end{aligned}}

Когда $k$ evely, есть $2 К$ -лепестки; и когда $k$ станет странным, есть $k$ лепестки, поэтому область каждого лепестка $⁠ πa 2 / 4 k ⁠$ .

Розы с рациональными значениями для $k$

В общем, когда $k$ является рациональным числом в неокращенной форме $фракции k = ⁠ N / D ⁠$ , где $N$ и $D$ являются ненулевыми целыми числами, количество лепестков является знаменателем выражения $⁠ 1 / 2 ⁠ - ⁠ 1 / 2 k ⁠ = ⁠ N - D / 2 N ⁠$ . ^{[ 12 ]} Это означает, что количество лепестков составляет $n$ , если как $N,$ так и $D$ нечетные, а $2 n$ в противном случае. ^{[ 13 ]}

В случае, когда как $N$ , так и $D$ являются нечетными, положительные и отрицательные полуциклы синусоидов совпадают. График этих роз завершается в любом непрерывном интервале полярных углов, $длиной Dπ$ . ^{[ 14 ]}

Когда n ровно и d нечетная или виза, роза будет полностью графична в непрерывном интервале полярного угла длиной 2 dπ . ^{[ 15 ]} Кроме того, розы симметричны в отношении полюса как для технических характеристик косинуса, так и для синусоидальных характеристик. ^{[ 16 ]}
- Кроме того, когда $n$ нечетный, а $D$ - ровный, розы, указанные косинусными и синусоидальными полярными уравнениями с одинаковыми значениями $A$ и $K,$ совпадают. Для такой пары роз роза со спецификацией функции синуса совпадает с гребнем розы со спецификацией косинуса на полярной оси либо при $θ = ⁠ dπ / 2 ⁠$ или при $θ = ⁠ 3 dπ / 2 ⁠$ . (Это означает, что розы $r = a cos (kθ)$ и $r = a sin (kθ)$ с ненулевыми целочисленными значениями $k$ никогда не совпадают.)

Роза вписана в круг $r = a$ , соответствующую радиальной координате всех его пиков.

Дюрер Фолиум

Роза с $k = ⁠ 1/2 Дюрера гравера ⁠$ называется Дюрером Фолимом, названным в честь немецкого художника и Альбрехта . Розы, указанные $R = A COS (⁠ θ / 2 ⁠)$ и $r = a sin (⁠ θ / 2 ⁠)$ совпадают, хотя $COS (⁠ θ / 2 ⁠) \neq грех (⁠ θ / 2 ⁠)$ . В картезианских координатах роза указана как ^{[ 17 ]}

\left(x^{2}+y^{2}\right)\left(2\left(x^{2}+y^{2}\right)-a^{2}\right)^{2}=a^{4}x^{2}

Дюрер Фолиум также является трисектриксом , кривой, которую можно использовать для углах трисекта.

Limaçon Trisectrix

Роза с $k = ⁠ 1/3 -, ⁠$ это TriSectrix Limaçon которая имеет свойство кривых Trisectrix , которые можно использовать для углах трисекта. Роза имеет один лепесток с двумя петлями. (См. Анимацию ниже.)

Примеры роз

r = cos (kθ),

созданные с использованием передач с различными соотношениями.
Отображаемые лучи представляют собой полярную ось и

θ = ⁠ π / 2 ⁠

.
График начинается с

θ = 2 π,

когда

k

является целым числом,

θ = 2 dπ

в противном случае и перемещается по часовой стрелке до

θ = 0

.

Круг = ,

k = 1

(

n = 1

,

d 1

). Роза завершена, когда

θ = π

достигается (половина революции более легкой передачи).

The Limaçon trisectrix ,

k = ⁠ 1/3) n ⁠

(

, = 1

d

= 3

, имеет один лепесток с двумя петлями. Роза завершена, когда

θ = 3 π

достигнута ( ⁠ 3/2 ) ⁠ Революции более легкой передачи

Трифолия,

k = 3

(

n = 3

,

d = 1

). Роза завершена, когда

θ = π

достигается (половина революции более легкой передачи).

8 лепестков розы с

k = ⁠ 4/5) - n ⁠

(

= 4

,

D = 5

это один цикл, который пересекает другие лепестки. Роза симметрична по поводу полюса. Роза завершена при

θ = 10 π

(пять революций более легкой передачи).

Розы с иррациональными значениями для $k$

Кривая розы, указанная с иррациональным числом для $K,$ имеет бесконечное количество лепестков ^{[ 18 ]} и никогда не будет завершено. Например, синусоид $r = a cos (πθ)$ имеет период $t = 2$ , поэтому он имеет лепесток в интервале полярного угла $- ⁠ 1/2 2 ⁠ \leq θ \leq ⁠ 1/2; оси ⁠$ с гребнем на полярной Однако в домене полярного уравнения нет другого полярного угла, который будет построен в координатах $(A, 0)$ . В целом, розы, указанные синусоидами с угловыми частотами, которые являются иррациональными константами, образуют плотный набор (то есть они произвольно близки к указанию каждой точки на диске $R \leq a$ ).

Смотрите также

Limaçon Trisectrix - имеет такую же форму, что и роза с $k = ⁠ 1 / 3 ⁠$ .
Quadrifolium - кривая розы, где $k = 2$ .
Маурер Роуз
Роза (топология)
Sectrix of Maclaurin
Спирограф

Примечания

^ О'Коннор, Джон Дж.; Робертсон , , MacTutor History of Mathematics Archive, Родонея
^ Математические модели Х. Мартина Кунди и AP Rollett, второе издание, 1961 (издательство Оксфордского университета), с. 73.
^ «Роза (математика)» . Получено 2021-02-02 .
^ Роберт Ферреол. "Роза" . Получено 2021-02-03 .
^ XAH LEE. "Кривая розы" . Получено 2021-02-12 .
^ Эрик В. Вайсштейн. «Роза (математика)» . Wolfram Mathworld . Получено 2021-02-05 .
^ «Количество лепестков нечетной кривой rodonea» . Presesswiki.org . Получено 2021-02-03 .
^ Роберт Ферреол. "Роза" . Получено 2021-02-03 .
^ «Трифолиум» . Получено 2021-02-02 .
^ Эрик В. Вайсштейн. "Paquerette de Mélibée" . Wolfram Mathworld . Получено 2021-02-05 .
^ Роберт Ферреол. "Роза" . Получено 2021-02-03 .
^ Ян Вассенаар. «Родонея» . Получено 2021-02-02 .
^ Роберт Ферреол. "Роза" . Получено 2021-02-05 .
^ XAH LEE. "Кривая розы" . Получено 2021-02-12 .
^ XAH LEE. "Кривая розы" . Получено 2021-02-12 .
^ Ян Вассенаар. «Родонея» . Получено 2021-02-02 .
^ Роберт Ферреол. «Дюрер Фолиум» . Получено 2021-02-03 .
^ Эрик В. Вайсштейн. «Роза (математика)» . Wolfram Mathworld . Получено 2021-02-05 .

Внешние ссылки

Апплет для создания Rose с $k$ параметром
Визуальный словарь специальных кривых самолетов Xah Lee
Интерактивный пример с JSXGRAPH
Создайте кривую розы в качестве векторной графики (с помощью синусоидальной функции)

[1] О'Коннор, Джон Дж.; Робертсон , , MacTutor History of Mathematics Archive, Родонея

[2] Математические модели Х. Мартина Кунди и AP Rollett, второе издание, 1961 (издательство Оксфордского университета), с. 73.

[3] «Роза (математика)» . Получено 2021-02-02 .

[4] Роберт Ферреол. "Роза" . Получено 2021-02-03 .

[5] XAH LEE. "Кривая розы" . Получено 2021-02-12 .

[6] Эрик В. Вайсштейн. «Роза (математика)» . Wolfram Mathworld . Получено 2021-02-05 .

[7] «Количество лепестков нечетной кривой rodonea» . Presesswiki.org . Получено 2021-02-03 .

[8] Роберт Ферреол. "Роза" . Получено 2021-02-03 .

[9] «Трифолиум» . Получено 2021-02-02 .

[10] Эрик В. Вайсштейн. "Paquerette de Mélibée" . Wolfram Mathworld . Получено 2021-02-05 .

[11] Роберт Ферреол. "Роза" . Получено 2021-02-03 .

[12] Ян Вассенаар. «Родонея» . Получено 2021-02-02 .

[13] Роберт Ферреол. "Роза" . Получено 2021-02-05 .

[14] XAH LEE. "Кривая розы" . Получено 2021-02-12 .

[15] XAH LEE. "Кривая розы" . Получено 2021-02-12 .

[16] Ян Вассенаар. «Родонея» . Получено 2021-02-02 .

[17] Роберт Ферреол. «Дюрер Фолиум» . Получено 2021-02-03 .

[18] Эрик В. Вайсштейн. «Роза (математика)» . Wolfram Mathworld . Получено 2021-02-05 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

Общий обзор

Спецификация

Общие свойства

Лепестки

Симметрия

Розы с ненулевыми целочисленными значениями k

Круг

Квадрофиум

Трифолиум

Октафолиум

Пентафолий

Додекафолиум

Общее и лепестки

Розы с рациональными значениями для k

Дюрер Фолиум

Limaçon Trisectrix

Розы с иррациональными значениями для k

Смотрите также

Примечания

Внешние ссылки

Розы с ненулевыми целочисленными значениями $k$

Розы с рациональными значениями для $k$

Розы с иррациональными значениями для $k$