Скорость выделения энергии (механика разрушения)

В механике разрушения скорость энерговыделения , $G$ представляет собой скорость, с энергия преобразуется которой при материала разрушении . , Математически скорость выделения энергии выражается как уменьшение полной потенциальной энергии при увеличении площади поверхности разрушения: и, таким образом, выражается в единицах энергии на единицу площади. Могут быть построены различные энергетические балансы, связывающие энергию, выделяющуюся при разрушении, с энергией образующейся новой поверхности, а также с другими диссипативными процессами, такими как пластичность и тепловыделение. Скорость выделения энергии занимает центральное место в области механики разрушения при решении задач и оценке свойств материала, связанных с разрушением и усталостью .

Определение

График зависимости нагрузки от смещения

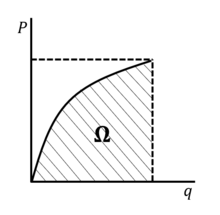
Скорость выделения энергии $G$ определяется как мгновенная потеря полной потенциальной энергии $\Pi$ на единицу площади роста трещины $s$,

$G\equiv -{\frac {\partial \Pi }{\partial s}},$

где полная потенциальная энергия выражается через полную энергию деформации $\Omega$, поверхностное сцепление $\mathbf {t}$, смещение $\mathbf {u}$и объемная сила $\mathbf {b}$ к

$\Pi =\Omega -\left\{\int _{{\mathcal {S}}_{t}}\mathbf {t} \cdot \mathbf {u} \,dS+\int _{\mathcal {V}}\mathbf {b} \cdot \mathbf {u} \,dV\right\}.$

Первый интеграл находится по поверхности $S_{t}$ материала, а второй – по его объему $V$.

На рисунке справа показан график внешней силы. $P$ в зависимости от смещения точки нагрузки $q$, где площадь под кривой представляет собой энергию деформации. Белая область между кривой и $P$-ось называется дополнительной энергией. В случае линейно-упругого материала $P(q)$ представляет собой прямую линию, а энергия деформации равна дополнительной энергии.

Предписанное смещение

В случае заданного смещения энергия деформации может быть выражена через заданное перемещение и поверхность трещины. $\Omega (q,s)$, а на изменение этой энергии деформации влияет только изменение площади поверхности разрушения: $\delta \Omega =(\partial \Omega /\partial s)\delta s$. Соответственно, скорость энерговыделения в этом случае выражается как

$G=-\left.{\frac {\partial \Omega }{\partial s}}\right|_{q}.$

Вот здесь можно точно сослаться на $G$ как скорость выделения энергии деформации.

Предписанные нагрузки

Когда вместо смещения задана нагрузка, энергию деформации необходимо изменить как $\Omega (q(P,s),s)$. Затем скорость выделения энергии рассчитывается как

$G=-\left.{\frac {\partial }{\partial s}}\right|_{P}\left(\Omega -Pq\right).$

Если материал линейно-упругий, то $\Omega =Pq/2$ и вместо этого можно написать

$G=\left.{\frac {\partial \Omega }{\partial s}}\right|_{P}.$

G в двумерных случаях

В случае двумерных задач изменение площади роста трещины представляет собой просто изменение длины трещины, умноженной на толщину образца. А именно, $\partial s=B\partial a$. Следовательно, уравнение для вычисления $G$ можно изменить для 2D-случай:

• Предписанное смещение: $G=-\left.{\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}\right|_{q}.$
• Предписанная нагрузка: $G=-\left.{\frac {1}{B}}{\frac {\partial }{\partial a}}\right|_{P}\left(\Omega -Pq\right).$
• Предписанная нагрузка, линейная упругость: $G=\left.{\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}\right|_{P}.$

Для получения дополнительной информации можно обратиться к примерам вычислений, приведенным в следующем разделе. Иногда энергию деформации записывают через $U=\Omega /B$, энергия на единицу толщины. Это дает

• Предписанное смещение: $G=-\left.{\frac {\partial U}{\partial a}}\right|_{q}.$
• Предписанная нагрузка: $G=-\left.{\frac {\partial }{\partial a}}\right|_{P}\left(U-{\frac {Pq}{B}}\right).$
• Предписанная нагрузка, линейная упругость: $G=\left.{\frac {\partial U}{\partial a}}\right|_{P}.$

Связь с факторами интенсивности стресса

Скорость выделения энергии напрямую связана с коэффициентом интенсивности напряжений , связанным с данным двумерным режимом нагружения ( режим I, режим II или режим III ), когда трещина растет прямо вперед. Это применимо к трещинам под действием плоского напряжения , плоской деформации и антиплоского сдвига .

Для режима I скорость выделения энергии $G$ Скорость связана с коэффициентом интенсивности стресса режима I. $K_{I}$ для линейно-упругого материала по

$G={\frac {K_{I}^{2}}{E'}},$

где $E'$ связано с модулем Юнга $E$ и коэффициент Пуассона $\nu$ в зависимости от того, находится ли материал под плоским напряжением или плоской деформацией:

$E'={\begin{cases}E,&\mathrm {plane~stress} ,\\\\{\dfrac {E}{1-\nu ^{2}}},&\mathrm {plane~strain} .\end{cases}}$

Для режима II скорость выделения энергии аналогично записывается как

$G={\frac {K_{II}^{2}}{E'}}.$

Для режима III (антиплоский сдвиг) скорость энерговыделения теперь является функцией модуля сдвига. $\mu$,

$G={\frac {K_{III}^{2}}{2\mu }}.$

Для произвольной комбинации всех режимов нагружения эти линейно-упругие решения можно совместить как

$G={\frac {K_{I}^{2}}{E'}}+{\frac {K_{II}^{2}}{E'}}+{\frac {K_{III}^{2}}{2\mu }}.$

showАльтернативное представление $G$ с точки зрения $K$
$G={\begin{cases}{\frac {(1-\nu )^{2}}{E}}(K_{I}^{2}+K_{II}^{2})+(1-\nu )K_{III}^{2}&{\text{plane strain}}\\{\frac {1}{E}}(K_{I}^{2}+K_{II}^{2})&{\text{plane stress}}\end{cases}}$ Which can be seen to be equivalent to the previous representation through the relationship between Young's modulus and the shear modulus: $E=2G(1+\nu )$

Связь с вязкостью разрушения

Рост трещины начинается, когда скорость энерговыделения превышает критическое значение. $G_{c}$, которое является материальным свойством,

$G\geq G_{c},$

При нагрузке режима I критическая скорость выделения энергии $G_{c}$ в режиме I. тогда это связано с вязкостью разрушения $K_{IC}$, другое материальное свойство, по

$G_{c}={\frac {K_{IC}^{2}}{E'}}.$

Вычисление G

Существует множество методов расчета скорости энерговыделения с учетом свойств материала, геометрии образца и условий нагрузки. Некоторые из них зависят от соблюдения определенных критериев, например, от того, что материал полностью эластичен или даже линейно-эластичен, и/или что трещина должна расти прямо вперед. Единственный представленный метод, работающий произвольно, — это использование полной потенциальной энергии. Если оба метода применимы, они должны давать одинаковые скорости выделения энергии.

Полная потенциальная энергия

Единственный метод расчета $G$ для произвольных условий заключается в вычислении полной потенциальной энергии и дифференцировании ее по площади поверхности трещины. Обычно это делается:

• расчет поля напряжений, возникающего в результате нагружения,
• расчет энергии деформации материала, возникающей в результате поля напряжений,
• расчет работы, совершаемой внешними нагрузками,

все с точки зрения площади поверхности трещины.

showПример расчета $G$ используя полную потенциальную энергию

Double cantilever beam (DCB) specimen under tensile load. This problem is two-dimensional and has a fixed load, so with $s=aB$, $G=-{\frac {1}{B}}\left.{\frac {\partial }{\partial a}}\right|_{P}(\Omega -Pq).$ Since the material is linearly-elastic, $\Omega =Pq/2$ and thus $G={\frac {1}{B}}{\frac {\partial \Omega }{\partial a}}.$ The stresses in the DCB are due to the bending stresses in each cantilever beam, $\sigma _{11}(x,y)=-{\frac {M(x)y}{I}}=-{\frac {12Pxy}{Bh^{3}}},$ where $B$ is the length into the page. Using $W=\sigma _{11}^{2}/2E$, one now has the strain energy $\Omega =\int _{V}W\,dV=2B\int _{-h/2}^{h/2}\int _{0}^{a}{\frac {1}{2E}}\left({\frac {12Pxy}{Bh^{3}}}\right)^{2}\,dx\,dy,$ where the factor of 2 out front is due to there being 2 cantilever beams. Solving, $\Omega ={\frac {P^{2}}{B^{3}}}{\frac {4a^{3}}{Eh^{3}}},$ then taking a derivative with respect to $a$ and dividing by $B$, $G={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.$

Метод соответствия

Если материал линейно упругий, расчет скорости его энерговыделения может быть значительно упрощен. В этом случае кривая зависимости нагрузки от смещения точки нагрузки является линейной с положительным наклоном, а смещение на единицу приложенной силы определяется как податливость, $C$

$C={\frac {q}{P}}.$

Соответствующая энергия деформации $\Omega$ (площадь под кривой) равна

$\Omega ={\frac {1}{2}}Pq={\frac {1}{2}}{\frac {q^{2}}{C}}={\frac {1}{2}}P^{2}C.$

Используя метод податливости, можно показать, что скорость энерговыделения для обоих случаев заданной нагрузки и перемещения оказывается равной

$G={\frac {1}{2}}P^{2}{\frac {\partial C}{\partial s}}.$

showПример расчета $G$ используя метод соответствия

A Double Cantilever Beam Specimen with Thickness B (not shown) Consider a double cantilever beam (DCB) specimen as shown in the right figure. The displacement of a single beam is $\nu _{max}={\frac {Pa^{3}}{3EI}},\quad {\text{with}}\quad I={\frac {Bh^{3}}{12}}.$ The resulting load-point displacement $q$ is therefore $2\nu _{max}$. Substitute into the equation for compliance and simplify: $C={\frac {q}{P}}={\frac {8a^{3}}{EBh^{3}}}.$ Now, ${\partial C}/{\partial s}$ is computed as ${\frac {\partial C}{\partial s}}={\frac {\partial C}{\partial a}}{\frac {\partial a}{\partial s}}=\left({\frac {24a^{2}}{EBh^{3}}}\right)\left({\frac {1}{B}}\right).$ Finally, the energy release rate of this DCB specimen can be expressed as $G(P,a)={\frac {1}{2}}P^{2}{\frac {\partial C}{\partial s}}={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.$ Note that alternatively, the energy release rate can be expressed in terms of $q$ and $a$: $G(q,a)={\frac {3}{16}}{\frac {Eh^{3}q^{2}}{a^{4}}},$ indicating that $G$ decreases with the crack length $a$ for the case of fixed displacement, and vice versa for the case of fixed load.

Методы использования нескольких образцов для нелинейных материалов

Графическое изображение G в условиях фиксированного смещения и фиксированной нагрузки

В случае заданного смещения, при фиксированной длине трещины, скорость энерговыделения можно вычислить по формуле

$G=-\int _{0}^{q}{\frac {\partial P}{\partial s}}\,dq,$

в то время как в случае предписанной нагрузки

$G=\int _{0}^{P}{\frac {\partial q}{\partial s}}\,dP.$

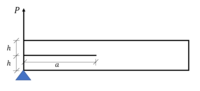
Как видно, в обоих случаях скорость энерговыделения $G$ раз больше изменения поверхности $ds$ возвращает площадь между кривыми, которая указывает энергию, рассеиваемую на новой площади поверхности, как показано на рисунке справа.

$Gds=-ds\int _{0}^{q}{\frac {\partial P}{\partial s}}\,dq=ds\int _{0}^{P}{\frac {\partial q}{\partial s}}\,dP.$

Интегральное закрытие трещины

Поскольку скорость энерговыделения определяется как отрицательная производная полной потенциальной энергии по отношению к росту поверхности трещины, скорость энерговыделения можно записать как разность между потенциальной энергией до и после роста трещины. После некоторых тщательных выводов это приводит к интегралу закрытия трещины

$G=\lim _{\Delta s\to 0}-{\frac {1}{\Delta s}}\int _{\Delta s}{\frac {1}{2}}\,t_{i}^{0}\left(\Delta u_{i}^{+}-\Delta u_{i}^{-}\right)\,dS,$

где $\Delta s$ – новая площадь поверхности разрушения, $t_{i}^{0}$ – компоненты силы сцепления, возникающей на верхней поверхности излома по мере роста трещины, $\Delta u_{i}^{+}-\Delta u_{i}^{-}$ – компоненты смещения раскрытия трещины (разница в шагах смещения между верхней и нижней поверхностями трещины), а интеграл – по поверхности материала $S$.

Интеграл закрытия трещины справедлив только для упругих материалов, но справедлив и для трещин, растущих в любом направлении. Тем не менее, для двумерной трещины, которая действительно растет прямо вперед, интеграл закрытия трещины упрощается до

$G=\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\int _{0}^{\Delta a}\sigma _{i2}(x_{1},0)u_{i}(\Delta a-x_{1},\pi )\,dx_{1},$

где $\Delta a$ – новая длина трещины, а компоненты смещения записаны как функция полярных координат $r=\Delta a-x_{1}$ и $\theta =\pi$.

showПример расчета $G$ используя интеграл закрытия трещины

Double cantilever beam (DCB) specimen under tensile load. Consider the crack in the DCB specimen shown in the figure. The nonzero stress and displacement components are given by as $\sigma _{22}(x_{1},0)={\frac {K_{I}}{\sqrt {2\pi x_{1}}}},\qquad u_{22}(\Delta a-x_{1},\pi )={\frac {8K_{I}}{E}}{\sqrt {\frac {\Delta a_{1}-x_{1}}{2\pi }}}.$ The crack closure integral for this linearly elastic material, assuming the crack grows straight ahead, is $G={\frac {2K_{I}^{2}}{\pi E}}\,\lim _{\Delta a\to 0}{\frac {1}{\Delta a}}\int _{0}^{\Delta a}{\sqrt {\frac {\Delta a_{1}-x_{1}}{x_{1}}}}\,dx_{1}.$ Consider rescaling the integral using $\xi =x_{1}/\Delta a$ for $G={\frac {2K_{I}^{2}}{\pi E}}\int _{0}^{1}{\sqrt {\frac {1-\xi }{\xi }}}\,d\xi ,$ where one computes the simpler integral to be $\int _{0}^{1}{\sqrt {\frac {1-\xi }{\xi }}}\,d\xi ={\frac {\pi }{2}},$ leaving the energy release rate as $G={\frac {K_{I}^{2}}{E}},$ the expected relation. In this case, it is not straightforward to obtain $K_{I}$ directly from the loading and geometry of the problem, but since the crack grows straight ahead and the material is linearly elastic, the energy release rate here should be the same as the energy release rate calculated using the other methods. This allows one to indirectly retrieve the stress intensity factor for this problem as $K_{I}={\frac {P}{B}}{\frac {2a}{h}}{\sqrt {\frac {3}{h}}}.$

J - интеграл

В определенных ситуациях скорость выделения энергии $G$ можно рассчитать с помощью J-интеграл , т.е. $G=J$, с использованием

$J=\int _{\Gamma }\left(Wn_{1}-t_{i}\,{\frac {\partial u_{i}}{\partial x_{1}}}\right)\,d\Gamma ,$

где $W$ – плотность энергии упругой деформации, $n_{1}$это $x_{1}$компонента единичного вектора, нормального к $\Gamma$, кривая, используемая для линейного интеграла, $t_{i}$являются компонентами вектора тяги $\mathbf {t} ={\boldsymbol {\sigma }}\cdot \mathbf {n}$, где ${\boldsymbol {\sigma }}$ – тензор напряжений, а $u_{i}$– компоненты вектора смещения.

Этот интеграл равен нулю на простом замкнутом пути и не зависит от пути , что позволяет использовать для расчета любой простой путь, начинающийся и заканчивающийся на берегах трещины. $J$. Чтобы приравнять скорость энерговыделения к J-интегралу, $G=J$, должны быть выполнены следующие условия:

• трещина должна расти прямо вперед, и
• деформация вблизи трещины (заключенной $\Gamma$) должен быть эластичным (не пластиковым).

J-интеграл можно вычислить и с нарушением этих условий, но тогда $G\neq J$. Когда они не нарушаются, можно связать скорость энерговыделения и J-интеграл с модулями упругости и коэффициентами интенсивности напряжений, используя

$G=J={\frac {K_{I}^{2}}{E'}}+{\frac {K_{II}^{2}}{E'}}+{\frac {K_{III}^{2}}{2\mu }}.$

showПример расчета $G$ используя J-интеграл

Double cantilever beam (DCB) specimen under tensile load. J-integral path for the DCB specimen under tensile load. Consider the double cantilever beam specimen shown in the figure, where the crack centered in the beam of height $2h$ has a length of $a$, and a load $P$ is applied to open the crack. Assume that the material is linearly-elastic and that the crack grows straight forward. Consider a rectangular path shown in the second figure: start on the top crack face, (1) go up to the top at $h$, (2) go to the right past the crack tip, (3) go down to the bottom at $-2h$, (4) go along the bottom to the left, and (5) go back up to the bottom crack face. The J-integral is zero along many parts of this path. The material is effectively unloaded behind the crack, so both the strain energy density and traction are zero along (1) and (5), and hence the J-integral. Along (2) and (4) one has $n_{1}=0$ as well as $\mathbf {t} =\mathbf {0}$ (no traction on the free surface), so the J-integral is zero on (2) and (4) as well. This leaves only (3); assuming one is far enough from the crack on (3), the traction term is zero since $u_{1}=0$ and $\sigma _{12}=0$ far from the crack, leaving $J=\int _{\Gamma _{3}}Wn_{1}\,d\Gamma _{3}.$ $n_{1}=1$ along (3), and $W$ is due to bending stress for a cantilever beam $\sigma _{11}(y)=-{\frac {My}{I}}=-{\frac {12Pay}{Bh^{3}}},$ where $B$ is the length into the page. Using $W=\sigma _{11}^{2}/2E$, one now has $J=2\int _{-h/2}^{h/2}{\frac {1}{2E}}\left({\frac {12Pay}{Bh^{3}}}\right)^{2}\,dy,$ where the factor of 2 out front is due to there being 2 cantilever beams. Solving, $G=J={\frac {P^{2}}{B^{2}}}{\frac {12a^{2}}{Eh^{3}}}.$

Вычислительные методы в механике разрушения

Существует несколько методов расчета $G$ с конечными элементами. Хотя прямой расчет J-интеграла возможен (с использованием деформаций и напряжений, выдаваемых методом FEA ), существуют приближенные подходы для некоторых типов роста трещин, которые обеспечивают достаточную точность при простых расчетах. В этом разделе будут подробно рассмотрены некоторые относительно простые методы анализа трещин с использованием численного моделирования.

Узловой метод выпуска

Если трещина растет прямолинейно, скорость энерговыделения можно разложить на сумму трех слагаемых. $G_{i}$ связан с энергией в каждой из трех мод. В результате можно использовать метод узлового высвобождения (NR) для определения $G_{i}$ по результатам ВЭД. Скорость энерговыделения рассчитывается в узлах сетки конечных элементов для трещины начальной длины и продленной на небольшое расстояние. $\Delta a$. Сначала мы вычисляем изменение смещения в интересующем узле. $\Delta {\vec {u}}={\vec {u}}^{(t+1)}-{\vec {u}}^{(t)}$(до и после освобождения узла вершины трещины). Во-вторых, отслеживаем узловую силу ${\vec {F}}$ выдает ФЭА. Наконец, мы можем найти каждый компонент $G$ используя следующие формулы:

Рисунок 1: Раскрытие трещины между двумя последовательными временными шагами с использованием узлового освобождения (NR).

$$G_{1}^{\text{NR}}={\frac {1}{\Delta a}}F_{2}{\frac {\Delta u_{2}}{2}}$$$$G_{2}^{\text{NR}}={\frac {1}{\Delta a}}F_{1}{\frac {\Delta u_{1}}{2}}$$$$G_{3}^{\text{NR}}={\frac {1}{\Delta a}}F_{3}{\frac {\Delta u_{3}}{2}}$$Где $\Delta a$ — ширина элемента, ограничивающего вершину трещины. Точность метода сильно зависит от измельчения сетки, как потому, что от него зависят перемещения и силы, так и потому, что $G=\lim _{\Delta a\to 0}G^{\text{NR}}$. Обратите внимание, что приведенные выше уравнения получены с использованием интеграла закрытия трещины.

Если скорость энерговыделения превысит критическое значение, трещина будет расти. В этом случае выполняется новое моделирование FEA (для следующего временного шага), при котором узел на вершине трещины освобождается. Для ограниченной подложки мы можем просто прекратить применять фиксированные граничные условия Дирихле в узле вершины трещины предыдущего временного шага (т.е. смещения больше не ограничиваются). Для симметричной трещины нам нужно будет обновить геометрию домена, добавив более длинное раскрытие трещины (и, следовательно, создать новую сетку ).

Модифицированный интеграл закрытия трещин

Подобно методу узлового высвобождения, модифицированный интеграл закрытия трещин (MCCI) представляет собой метод расчета скорости выделения энергии с использованием FEA. узловых смещений $(u_{i}^{j})$ и силы $(F_{i}^{j})$. Где $i$ представляет направление, соответствующее декартовым базисным векторам с началом в вершине трещины, и $j$ представляет узловой индекс. MCCI более эффективен в вычислительном отношении, чем метод узлового освобождения, поскольку он требует только одного анализа для каждого приращения роста трещины.

Необходимым условием метода MCCI является единая длина элементов. $(\Delta a)$ вдоль поверхности трещины в $x_{1}-$направление. Кроме того, этот метод требует достаточной дискретизации, чтобы по длине одного элемента поля напряжений были самоподобными . Это означает, что $K(a+\Delta a)\approx K(a)$по мере распространения трещины. Ниже приведены примеры метода MCCI с двумя типами общих конечных элементов.

4-узловые элементы

Рисунок 2: Схема процесса MCCI для 4-узловых линейных прямоугольных элементов.

Квадратные линейные элементы с 4 узлами, показанные на рисунке 2, имеют расстояние между узлами. $j$ и $j+1$ равный $\Delta a.$ Рассмотрим трещину, вершина которой расположена в узле $j.$ Как и в случае с методом узлового освобождения, если бы трещина распространялась на один элемент вдоль линии симметрии (параллельно $x_{1}$-ось) смещение раскрытия трещины будет смещением на вершине предыдущей трещины, т.е. ${\boldsymbol {u^{j}}}$и сила на вершине новой трещины $(j+1)$ было бы ${\boldsymbol {F}}^{j+1}.$ Поскольку рост трещины предполагается автомодельным, смещение в узле $j$ после распространения трещины равна смещению в узле $j-1$ до того, как трещина распространится. Эту же концепцию можно применить к силам в узле $j+1$ и $j.$ Используя тот же метод, который показан в разделе узлового выделения, мы восстанавливаем следующие уравнения для скорости выделения энергии:

$G_{1}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{2}^{j}{\Delta u_{2}^{j-1}}$

$G_{2}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{1}^{j}{\Delta u_{1}^{j-1}}$

$G_{3}^{\text{MCCI}}={\frac {1}{2\Delta a}}F_{3}^{j}{\Delta u_{3}^{j-1}}$

Где $\Delta u_{i}^{j-1}=u_{i}^{(+)j-1}-u_{i}^{(-)j-1}$(смещение выше и ниже поверхности трещины соответственно). Поскольку у нас есть линия симметрии, параллельная трещине, мы можем предположить $u_{i}^{(+)j-1}=-u_{i}^{(-)j-1}.$

Таким образом, $\Delta u_{i}^{j-1}=2u_{i}^{(+)j-1}.$

8-узловые элементы

Рисунок 3: Схема процесса MCCI для 9-узловых квадратных прямоугольных элементов.

Прямоугольные элементы с 8 узлами, показанные на рисунке 3, имеют квадратичные базисные функции . Процесс расчета G такой же, как и для 4-узловых элементов, за исключением того, что $\Delta a$ (рост трещины по одному элементу) теперь является расстоянием от узла $j$ к $j+2.$ Еще раз, принимая во внимание автомодельный прямолинейный рост трещины, скорость энерговыделения можно рассчитать по следующим уравнениям:

$G_{1}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{2}^{j}{\Delta u_{2}^{j-2}}+F_{2}^{j+1}{\Delta u_{2}^{j-1}}\right)$

$G_{2}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{1}^{j}{\Delta u_{1}^{j-2}}+F_{1}^{j+1}{\Delta u_{1}^{j-1}}\right)$

$G_{3}^{\text{MCCI}}={\frac {1}{2\Delta a}}\left(F_{3}^{j}{\Delta u_{3}^{j-2}}+F_{3}^{j+1}{\Delta u_{3}^{j-1}}\right)$

Как и в случае с методом узлового освобождения, точность MCCI сильно зависит от уровня дискретизации вдоль вершины трещины, т.е. $G=\lim _{\Delta a\to 0}G^{\text{MCCI}}.$ Точность также зависит от выбора элемента. Сетка из 8-узловых квадратных элементов может давать более точные результаты, чем сетка из 4-узловых линейных элементов с тем же количеством степеней свободы. в сетке.

Интегральный подход для J

Рисунок 4: Контурный интеграл для J-интеграла

J-интеграл может быть рассчитан непосредственно с использованием сетки конечных элементов и функций формы. Рассмотрим контур области, как показано на рисунке 4, и выберем произвольную гладкую функцию ${\tilde {q}}(x_{1},x_{2})=\sum _{i}N_{i}(x_{1},x_{2}){\tilde {q}}_{i}$ такой, что ${\tilde {q}}=1$ на $\Gamma$ и ${\tilde {q}}=0$ на ${\mathcal {C}}_{1}$.

Для линейно-упругих трещин, растущих прямо вперед, $G=J$. Затем скорость выделения энергии можно рассчитать по площади, ограниченной контуром, используя обновленную формулировку: $J=\int _{\mathcal {A}}(\sigma _{ij}u_{i,1}{\tilde {q}}_{,j}-W{\tilde {q}}_{,1})d{\mathcal {A}}$

Приведенную выше формулу можно применить к любой кольцевой области, окружающей вершину трещины (в частности, можно использовать набор соседних элементов). Этот метод очень точен даже при наличии крупной сетки вокруг вершины трещины (можно выбрать область интегрирования, расположенную далеко, где напряжения и перемещения менее чувствительны к измельчению сетки).

showВывод J-интеграла для метода доменного интеграла

The J-intregral may be expressed over the full contour as follows: $G=J=\int _{\Gamma }(Wn_{1}-t_{i}{\frac {\partial u_{i}}{\partial x_{1}}})d\Gamma =\int _{{\mathcal {C}}_{1}+{\mathcal {C}}_{+}+{\mathcal {C}}_{-}-{\mathcal {C}}}(Wn_{1}-\sigma _{ij}n_{j}{\frac {\partial u_{i}}{\partial x_{1}}}){\tilde {q}}d\Gamma$ With ${\mathcal {C}}={\mathcal {C}}_{1}+{\mathcal {C}}_{+}+{\mathcal {C}}_{-}-\Gamma$. ${\vec {n}}=-{\vec {m}}$, ${\tilde {q}}=0$ on ${\mathcal {C}}_{1}$and the work and stresses cancel out on ${\mathcal {C}}_{+}$and ${\mathcal {C}}_{-}$, hence by application of the divergence theorem this leads to: $J=\int _{\mathcal {C}}(-Wm_{1}+\sigma _{ij}m_{i}{\frac {\partial u_{i}}{\partial x_{1}}})d{\mathcal {C}}=\int _{\mathcal {A}}({\frac {\partial \sigma _{ij}u_{i,1}{\tilde {q}}}{\partial x_{j}}}-{\frac {\partial W{\tilde {q}}}{\partial x_{1}}})d{\mathcal {A}}$ Finally, by noting that ${\frac {\partial W}{\partial x_{1}}}=\sigma _{ij}{\frac {\partial ^{2}u_{i}}{\partial x_{j}\partial x_{1}}}$and using the equilibrium equation: $J=\int _{\mathcal {A}}(\sigma _{ij}u_{i,1}{\tilde {q}}_{,j}-W{\tilde {q}}_{,1})d{\mathcal {A}}$

Особые элементы вершины двумерной трещины

Упомянутые выше методы расчета скорости энерговыделения асимптотически приближаются к реальному решению с повышенной дискретностью, но не могут полностью уловить сингулярность вершины трещины. Более точное моделирование можно выполнить, используя элементы четверти точки вокруг вершины трещины. Эти элементы имеют встроенную особенность, которая более точно создает поля напряжений вокруг вершины трещины. Преимущество метода четверти точки заключается в том, что он позволяет создавать более грубые сетки конечных элементов и значительно снижает вычислительные затраты. Более того, эти элементы получены в результате небольших модификаций обычных конечных элементов без необходимости использования специальных вычислительных программ для анализа. Для целей этого раздела будут рассмотрены упругие материалы, хотя этот метод можно распространить на механику упругопластического разрушения . Предполагая идеальную эластичность, поля напряжений будут испытывать ${\frac {1}{\sqrt {r}}}$ особенность вершины трещины.

8-узловой изопараметрический элемент

Рисунок 5: Сопоставленный и родительский элемент 8-узлового изопараметрического конечного элемента. Обратите внимание на расположение узлов в отображаемом элементе.

Квадратичный элемент с 8 узлами описан на рисунке 5 в обоих родительских пространствах с локальными координатами. $\xi$ и $\eta ,$ и отображаемым элементом в физическом/глобальном пространстве $x$ и $y.$ Родительский элемент отображается из локального пространства в физическое пространство с помощью функций формы. $N_{i}(\xi ,\eta )$ и координаты степени свободы $(x_{i},y_{i}).$ Вершина трещины находится в $\xi =-1,\eta =-1$ или $x=0,y=0.$

$x(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )x_{i}$

$y(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )y_{i}$

Аналогичным образом, перемещения (определяемые как $u\equiv u_{1},v\equiv u_{2}$) также можно отобразить.

$u(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )u_{i}$

$v(\xi ,\eta )=\sum _{i=1}^{8}N_{i}(\xi ,\eta )v_{i}$

Свойством функций формы в методе конечных элементов является компактный носитель , в частности, дельта- свойство Кронекера (т. е. $N_{i}=1$ в узле $i$ и ноль во всех остальных узлах). Это приводит к следующим функциям формы для 8-узловых квадратичных элементов:

$N_{1}={\frac {-(\xi -1)(\eta -1)(1+\eta +\xi )}{4}}$

$N_{2}={\frac {(\xi +1)(\eta -1)(1+\eta -\xi )}{4}}$

$N_{3}={\frac {(\xi +1)(\eta +1)(-1+\eta +\xi )}{4}}$

$N_{4}={\frac {-(\xi -1)(\eta +1)(-1+\eta -\xi )}{4}}$

$N_{5}={\frac {(1-\xi ^{2})(1-\eta )}{2}}$

$N_{6}={\frac {(1+\xi )(1-\eta ^{2})}{2}}$

$N_{7}={\frac {(1-\xi ^{2})(1+\eta )}{2}}$

$N_{8}={\frac {(1-\xi )(1-\eta ^{2})}{2}}$

При рассмотрении линии перед трещиной, коллинеарной $x$- ось (т.е. $N_{i}(\xi ,\eta =-1)$) все базисные функции равны нулю, за исключением $N_{1,2,5}.$

$N_{1}(\xi ,-1)=-{\frac {\xi (1-\xi )}{2}}$

$N_{2}(\xi ,-1)={\frac {\xi (1+\xi )}{2}}$

$N_{5}(\xi ,-1)=(1-\xi ^{2})$

Расчет нормальной деформации включает использование цепного правила для получения производной смещения по отношению к $x.$

$\gamma _{xx}={\frac {\partial u}{\partial x}}=\sum _{i=1,2,5}{\frac {\partial N_{i}}{\partial \xi }}{\frac {\partial \xi }{\partial x}}u_{i}$

Рисунок 6: Треугольный элемент, сопоставленный с прямоугольным элементом с 8 узлами.

Если узлы расположены на прямоугольном элементе равномерно, то деформация не будет содержать особенности. Переместив узлы 5 и 8 в положение на четверть длины $({\tfrac {L}{4}})$ элемента ближе к вершине трещины, как показано на рисунке 5, отображение из $\xi \rightarrow x$ становится:

$x(\xi )={\frac {\xi (1+\xi )}{2}}L+(1-\xi ^{2}){\frac {L}{4}}$

Решение для $\xi$ и взятие производной приводит к:

$\xi (x)=-1+2{\sqrt {\frac {x}{L}}}$

${\frac {\partial \xi }{\partial x}}={\frac {1}{\sqrt {xL}}}$

Подставляя этот результат в уравнение деформации, получаем окончательный результат:

$\gamma _{xx}={\frac {4}{L}}\left({\frac {u_{2}}{2}}-u_{5}\right)+{\frac {1}{\sqrt {xL}}}\left(2u_{5}-{\frac {u_{2}}{5}}\right)$

Перемещение средних узлов в четверть позиции приводит к правильному результату. ${\frac {1}{\sqrt {r}}}$ особенность вершины трещины.

Другие типы элементов

Рисунок 7. Элемент естественного треугольника.

Метод прямоугольных элементов не позволяет легко создавать сетку отдельных элементов вокруг вершины трещины. Это препятствует возможности улавливать угловую зависимость полей напряжений, что имеет решающее значение для определения пути трещины. Кроме того, за исключением краев элемента ${\frac {1}{\sqrt {r}}}$ сингулярность существует в очень маленькой области вблизи вершины трещины. На рисунке 6 показан другой метод четверти точки для моделирования этой особенности. Прямоугольный элемент с 8 узлами можно преобразовать в треугольник. Это делается путем свертывания узлов на линии $\xi =-1$ в положение среднего узла и смещая средние узлы на $\eta =\pm 1$ до четвертьточки. Свернутый прямоугольник может легче окружить вершину трещины, но требует, чтобы края элемента были прямыми, иначе точность расчета коэффициента интенсивности напряжений будет снижена.

Лучшим кандидатом для метода четверти точки является естественный треугольник, как показано на рисунке 7. Геометрия элемента позволяет легко окружить вершину трещины и упростить построение сетки. Следуя той же процедуре, описанной выше, поле перемещений и деформаций для треугольных элементов составляет:

$u=u_{3}+{\sqrt {\frac {x}{L}}}\left[4u_{6}-3u_{3}-u_{1}\right]+{\frac {x}{L}}\left[2u_{1}+2u_{3}-4u_{6}\right]$

$\gamma _{xx}={\frac {\partial u}{\partial x}}={\frac {1}{\sqrt {xL}}}\left[-{\frac {u_{1}}{2}}-{\frac {3u_{3}}{2}}+2u_{6}\right]+{\frac {1}{L}}\left[2u_{1}+2u_{3}-4u_{6}\right]$

Этот метод воспроизводит первые два члена решения Вильямса. с постоянным и единственным членом.

Преимущество метода четверти точки состоит в том, что его можно легко обобщить на трехмерные модели. Это может значительно сократить объем вычислений по сравнению с другими трехмерными методами, но может привести к ошибкам, если кончик трещины распространяется с большой степенью кривизны.

См. также

• Механика разрушения
• Коэффициент интенсивности напряжения
• Вязкость разрушения
• J-интеграл

Внешние ссылки

• по нелинейной механике разрушения. Заметки профессора Джона Хатчинсона (из Гарвардского университета)
• Скорость выделения энергии деформации Гриффита на сайте www.fracturemechanics.org.