Коэффициент интенсивности напряжения

Полярные координаты на вершине трещины.

В механике разрушения коэффициент интенсивности напряжений ( K ) используется для прогнозирования напряженного состояния («интенсивности напряжений») вблизи вершины трещины или надреза , вызванного удаленной нагрузкой или остаточными напряжениями . Это теоретическая конструкция, обычно применяемая к однородному, линейно- упругому материалу, полезная для определения критерия разрушения материалов хрупких и являющаяся критически важным методом в области устойчивости к повреждениям . Эту концепцию также можно применить к материалам, которые демонстрируют небольшую текучесть на вершине трещины.

Величина K зависит от геометрии образца, размера и расположения трещины или надреза, а также величины и распределения нагрузок на материал. Это можно записать как:

$K=\sigma {\sqrt {\pi a}}\,f(a/W)$

где $f(a/W)$ — функция, зависящая от геометрии образца, от длины трещины a и ширины образца W , а σ — приложенное напряжение.

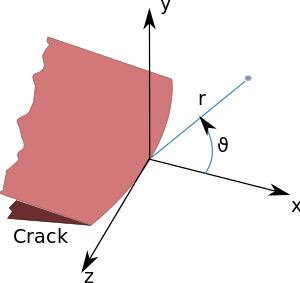
Линейная теория упругости предсказывает, что распределение напряжений ( $\sigma _{ij}$) вблизи вершины трещины в полярных координатах ( $r,\theta$) с началом в вершине трещины, имеет вид

$\sigma _{ij}(r,\theta )={\frac {K}{\sqrt {2\pi r}}}\,f_{ij}(\theta )+\,\,{\rm {higher\,order\,terms}}$

где K – коэффициент интенсивности напряжений (в единицах напряжение × длина ^1/2 ) и $f_{ij}$ представляет собой безразмерную величину, которая меняется в зависимости от нагрузки и геометрии. Теоретически, когда r стремится к 0, напряжение $\sigma _{ij}$ идет в $\infty$ что приводит к сингулярности напряжений. Однако на практике это соотношение нарушается очень близко к кончику (маленькому r ), поскольку пластичность материала обычно возникает при напряжениях, превышающих предел текучести , и линейно-упругое решение больше не применимо. Тем не менее, если пластическая зона вершины трещины мала по сравнению с длиной трещины, асимптотическое распределение напряжений вблизи вершины трещины все еще применимо.

Коэффициенты интенсивности напряжений для различных режимов

Тресковое нагружение в режиме I, режиме II и режиме III.

В 1957 году Дж. Ирвин обнаружил, что напряжения вокруг трещины можно выразить через масштабный коэффициент, называемый коэффициентом интенсивности напряжений . Он обнаружил, что трещина, подвергающаяся любой произвольной нагрузке, может быть разделена на три типа линейно независимых режимов растрескивания. Эти типы нагрузки классифицируются как режим I, II или III, как показано на рисунке. Режим I — это режим раскрытия ( растяжения ), при котором поверхности трещины раздвигаются. в плоскости Режим II — это режим скольжения ( сдвиг ), при котором поверхности трещины скользят друг по другу в направлении, перпендикулярном передней кромке трещины. Режим III — это режим разрыва ( антиплоского сдвига ), при котором поверхности трещины движутся относительно друг друга и параллельно передней кромке трещины. Режим I — наиболее распространенный тип нагрузки, встречающийся в инженерном проектировании.

Для обозначения коэффициента интенсивности напряжения для трех разных режимов используются разные индексы. Коэффициент интенсивности напряжений для I режима обозначается $K_{\rm {I}}$ и применяется к режиму раскрытия трещины. Коэффициент интенсивности напряжений II режима, $K_{\rm {II}}$, относится к режиму скольжения трещины и коэффициенту интенсивности напряжений режима III, $K_{\rm {III}}$, относится к режиму разрыва. Эти факторы формально определяются как:

${\begin{aligned}K_{\rm {I}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yy}(r,0)\\K_{\rm {II}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yx}(r,0)\\K_{\rm {III}}&=\lim _{r\rightarrow 0}{\sqrt {2\pi r}}\,\sigma _{yz}(r,0)\,.\end{aligned}}$

showУравнения для полей напряжений и перемещений

The mode I stress field expressed in terms of $K_{\rm {I}}$ is $\left\{{\begin{aligned}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\1+\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {3\theta }{2}}\end{aligned}}\right\}$, and $\left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{\sqrt {2\pi r}}}\cos {\frac {\theta }{2}}\left\{{\begin{aligned}1+\sin ^{2}{\frac {\theta }{2}}\\\cos ^{2}{\frac {\theta }{2}}\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\end{aligned}}\right\}$. $\sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })$, $\sigma _{xz}=\sigma _{yz}=\sigma _{rz}=\sigma _{\theta z}=0$. The displacements are $\left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[(2\kappa +1)\sin {\frac {\theta }{2}}-\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $\left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {I}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa -1)\cos {\frac {\theta }{2}}-\cos {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa -1)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })$ Where, for plane stress conditions $\kappa ={\frac {(3-\nu )}{(1+\nu )}}$, $\nu _{1}=0$, $\nu _{2}=\nu$, and for plane strain $\kappa =(3-4\nu )$, $\nu _{1}=\nu$, $\nu _{2}=0$. For mode II $\left\{{\begin{aligned}\sigma _{xx}\\\sigma _{yy}\\\sigma _{xy}\end{aligned}}\right\}={\frac {K_{\rm {II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}(2+\cos {\frac {\theta }{2}}\cos {\frac {3\theta }{2}})\\\sin {\frac {\theta }{2}}\cos {\frac {\theta }{2}}\sin {\frac {3\theta }{2}}\\\cos {\frac {\theta }{2}}(1-\sin {\frac {\theta }{2}}\sin {\frac {3\theta }{2}})\end{aligned}}\right\}$ and $\left\{{\begin{aligned}\sigma _{rr}\\\sigma _{\theta \theta }\\\sigma _{r\theta }\end{aligned}}\right\}={\frac {K_{\rm {II}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\\-3\sin {\frac {\theta }{2}}\cos ^{2}{\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}(1-3\sin ^{2}{\frac {\theta }{2}})\end{aligned}}\right\}$, $\sigma _{zz}=\nu _{1}(\sigma _{xx}+\sigma _{yy})=\nu _{1}(\sigma _{rr}+\sigma _{\theta \theta })$, $\sigma _{xz}=\sigma _{yz}=\sigma _{rz}=\sigma _{\theta z}=0$. $\left\{{\begin{aligned}u_{x}\\u_{y}\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[(2\kappa +3)\sin {\frac {\theta }{2}}+\sin {\frac {3\theta }{2}}\right]\\-(1+\nu )\left[(2\kappa -3)\cos {\frac {\theta }{2}}+\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $\left\{{\begin{aligned}u_{r}\\u_{\theta }\end{aligned}}\right\}={\frac {K_{\rm {II}}}{2E}}{\sqrt {\frac {r}{2\pi }}}\left\{{\begin{aligned}(1+\nu )\left[-(2\kappa -1)\sin {\frac {\theta }{2}}+3\sin {\frac {3\theta }{2}}\right]\\(1+\nu )\left[-(2\kappa +1)\cos {\frac {\theta }{2}}+3\cos {\frac {3\theta }{2}}\right]\end{aligned}}\right\}$ $u_{z}=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{xx}+\sigma _{yy})=-\left({\frac {\nu _{2}z}{E}}\right)(\sigma _{rr}+\sigma _{\theta \theta })$ And finally, for mode III $\left\{{\begin{aligned}\sigma _{xz}\\\sigma _{yz}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}-\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}$ $\left\{{\begin{aligned}\sigma _{rz}\\\sigma _{\theta z}\end{aligned}}\right\}={\frac {K_{\rm {III}}}{\sqrt {2\pi r}}}\left\{{\begin{aligned}\sin {\frac {\theta }{2}}\\\cos {\frac {\theta }{2}}\end{aligned}}\right\}$ with $\sigma _{xx}=\sigma _{yy}=\sigma _{rr}=\sigma _{\theta \theta }=\sigma _{zz}=\sigma _{xy}=\sigma _{r\theta }=0$. $u_{z}={\frac {2K_{\rm {III}}}{E}}{\sqrt {\frac {r}{2\pi }}}\left\{2(1+\nu )\sin {\frac {\theta }{2}}\right\}$, $u_{x}=u_{y}=u_{r}=u_{\theta }=0$.

Связь со скоростью энерговыделения и J-интегралом

В плоского напряжения условиях скорость энерговыделения деформации ( $G$) для трещины при нагрузке в чистом режиме I или в чистом режиме II связана с коэффициентом интенсивности напряжений соотношением:

$G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1}{E}}\right)$

$G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1}{E}}\right)$

где $E$ - модуль Юнга и $\nu$ – коэффициент Пуассона материала. Материал предполагается изотропным, однородным и линейно упругим. Предполагалось, что трещина распространяется вдоль направления первоначальной трещины.

Для условий плоской деформации эквивалентное соотношение немного сложнее:

$G_{\rm {I}}=K_{\rm {I}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,$

$G_{\rm {II}}=K_{\rm {II}}^{2}\left({\frac {1-\nu ^{2}}{E}}\right)\,.$

Для загрузки в чистом режиме III

$G_{\rm {III}}=K_{\rm {III}}^{2}\left({\frac {1}{2\mu }}\right)=K_{\rm {III}}^{2}\left({\frac {1+\nu }{E}}\right)$

где $\mu$ – модуль сдвига . Для общей нагрузки при плоской деформации справедлива линейная комбинация:

$G=G_{\rm {I}}+G_{\rm {II}}+G_{\rm {III}}\,.$

Аналогичное соотношение получается для плоского напряжения путем сложения вкладов трех мод.

Приведенные выше соотношения можно использовать и для связи J-интеграла с коэффициентом интенсивности напряжений, поскольку

$G=J=\int _{\Gamma }\left(W~dx_{2}-\mathbf {t} \cdot {\cfrac {\partial \mathbf {u} }{\partial x_{1}}}~ds\right)\,.$

Критический коэффициент интенсивности напряжений

Основная статья: Вязкость разрушения

Коэффициент интенсивности напряжения, $K$, — это параметр, который усиливает величину приложенного напряжения, который включает в себя геометрический параметр $Y$ (тип нагрузки). Интенсивность напряжений в любом режиме ситуации прямо пропорциональна приложенной нагрузке на материал. Если в материале может образоваться очень острая трещина или V- образный надрез , минимальное значение $K_{\mathrm {I} }$ Эмпирически можно определить критическое значение интенсивности напряжений, необходимое для распространения трещины. Это критическое значение, определенное для режима I нагружения при плоской деформации, называется критической вязкостью разрушения ( $K_{\mathrm {Ic} }$) материала. $K_{\mathrm {Ic} }$ имеет единицы напряжения, умноженные на корень расстояния (например, МН/м ^3/2 ). Единицы $K_{\mathrm {Ic} }$ подразумевают, что напряжение разрушения материала должно быть достигнуто на некотором критическом расстоянии, чтобы $K_{\mathrm {Ic} }$ должно быть достигнуто и произойдет распространение трещины. Коэффициент интенсивности критического напряжения режима I, $K_{\mathrm {Ic} }$, является наиболее часто используемым параметром инженерного проектирования в механике разрушения, и, следовательно, его следует понимать, если мы хотим проектировать устойчивые к разрушению материалы, используемые в мостах, зданиях, самолетах или даже колоколах.

Полировка не позволяет обнаружить трещину. Обычно, если трещина видна, она очень близка к критическому напряженному состоянию, прогнозируемому коэффициентом интенсивности напряжения. .

G-критерий

представляет G-критерий собой критерий разрушения , который связывает критический коэффициент интенсивности напряжений (или вязкость разрушения) с коэффициентами интенсивности напряжений для трех режимов. Этот критерий отказа записывается как

$K_{\rm {c}}^{2}=K_{\rm {I}}^{2}+K_{\rm {II}}^{2}+{\frac {E'}{2\mu }}\,K_{\rm {III}}^{2}$

где $K_{\rm {c}}$ это вязкость разрушения, $E'=E/(1-\nu ^{2})$ для плоской деформации и $E'=E$ для плоского напряжения . Критический коэффициент интенсивности напряжений для плоского напряжения часто записывается как $K_{\rm {c}}$.

Примеры

Бесконечная пластина: равномерное одноосное напряжение

Коэффициент интенсивности напряжений для предполагаемой прямой трещины длиной $2a$ перпендикулярно направлению нагрузки, в бесконечной плоскости, с однородным полем напряжений $\sigma$ является $K_{\mathrm {I} }=\sigma {\sqrt {\pi a}}$

Трещина в бесконечной пластине при загрузке режима I.

Трещина в форме пенни в бесконечной области

Коэффициент интенсивности напряжений на вершине копеечной трещины радиусом $a$ в бесконечной области при одноосном растяжении $\sigma$ является $K_{\rm {I}}={\frac {2}{\pi }}\sigma {\sqrt {\pi a}}\,.$

Трещина в форме пенни в бесконечной области при одноосном растяжении.

Конечная пластина: равномерное одноосное напряжение

Если трещина расположена по центру пластины конечной ширины $2b$ и высота $2h$, приближенное соотношение для коэффициента интенсивности напряжений имеет вид $K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\cfrac {1-{\frac {a}{2b}}+0.326\left({\frac {a}{b}}\right)^{2}}{\sqrt {1-{\frac {a}{b}}}}}\right]\,.$ Если трещина расположена не по центру по ширине, т. е. $d\neq b$коэффициент интенсивности напряжений в точке A можно аппроксимировать разложением в ряд $K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\left[1+\sum _{n=2}^{M}C_{n}\left({\frac {a}{b}}\right)^{n}\right]$ где факторы $C_{n}$ можно найти из подгонок к кривым интенсивности напряжения для различных значений $d$. Аналогичное (но не идентичное) выражение можно найти для вершины В трещины. Альтернативные выражения для коэффициентов интенсивности напряжений в точках A и B : $K_{\rm {IA}}=\sigma {\sqrt {\pi a}}\,\Phi _{A}\,\,,K_{\rm {IB}}=\sigma {\sqrt {\pi a}}\,\Phi _{B}$ где ${\begin{aligned}\Phi _{A}&:=\left[\beta +\left({\frac {1-\beta }{4}}\right)\left(1+{\frac {1}{4{\sqrt {\sec \alpha _{A}}}}}\right)^{2}\right]{\sqrt {\sec \alpha _{A}}}\\\Phi _{B}&:=1+\left[{\frac {{\sqrt {\sec \alpha _{AB}}}-1}{1+0.21\sin \left\{8\,\tan ^{-1}\left[\left({\frac {\alpha _{A}-\alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)^{0.9}\right]\right\}}}\right]\end{aligned}}$ с $\beta :=\sin \left({\frac {\pi \alpha _{B}}{\alpha _{A}+\alpha _{B}}}\right)~,~~\alpha _{A}:={\frac {\pi a}{2d}}~,~~\alpha _{B}:={\frac {\pi a}{4b-2d}}~;~~\alpha _{AB}:={\frac {4}{7}}\,\alpha _{A}+{\frac {3}{7}}\,\alpha _{B}\,.$ В приведенных выше выражениях $d$ — расстояние от центра трещины до границы, ближайшей к А. точке Обратите внимание, что когда $d=b$ приведенные выше выражения не упрощаются до приближенного выражения для центрированной трещины.

Трещина в конечной пластине при нагрузке I режима.

Краевая трещина в пластине под одноосным напряжением

Для пластины, имеющей размеры $2h\times b$ содержащая неограниченную краевую трещину длиной $a$, если размерыпластины таковы, что $h/b\geq 0.5$ и $a/b\leq 0.6$, коэффициент интенсивности напряжений при вершина трещины под одноосным напряжением $\sigma$ является $K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[1.122-0.231\left({\frac {a}{b}}\right)+10.55\left({\frac {a}{b}}\right)^{2}-21.71\left({\frac {a}{b}}\right)^{3}+30.382\left({\frac {a}{b}}\right)^{4}\right]\,.$ Для ситуации, когда $h/b\geq 1$ и $a/b\geq 0.3$, коэффициент интенсивности напряжений можно аппроксимироватьк $K_{\rm {I}}=\sigma {\sqrt {\pi a}}\left[{\frac {1+3{\frac {a}{b}}}{2{\sqrt {\pi {\frac {a}{b}}}}\left(1-{\frac {a}{b}}\right)^{3/2}}}\right]\,.$

Краевая трещина в конечной пластине под действием одноосного напряжения.

Бесконечная пластина: наклонная трещина в поле двухосных напряжений

Для наклонной трещины длиной $2a$ в поле двухосных напряжений с напряжением $\sigma$ в $y$-направление и $\alpha \sigma$ в $x$-направлении, коэффициенты интенсивности напряжений ${\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {\pi a}}\left(\cos ^{2}\beta +\alpha \sin ^{2}\beta \right)\\K_{\rm {II}}&=\sigma {\sqrt {\pi a}}\left(1-\alpha \right)\sin \beta \cos \beta \end{aligned}}$ где $\beta$ угол, образуемый трещиной с $x$-ось.

Наклонная трещина в тонкой пластине под действием двухосной нагрузки.

Трещина в пластине под действием точечной плоскостной силы

Рассмотрим пластину с размерами $2h\times 2b$ содержащая трещину длиной $2a$. Точечная сила с компонентами $F_{x}$ и $F_{y}$ применяется в точке ( $x,y$) тарелки. Для ситуации, когда пластина велика по сравнению с размером трещины и расположение силы относительно близко к трещине, т.е. $h\gg a$, $b\gg a$, $x\ll b$, $y\ll h$, пластину можно считать бесконечной. В этом случае для коэффициентов интенсивности напряжений $F_{x}$ у вершины трещины B ( $x=a$) являются ${\begin{aligned}K_{\rm {I}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}+{\frac {1}{\kappa -1}}H_{1}\right]\\K_{\rm {II}}&={\frac {F_{x}}{2{\sqrt {\pi a}}}}\left[G_{2}+{\frac {1}{\kappa +1}}H_{2}\right]\end{aligned}}$ где ${\begin{aligned}G_{1}&=1-{\text{Re}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\,,\,\,G_{2}=-{\text{Im}}\left[{\frac {a+z}{\sqrt {z^{2}-a^{2}}}}\right]\\H_{1}&={\text{Re}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\,,\,\,H_{2}=-{\text{Im}}\left[{\frac {a({\bar {z}}-z)}{({\bar {z}}-a){\sqrt {{\bar {z}}^{2}-a^{2}}}}}\right]\end{aligned}}$ с $z=x+iy$, ${\bar {z}}=x-iy$, $\kappa =3-4\nu$ для плоской деформации , $\kappa =(3-\nu )/(1+\nu )$ для плоского напряжения и $\nu$ это коэффициент Пуассона .Факторы интенсивности стресса для $F_{y}$ на кончике B находятся ${\begin{aligned}K_{\rm {I}}&={\frac {F_{y}}{2{\sqrt {\pi a}}}}\left[G_{2}-{\frac {1}{\kappa +1}}H_{2}\right]\\K_{\rm {II}}&=-{\frac {F_{y}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\left[G_{1}-{\frac {1}{\kappa -1}}H_{1}\right]\,.\end{aligned}}$ Коэффициенты интенсивности напряжений на вершине А ( $x=-a$) можно определить из приведенных выше соотношений. Для нагрузки $F_{x}$ на месте $(x,y)$, $K_{\rm {I}}(-a;x,y)=-K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=K_{\rm {II}}(a;-x,y)\,.$ Аналогично для нагрузки $F_{y}$, $K_{\rm {I}}(-a;x,y)=K_{\rm {I}}(a;-x,y)\,,\,\,K_{\rm {II}}(-a;x,y)=-K_{\rm {II}}(a;-x,y)\,.$

Трещина в пластине под действием локализованной силы с составляющими $F_{x}$ и $F_{y}$.

Загруженная трещина в тарелке

Если трещина нагружена точечной силой $F_{y}$ расположен по адресу $y=0$ и $-a<x<a$, коэффициенты интенсивности напряжений в точке B равны $K_{\rm {I}}={\frac {F_{y}}{2{\sqrt {\pi a}}}}{\sqrt {\frac {a+x}{a-x}}}\,,\,\,K_{\rm {II}}=-{\frac {F_{x}}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\,.$ Если сила распределена равномерно между $-a<x<a$, то коэффициент интенсивности напряжений на вершине B равен $K_{\rm {I}}={\frac {1}{2{\sqrt {\pi a}}}}\int _{-a}^{a}F_{y}(x)\,{\sqrt {\frac {a+x}{a-x}}}\,{\rm {d}}x\,,\,\,K_{\rm {II}}=-{\frac {1}{2{\sqrt {\pi a}}}}\left({\frac {\kappa -1}{\kappa +1}}\right)\int _{-a}^{a}F_{y}(x)\,{\rm {d}}x,\,.$

Загруженная трещина в тарелке.

Стопка параллельных трещин в бесконечной пластине

Если расстояние между трещинами много больше длины трещины (h >> a), то эффектом взаимодействия соседних трещин можно пренебречь и коэффициент интенсивности напряжений будет равен коэффициенту интенсивности одиночной трещины длиной 2a.

Тогда коэффициент интенсивности напряжений в вершине трещины равен

${\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {\pi a}}\end{aligned}}$

Если длина трещины намного больше расстояния (a >> h), трещины можно рассматривать как стопку полубесконечных трещин.

Тогда коэффициент интенсивности напряжений в вершине трещины равен

${\begin{aligned}K_{\rm {I}}&=\sigma {\sqrt {h}}\end{aligned}}$

Компактный образец на растяжение

Коэффициент интенсивности напряжений в вершине трещины компактного растянутого образца равен ${\begin{aligned}K_{\rm {I}}&={\frac {P}{B}}{\sqrt {\frac {\pi }{W}}}\left[16.7\left({\frac {a}{W}}\right)^{1/2}-104.7\left({\frac {a}{W}}\right)^{3/2}+369.9\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-573.8\left({\frac {a}{W}}\right)^{7/2}+360.5\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}$ где $P$ приложенная нагрузка, $B$ - толщина образца, $a$ длина трещины, а $W$ – ширина образца.

Компактный образец на растяжение для испытаний на вязкость разрушения.

Образец для одностороннего изгиба с надрезом

Коэффициент интенсивности напряжений в вершине трещины однокромочного образца с надрезом равен ${\begin{aligned}K_{\rm {I}}&={\frac {4P}{B}}{\sqrt {\frac {\pi }{W}}}\left[1.6\left({\frac {a}{W}}\right)^{1/2}-2.6\left({\frac {a}{W}}\right)^{3/2}+12.3\left({\frac {a}{W}}\right)^{5/2}\right.\\&\qquad \left.-21.2\left({\frac {a}{W}}\right)^{7/2}+21.8\left({\frac {a}{W}}\right)^{9/2}\right]\end{aligned}}$ где $P$ приложенная нагрузка, $B$ - толщина образца, $a$ длина трещины, а $W$ – ширина образца.

Образец для изгиба с одной кромкой (также называемый образцом для трехточечного изгиба) для испытаний на вязкость разрушения.

См. также

• Механика разрушения
• Вязкость разрушения
• Скорость выделения энергии деформации
• J-интеграл
• Теория разрушения материала
• Закон Парижа

Внешние ссылки

• Катиресан, К.; Сюй, ТМ ; Брюссат, Т.Р., 1984, Передовые методы анализа жизни. Том 2. Методы анализа роста трещин для крепежных проушин
• Фактор интенсивности напряжения на сайте www.fracturemechanics.org , Боб МакГинти.