Жесткое уравнение

В математике — жесткое уравнение это дифференциальное уравнение , для которого определенные численные методы решения уравнения численно нестабильны , если только размер шага не считается чрезвычайно малым. Сформулировать точное определение жесткости оказалось сложно, но основная идея заключается в том, что уравнение включает в себя некоторые члены, которые могут привести к быстрому изменению решения.

При численном интегрировании дифференциального уравнения можно было бы ожидать, что необходимый размер шага будет относительно небольшим в области, где кривая решения сильно варьируется, и относительно большим, когда кривая решения выпрямляется и приближается к линии с наклоном, близким к нулю. Для некоторых проблем это не так. Чтобы численный метод дал надежное решение дифференциальной системы, иногда требуется, чтобы размер шага был на неприемлемо малом уровне в области, где кривая решения очень гладкая. Это явление известно как жесткость . В некоторых случаях могут существовать две разные задачи с одним и тем же решением, но одна не является жесткой, а другая — жесткой. Следовательно, это явление не может быть свойством точного решения, поскольку оно одинаково для обеих задач и должно быть свойством самой дифференциальной системы. Такие системы поэтому известны как жесткие системы .

Мотивирующий пример

Явные численные методы, демонстрирующие неустойчивость при интегрировании жесткого обыкновенного дифференциального уравнения

Рассмотрим задачу начального значения

$\,y'(t)=-15y(t),\quad t\geq 0,\quad y(0)=1.$ ( 1 )

Точное решение (показано голубым цветом):

$y(t)=e^{-15t},\quad y(t)\to 0{\text{ as }}t\to \infty .$ ( 2 )

Мы ищем численное решение , которое демонстрирует такое же поведение.

Рисунок (справа) иллюстрирует численные проблемы для различных числовых интеграторов, применяемых в уравнении.

1. Метод Эйлера с шагом $h={\tfrac {1}{4}}$ сильно колеблется и быстро выходит за пределы диапазона графика (показано красным).
2. Метод Эйлера с половиной шага, $h={\tfrac {1}{8}}$, дает решение в пределах границ графика, но колеблется около нуля (показано зеленым).
3. Трапециевидный метод (т. е. двухэтапный метод Адамса – Моултона ) имеет вид
   $y_{n+1}=y_{n}+{\tfrac {1}{2}}h{\bigl (}f(t_{n},y_{n})+f(t_{n+1},y_{n+1}){\bigr )},$ ( 3 )
   где $y'=f(t,y)$. Применение этого метода вместо метода Эйлера дает гораздо лучший результат (синий). Численные результаты монотонно убывают до нуля, как и точное решение.

Одним из наиболее ярких примеров жестких обыкновенных дифференциальных уравнений (ОДУ) является система, описывающая химическую реакцию Робертсона:

${\begin{aligned}\mathrm {A} \xrightarrow {0.04} &\mathrm {B} \\\mathrm {B} +\mathrm {B} \xrightarrow {3\cdot 10^{7}} &\mathrm {C} +\mathrm {B} \\\mathrm {B} +\mathrm {C} \xrightarrow {1\cdot 10^{4}} &\mathrm {A} +\mathrm {C} \end{aligned}}$

${\begin{aligned}{\dot {x}}&=-0.04x+10^{4}y\cdot z\\{\dot {y}}&=0.04x-10^{4}y\cdot z-3\cdot 10^{7}y^{2}\\{\dot {z}}&=3\cdot 10^{7}y^{2}\end{aligned}}$

( 4 )

Если рассматривать эту систему на коротком интервале, например, $t\in [0,40]$ проблем с численным интегрированием нет. Однако если интервал очень велик (10 ¹¹ скажем), то многие стандартные коды не могут правильно его интегрировать.

Коэффициент жесткости

Рассмотрим линейную неоднородную систему с постоянными коэффициентами

$\mathbf {y} '=\mathbf {A} \mathbf {y} +\mathbf {f} (x),$ ( 5 )

где $\mathbf {y} ,\mathbf {f} \in \mathbb {R} ^{n}$ и $\mathbf {A}$ является постоянной, диагонализируемой, $n\times n$ матрица с собственными значениями $\lambda _{t}\in \mathbb {C} ,t=1,2,\ldots ,n$ (предполагается различными) и соответствующие собственные векторы $\mathbf {c} _{t}\in \mathbb {C} ^{n},t=1,2,\ldots ,n$. Общее решение ( 5 ) принимает вид

$\mathbf {y} (x)=\sum _{t=1}^{n}\kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}+\mathbf {g} (x),$ ( 6 )

где $\kappa _{t}$ являются произвольными константами и $\mathbf {g} (x)$ является частным интегралом. Теперь предположим, что

$\operatorname {Re} (\lambda _{t})<0,\qquad t=1,2,\ldots ,n,$ ( 7 )

из чего следует, что каждое из слагаемых $e^{\lambda _{t}x}\mathbf {c} _{t}\to 0$ как $x\to \infty$, так что решение $\mathbf {y} (x)$ подходы $\mathbf {g} (x)$ асимптотически как $x\to \infty$; термин $e^{\lambda _{t}x}\mathbf {c} _{t}$ будет монотонно затухать, если $\lambda _{t}$ действительно и синусоидально, если $\lambda _{t}$ является сложным.

Устный перевод $x$ быть временем (как это часто бывает в физических проблемах), ${\textstyle \sum _{t=1}^{n}\kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}}$ называется переходным решением и $\mathbf {g} (x)$ стационарное решение . Если $\left|\operatorname {Re} (\lambda _{t})\right|$ велико, то соответствующий член $\kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}$ быстро распадется, так как $x$ увеличивается и поэтому называется быстрым переходным процессом ; если $\left|\operatorname {Re} (\lambda _{t})\right|$ мал, соответствующий член $\kappa _{t}e^{\lambda _{t}x}\mathbf {c} _{t}$ затухает медленно и называется медленным переходным процессом . Позволять ${\overline {\lambda }},{\underline {\lambda }}\in \{\lambda _{t},t=1,2,\ldots ,n\}$ определяться

${\bigl |}\operatorname {Re} ({\overline {\lambda }}){\bigr |}\geq {\bigl |}\operatorname {Re} (\lambda _{t}){\bigr |}\geq {\bigl |}\operatorname {Re} ({\underline {\lambda }}){\bigr |},\qquad t=1,2,\ldots ,n$ ( 8 )

так что $\kappa _{t}e^{{\overline {\lambda }}x}\mathbf {c} _{t}$ является самым быстрым переходным процессом и $\kappa _{t}e^{{\underline {\lambda }}x}\mathbf {c} _{t}$ самый медленный. Теперь мы определяем коэффициент жесткости как

${\frac {{\bigl |}\operatorname {Re} ({\overline {\lambda }}){\bigr |}}{{\bigl |}\operatorname {Re} ({\underline {\lambda }}){\bigr |}}}.$ ( 9 )

Характеристика жесткости

В этом разделе мы рассмотрим различные аспекты явления жесткости. «Феномен», вероятно, более подходящее слово, чем «свойство», поскольку последнее скорее подразумевает, что жесткость можно определить в точных математических терминах; оказывается, что сделать это удовлетворительным образом невозможно даже для ограниченного класса линейных систем с постоянными коэффициентами. Мы также увидим несколько качественных утверждений, которые могут быть сделаны (и в большинстве случаев были сделаны) в попытке сформулировать понятие жесткости, и сформулируем, вероятно, наиболее удовлетворительное из них как «определение» жесткости.

Дж. Д. Ламберт определяет жесткость следующим образом:

Если численный метод с конечной областью абсолютной устойчивости , примененный к системе с любыми начальными условиями , вынужден использовать на некотором интервале интегрирования длину шага, чрезмерно малую по отношению к гладкости точного решения на этом интервале система называется жесткой . , то на этом интервале

Существуют и другие характеристики, которые демонстрируются во многих примерах жестких задач, но для каждой из них есть контрпримеры, поэтому эти характеристики не могут служить хорошим определением жесткости. Тем не менее, определения, основанные на этих характеристиках, широко используются некоторыми авторами и являются хорошим ключом к определению наличия жесткости. Ламберт называет их «утверждениями», а не определениями по вышеупомянутым причинам. Некоторые из них:

1. Линейная система постоянных коэффициентов является жесткой, если все ее собственные значения имеют отрицательную действительную часть и коэффициент жесткости велик.
2. Жесткость возникает, когда требования к стабильности, а не к точности, ограничивают длину шага.
3. Жесткость возникает, когда некоторые компоненты раствора распадаются гораздо быстрее, чем другие.

Этимология

Происхождение термина «жесткость» точно не установлено. По словам Джозефа Окленда Хиршфельдера , термин «жесткий» используется потому, что такие системы соответствуют тесной связи между приводом приводными сервомеханизмами и . По словам Ричарда. Л. Берден и Дж. Дуглас Фейрс,

Значительные трудности могут возникнуть при применении стандартных численных методов для аппроксимации решения дифференциального уравнения , когда точное решение содержит члены вида $e^{\lambda t}$, где $\lambda$ комплексное число с отрицательной действительной частью.

. . .

Проблемы, связанные с быстро затухающими переходными решениями, естественным образом возникают в самых разных приложениях, включая исследование пружин и систем демпфирования, анализ систем управления и проблемы химической кинетики . Все это примеры класса задач, называемых жесткими (математической жесткостью) системами дифференциальных уравнений из-за их применения при анализе движения пружинных и массовых систем, имеющих большие константы пружины (физическая жесткость ).

Например, задача начального значения

$m{\ddot {x}}+c{\dot {x}}+kx=0,\qquad x(0)=x_{0},\qquad {\dot {x}}(0)=0,$ ( 10 )

с $m=1$, $c=1001$, $k=1000$, можно записать в виде ( 5 ) с $n=2$ и

$\mathbf {A} ={\begin{pmatrix}0&1\\-1000&-1001\end{pmatrix}},\qquad \mathbf {f} (t)={\begin{pmatrix}0\\0\end{pmatrix}},\qquad \mathbf {x} (0)={\begin{pmatrix}x_{0}\\0\end{pmatrix}},$ ( 11 )

и имеет собственные значения ${\overline {\lambda }}=-1000,{\underline {\lambda }}=-1$. Оба собственных значения имеют отрицательную действительную часть, а коэффициент жесткости равен

${\frac {|-1000|}{|-1|}}=1000,$ ( 12 )

что довольно велико. Тогда система ( 10 ) заведомо удовлетворяет утверждениям 1 и 3. Здесь жесткость пружины $k$ велика, а константа затухания $c$ еще больше. (хотя «большой» не является четко определенным термином, но чем больше вышеуказанные величины, тем более выраженным будет эффект жесткости.)Точное решение ( 10 ) есть

$x(t)=x_{0}\left(-{\frac {1}{999}}e^{-1000t}+{\frac {1000}{999}}e^{-t}\right)\approx x_{0}e^{-t}.$ ( 13 )

Уравнение 13 ведет себя очень похоже на простую экспоненту. $x_{0}e^{-t}$, но наличие $e^{-1000t}$ члена, даже с небольшим коэффициентом, достаточно, чтобы сделать численные вычисления очень чувствительными к размеру шага. Стабильное интегрирование ( 10 ) требует очень маленького шага до достижения гладкой части кривой решения, что приводит к ошибке, намного меньшей, чем требуется для точности. Таким образом, система также удовлетворяет утверждению 2 и определению Ламберта.

А-стабильность

Поведение численных методов решения жестких задач можно проанализировать, применив эти методы к тестовому уравнению $y'=ky$ при условии начального состояния $y(0)=1$ с $k\in \mathbb {C}$. Решение этого уравнения есть $y(t)=e^{kt}$. Это решение приближается к нулю, поскольку $t\to \infty$ когда $\operatorname {Re} (k)<0.$ Если численный метод также демонстрирует такое поведение (при фиксированном размере шага), то метод называется A-стабильным. Численный метод, который является L-стабильным (см. ниже), обладает более сильным свойством: решение приближается к нулю за один шаг, когда размер шага стремится к бесконечности. А-стабильные методы не вызывают проблем нестабильности, описанных в мотивирующем примере.

Методы Рунге-Кутты

Методы Рунге – Кутты, примененные к проверочному уравнению $y'=k\cdot y$ принять форму $y_{n+1}=\phi (hk)\cdot y_{n}$, и по индукции $y_{n}={\bigl (}\phi (hk){\bigr )}^{n}\cdot y_{0}$. Функция $\phi$ называется функцией устойчивости . Таким образом, условие, $y_{n}\to 0$ как $n\to \infty$ эквивалентно $|\phi (hk)|<1$. Это мотивирует определение области абсолютной устойчивости (иногда называемой просто областью устойчивости ), которая представляет собой множество ${\bigl \{}z\in \mathbb {C} \,{\big |}\,|\phi (z)|<1{\bigr \}}$. Метод A-стабилен, если область абсолютной устойчивости содержит множество ${\bigl \{}z\in \mathbb {C} \,{\big |}\,\operatorname {Re} (z)<0{\bigr \}}$, то есть левая полуплоскость.

Пример: методы Эйлера

Розовым диском показана область устойчивости метода Эйлера.

Рассмотрим методы Эйлера, описанные выше. Явный метод Эйлера, примененный к тестовому уравнению $y'=k\cdot y$ является

$y_{n+1}=y_{n}+h\cdot f(t_{n},y_{n})=y_{n}+h\cdot (ky_{n})=y_{n}+h\cdot k\cdot y_{n}=(1+h\cdot k)y_{n}.$

Следовательно, $y_{n}=(1+hk)^{n}\cdot y_{0}$ с $\phi (z)=1+z$. Таким образом, область абсолютной устойчивости для этого метода равна ${\bigl \{}z\in \mathbb {C} \,{\big |}\,|1+z|<1{\bigr \}}$ это диск, изображенный справа. Метод Эйлера не является A-стабильным.

Мотивирующим примером был $k=-15$. Значение z при выборе размера шага $h={\tfrac {1}{4}}$ является $z=-15\times {\tfrac {1}{4}}=-3.75$, что находится за пределами области устойчивости. Действительно, численные результаты не сходятся к нулю. Однако с размером шага $h={\tfrac {1}{8}}$, у нас есть $z=-1.875$ что находится как раз внутри области устойчивости, и численные результаты сходятся к нулю, хотя и довольно медленно.

Пример: Трапециевидный метод

Розовая область — это область устойчивости трапециевидного метода.

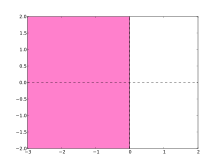
Рассмотрим трапециевидный метод

$y_{n+1}=y_{n}+{\tfrac {1}{2}}h\cdot {\bigl (}f(t_{n},y_{n})+f(t_{n+1},y_{n+1}){\bigr )},$

применительно к проверочному уравнению $y'=k\cdot y$, является

$y_{n+1}=y_{n}+{\tfrac {1}{2}}h\cdot \left(ky_{n}+ky_{n+1}\right).$

Решение для $y_{n+1}$ урожайность

$y_{n+1}={\frac {1+{\frac {1}{2}}hk}{1-{\frac {1}{2}}hk}}\cdot y_{n}.$

Таким образом, функция устойчивости равна

$\phi (z)={\frac {1+{\frac {1}{2}}z}{1-{\frac {1}{2}}z}}$

и область абсолютной устойчивости

$\left\{z\in \mathbb {C} \ \left|\ \left|{\frac {1+{\frac {1}{2}}z}{1-{\frac {1}{2}}z}}\right|<1\right.\right\}.$

Эта область содержит левую полуплоскость, поэтому трапециевидный метод A-стабилен. Фактически область устойчивости идентична левой полуплоскости, и, следовательно, численное решение $y'=k\cdot y$ сходится к нулю тогда и только тогда, когда сходится точное решение. Тем не менее, трапециевидный метод не обладает идеальным поведением: он затухает все затухающие компоненты, но быстро затухающие компоненты затухают лишь очень слабо, поскольку $\phi (z)\to 1$ как $z\to -\infty$. Это привело к концепции L-стабильности : метод является L-стабильным, если он A-стабилен и $|\phi (z)|\to 0$ как $z\to \infty$. Трапециевидный метод является A-стабильным, но не L-стабильным. Неявный метод Эйлера является примером L-стабильного метода.

Общая теория

Функция устойчивости метода Рунге–Кутты с коэффициентами $\mathbf {A}$ и $\mathbf {b}$ дается

$\phi (z)={\frac {\det \left(\mathbf {I} -z\mathbf {A} +z\mathbf {e} \mathbf {b} ^{\mathsf {T}}\right)}{\det(\mathbf {I} -z\mathbf {A} )}},$

где $\mathbf {e}$ обозначает вектор со всеми единицами. Это рациональная функция (один многочлен делится на другой).

Явные методы Рунге – Кутты имеют строго нижнюю треугольную матрицу коэффициентов. $\mathbf {A}$ и, следовательно, их функция устойчивости является полиномом. Отсюда следует, что явные методы Рунге–Кутты не могут быть A-устойчивыми.

Функция устойчивости неявных методов Рунге – Кутты часто анализируется с использованием звезд порядка . Звезда порядка для метода с функцией устойчивости $\phi$ определяется как набор ${\bigl \{}z\in \mathbb {C} \,{\big |}\,|\phi (z)|>|e^{z}|{\bigr \}}$. Метод A-стабилен тогда и только тогда, когда его функция устойчивости не имеет полюсов в левой плоскости и его порядковая звезда не содержит чисто мнимых чисел.

Многошаговые методы

Линейные многошаговые методы имеют вид

$y_{n+1}=\sum _{i=0}^{s}a_{i}y_{n-i}+h\sum _{j=-1}^{s}b_{j}f\left(t_{n-j},y_{n-j}\right).$

Применительно к проверочному уравнению они становятся

$y_{n+1}=\sum _{i=0}^{s}a_{i}y_{n-i}+hk\sum _{j=-1}^{s}b_{j}y_{n-j},$

который можно упростить до

$\left(1-b_{-1}z\right)y_{n+1}-\sum _{j=0}^{s}\left(a_{j}+b_{j}z\right)y_{n-j}=0$

где $z=hk$. Это линейное рекуррентное соотношение . Метод A-стабилен, если все решения $\{y_{n}\}$ рекуррентного соотношения сходятся к нулю, когда $\operatorname {Re} (z)<0$. Характеристический полином

$\Phi (z,w)=w^{s+1}-\sum _{i=0}^{s}a_{i}w^{s-i}-z\sum _{j=-1}^{s}b_{j}w^{s-j}.$

Все решения сходятся к нулю при заданном значении $z$ если все решения $w$ из $\Phi (z,w)=0$ лежат в единичном круге.

Тогда областью абсолютной устойчивости многошагового метода указанного вида является совокупность всех $z\in \mathbb {C}$ ради чего все $w$ такой, что $\Phi (z,w)=0$ удовлетворить $|w|<1$. Опять же, если это множество содержит левую полуплоскость, многошаговый метод называется A-стабильным.

Пример: метод Адамса – Башфорта второго порядка.

Розовая область представляет собой область устойчивости метода Адамса – Башфорта второго порядка.

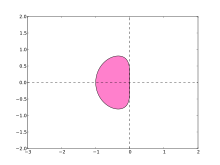
Определим область абсолютной устойчивости двухшагового метода Адамса–Бэшфорта.

$y_{n+1}=y_{n}+h\left({\tfrac {3}{2}}f(t_{n},y_{n})-{\tfrac {1}{2}}f(t_{n-1},y_{n-1})\right).$

Характеристический полином

$\Phi (w,z)=w^{2}-\left(1+{\tfrac {3}{2}}z\right)w+{\tfrac {1}{2}}z=0$

у которого есть корни

$w={\tfrac {1}{2}}\left(1+{\tfrac {3}{2}}z\pm {\sqrt {1+z+{\tfrac {9}{4}}z^{2}}}\right),$

таким образом, область абсолютной устойчивости

$\left\{z\in \mathbb {C} \ \left|\ \left|{\tfrac {1}{2}}\left(1+{\tfrac {3}{2}}z\pm {\sqrt {1+z+{\tfrac {9}{4}}z^{2}}}\right)\right|<1\right.\right\}.$

Этот регион показан справа. Он не включает всю левую полуплоскость (фактически он включает только действительную ось между $-1\leq z\leq 0$), поэтому метод Адамса – Башфорта не является A-стабильным.

Общая теория

Явные многошаговые методы никогда не могут быть A-стабильными, как и явные методы Рунге–Кутты. Неявные многошаговые методы могут быть A-стабильными только в том случае, если их порядок не превышает 2. Последний результат известен как второй Далквиста барьер ; это ограничивает полезность линейных многошаговых методов для жестких уравнений. Примером A-стабильного метода второго порядка является упомянутое выше правило трапеций, которое также можно рассматривать как линейный многошаговый метод.

См. также

• Формула обратного дифференцирования — семейство неявных методов, специально используемых для решения жестких дифференциальных уравнений.
• Номер условия
• Дифференциальное включение , расширение понятия дифференциального уравнения, которое допускает разрывы, отчасти как способ обойти некоторые проблемы жесткости.
• Явные и неявные методы

Ссылки

• Берден, Ричард Л.; Фейрес, Дж. Дуглас (1993), Численный анализ (5-е изд.), Бостон: Приндл, Вебер и Шмидт , ISBN  0-534-93219-3 .
• Далквист, Гермунд (1963), «Специальная проблема устойчивости линейных многошаговых методов», BIT , 3 (1): 27–43, doi : 10.1007/BF01963532 , hdl : 10338.dmlcz/103497 , S2CID   120241743 .
• Эберли, Дэвид (2008), Анализ устойчивости систем дифференциальных уравнений (PDF) .
• Эле, Б.Л. (1969), Об аппроксимациях Паде экспоненциальной функции и A-стабильных методах численного решения начальных задач (PDF) , Университет Ватерлоо .
• Гир, К.В. (1971), Численные задачи начального значения в обыкновенных дифференциальных уравнениях , Энглвуд Клиффс: Прентис Холл , Бибкод : 1971nivp.book.....G .
• Гир, К.В. (1981), «Численное решение обыкновенных дифференциальных уравнений: осталось ли что-нибудь сделать?», SIAM Review , 23 (1): 10–24, doi : 10.1137/1023002 .
• Хайрер, Эрнст; Ваннер, Герхард (1996), Решение обыкновенных дифференциальных уравнений II: жесткие и дифференциально-алгебраические задачи (второе изд.), Берлин: Springer-Verlag , ISBN  978-3-540-60452-5 .
• Хиршфельдер, Дж.О. (1963), «Прикладная математика, используемая в теоретической химии», Симпозиум Американского математического общества : 367–376 .
• Изерлес, Арье; Норсетт, Сиверт (1991), Звезды Ордена , Чепмен и Холл , ISBN  978-0-412-35260-7 .
• Крейциг, Эрвин (1972), Высшая инженерная математика (3-е изд.), Нью-Йорк: Wiley , ISBN  0-471-50728-8 .
• Ламберт, Дж. Д. (1977), Д. Джейкобс (редактор), «Проблема начального значения для обыкновенных дифференциальных уравнений», Состояние дел в численном анализе , Нью-Йорк: Academic Press : 451–501 .
• Ламберт, JD (1992), Численные методы для обыкновенных дифференциальных систем , Нью-Йорк: Wiley , ISBN  978-0-471-92990-1 .
• Мэтьюз, Джон; Финк, Куртис (1992), Численные методы с использованием MATLAB .
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007). «Раздел 17.5. Жесткие системы уравнений» . Численные рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-88068-8 . Архивировано из оригинала 11 августа 2011 г. Проверено 17 августа 2011 г.
• Шампин, LF; Гир, К.В. (1979), «Взгляд пользователя на решение жестких обыкновенных дифференциальных уравнений» , SIAM Review , 21 (1): 1–17, doi : 10.1137/1021001 .
• Ваннер, Герхард; Хайрер, Эрнст; Норсетт, Сиверт (1978), «Звезды порядка и теория стабильности», BIT , 18 (4): 475–489, doi : 10.1007/BF01932026 , S2CID   8824105 .
• Устойчивость методов Рунге-Кутты [1]

Внешние ссылки

• Введение в физическое моделирование: энергетические функции и жесткость
• Жесткие системы Лоуренс Ф. Шампин и Скип Томпсон Scholarpedia , 2(3):2855. doi:10.4249/scholarpedia.2855