Орбита Марса
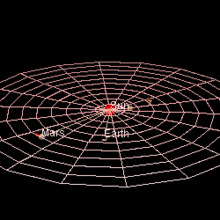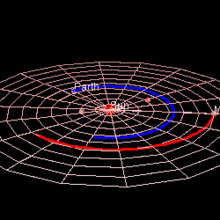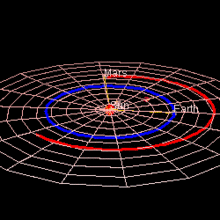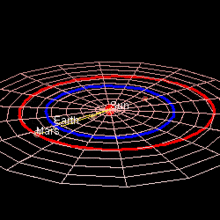


Марс имеет орбиту с большой полуосью 1,524 астрономических единиц (228 миллионов км) (12,673 световых минут) и эксцентриситетом 0,0934. [1] [2] Планета обращается вокруг Солнца за 687 дней. [3] и при этом преодолевает 9,55 а.е., [4] средняя орбитальная скорость составляет 24 км/с.
Эксцентриситет больше, чем у любой другой планеты, кроме Меркурия, и это вызывает большую разницу между расстояниями афелия и перигелия - они составляют соответственно 1,639 и 1,405 а.е. [5]
Изменения на орбите
[ редактировать ]Марс находится в процессе долгосрочного увеличения эксцентриситета. Оно достигло минимума 0,079 около 19 тысячелетий назад и достигнет максимума примерно на уровне 0,105 примерно через 24 тысячелетия (и с расстоянием в перигелии всего 1,3621 астрономической единицы ). Орбита временами близка к круговой: она была 0,002 1,35 миллиона лет назад и достигнет аналогичного минимума через 1,05 миллиона лет в будущем. [ нужны разъяснения ] Максимальный эксцентриситет между этими двумя крайними минимумами составляет 0,12 примерно за 200 тысяч лет. [6]
Оппозиции
[ редактировать ]Марс достигает оппозиции , когда разница между его геоцентрической долготой и долготой Солнца составляет 180°. В момент, близкий к противостоянию (в течение 8,5 дней), расстояние Земля-Марс настолько мало, насколько оно возможно в течение этого 780-дневного синодического периода . [7] Каждое противостояние имеет определенное значение, поскольку Марс виден с Земли всю ночь, высоко и полностью освещен, но особый интерес возникает, когда Марс находится вблизи перигелия, потому что в это время Марс также находится ближе всего к Земле. За одной перигелической оппозицией следует другая либо 15, либо 17 лет спустя. Фактически за каждой оппозицией следует аналогичная через 7 или 8 синодических периодов и очень похожая через 37 синодических периодов (79 лет). [8] В так называемой перигелической оппозиции Марс находится ближе всего к Солнцу и особенно близко к Земле: противостояния варьируются от примерно 0,68 а.е., когда Марс находится вблизи афелия, до всего около 0,37 а.е., когда Марс находится вблизи перигелия. [9]
Близкие подходы к Земле
[ редактировать ]Марс приближается к Земле ближе, чем любая другая планета, за исключением Венеры, находящейся ближе всего к ней: 56 миллионов километров — это самое близкое расстояние между Марсом и Землей, тогда как самое близкое расстояние между Марсом и Землей составляет 40 миллионов километров. Марс приближается к Земле ближе всего раз в два года, примерно во время своего противостояния, когда Земля проходит между Солнцем и Марсом. Сверхблизкие противостояния Марса происходят каждые 15–17 лет, когда мы проходим между Марсом и Солнцем примерно во время его перигелия (ближайшей точки к Солнцу на орбите). Минимальное расстояние между Землей и Марсом с годами уменьшалось, и в 2003 году минимальное расстояние составляло 55,76 миллиона км, что ближе, чем любое подобное столкновение почти за 60 000 лет (57 617 лет до нашей эры). Рекордное минимальное расстояние между Землей и Марсом в 2729 году составит 55,65 миллиона километров. В 3818 году рекорд составит 55,44 миллиона км, а расстояния будут продолжать уменьшаться примерно 24 000 лет. [10]
Историческое значение
[ редактировать ]До работы Иоганна Кеплера (1571–1630), немецкого астронома, преобладало убеждение, что Солнце и планеты вращаются вокруг Земли. В 1543 году Николай Коперник предположил, что все планеты вращаются вокруг Солнца, но его теория не давала очень удовлетворительных предсказаний и была по большей части проигнорирована. Когда Кеплер изучал наблюдения своего начальника Тихо Браге за положением Марса на небе в течение многих ночей, Кеплер понял, что орбита Марса не может быть кругом. После многих лет анализа Кеплер обнаружил, что орбита Марса, вероятно, представляет собой эллипс эллипса с Солнцем в одной из фокусных точек . Это, в свою очередь, привело Кеплера к открытию того, что все планеты вращаются вокруг Солнца по эллиптическим орбитам, причем Солнце находится в одной из двух фокусных точек. Это стало первым из трех законов движения планет Кеплера . [11] [12]
Точность/предсказуемость
[ редактировать ]С точки зрения всех, кроме самых требовательных, путь Марса прост. Уравнение в «Астрономических алгоритмах» , предполагающее невозмущенную эллиптическую орбиту, предсказывает время перигелия и афелия с ошибкой «несколько часов». [13] Использование орбитальных элементов для расчета этих расстояний соответствует фактическим средним значениям как минимум с пятью значащими цифрами. Формулы для расчета положения непосредственно на основе элементов орбиты обычно не предусматривают и не требуют поправок на влияние других планет. [14]
Для более высокого уровня точности необходимы возмущения планет. Они хорошо известны и, как полагают, смоделированы достаточно хорошо, чтобы обеспечить высокую точность. Это все органы, которые необходимо учитывать даже при многих сложных проблемах. Когда Альдо Витальяно рассчитал дату близкого сближения марсиан в далеком прошлом или будущем, он проверил потенциальный эффект, вызванный неопределенностями моделей пояса астероидов , запустив моделирование как с тремя крупнейшими астероидами, так и без них, и обнаружил, что эффекты были незначительными. .
Наблюдения улучшились, и технологии космической эры заменили старые методы. Э. Майлс Стэндиш писал: «Классические эфемериды на протяжении последних столетий полностью основывались на оптических наблюдениях: почти исключительно на времени прохождения меридианного круга. С появлением планетарного радара, миссий космических кораблей, РСДБ и т. д. ситуация для четырех внутренних планеты кардинально изменились». (8.5.1 стр. 10) Для DE405, созданного в 1995 году, оптические наблюдения были прекращены, и, как он писал, «начальные условия для четырех внутренних планет были скорректированы в первую очередь с учетом данных о дальности…» [15] Известно, что погрешность DE405 составляет около 2 км и сейчас составляет субкилометр. [16]
Хотя возмущения на Марсе со стороны астероидов вызвали проблемы, они также использовались для оценки масс некоторых астероидов. [17] Но улучшение модели пояса астероидов вызывает большую озабоченность у тех, кто требует или пытается получить эфемериды с высочайшей точностью. [18]
Орбитальные параметры
[ редактировать ]не более пяти значащих цифр Марса представлено В следующей таблице элементов орбиты . С таким уровнем точности цифры очень хорошо соответствуют элементам VSOP87 и расчетам, полученным на их основе, а также наилучшему приближению Стэндиша (из Лаборатории реактивного движения) за 250 лет и расчетам с использованием фактического положения Марса с течением времени.
| Расстояния и эксцентриситет | (В) | (миллион км) |
|---|---|---|
| Большая полуось | 1.5237 | 227.9 |
| Перигелий | 1.3814 | 206.7 |
| Афелион | 1.6660 | 249.2 |
| Средний [19] | 1.5303 | 228.9 |
| Окружность | 9.553 | 1429 |
| Самый близкий подход к Земле | 0.3727 | 55.76 |
| Самое дальнее расстояние от Земли | 2.675 | 400.2 |
| Эксцентриситет | 0.0934 | |
| Углы | (°) | |
| Наклон | 1.850 | |
| Период | (дней) | (годы) |
| орбитальный | 687.0 | 1.881 |
| Синодальный | 779.9 | 2.135 |
| Скорость | (км/с) | |
| Средний | 24.1 | |
| Максимум | 26.5 | |
| Минимум | 22.0 | |
Ссылки
[ редактировать ]- ^ Саймон, Дж.Л.; Бретаньон, П.; Чапрон, Дж.; Шапрон-Тузе, М.; Франку, Г.; Ласкар, Дж. (февраль 1994 г.). «Численные выражения для формул прецессии и средних элементов для Луны и планет». Астрономия и астрофизика . 282 (2): 663–683. Бибкод : 1994A&A...282..663S .
- ^ Жан Меус, Астрономические формулы для калькуляторов . (Ричмонд, Вирджиния: Willmann-Bell, 1988) 99. Элементы Ф. Е. Росса.
- ^ В эфемеридных сутках 86 400 секунд. Продолжительность сидерического и аномалистического года составляет 686,980 и 686,996 дней соответственно. (Разница около 20 минут). Сидерический год — это время, необходимое для обращения вокруг Солнца относительно фиксированной системы отсчета. Точнее, сидерический год — это один из способов выразить скорость изменения средней долготы в один момент относительно фиксированного равноденствия. Расчет показывает, за какое время долгота изменится на 360 градусов с заданной скоростью.Аномалистический год — это промежуток времени между последовательными прохождениями перигелия или афелия. Его можно рассчитать так же, как и звездный год, но используется средняя аномалия.
- ^ Джин Миус, Астрономические алгоритмы (Ричмонд, Вирджиния: Willmann-Bell, 1998) 238. Формула Рамануджана достаточно точна.
- ^ Уильямс, Дэвид (2018). «Информационный бюллетень о Марсе» . Центр космических полетов имени Годдарда НАСА. Архивировано из оригинала 17 марта 2020 года . Проверено 22 марта 2020 г. ; Средняя аномалия (градусы) 19,412 = (Средняя долгота (градусы) 355,45332) – (Долгота перигелия (градусы) 336,04084)
 В данную статью включен текст из этого источника, находящегося в свободном доступе .
В данную статью включен текст из этого источника, находящегося в свободном доступе . - ^ «МарсДист» . Архивировано из оригинала 7 сентября 2007 г. Проверено 20 июля 2007 г. Расстояние до Марса и эксцентриситет с использованием SOLEX . Его создатель Альдо Витальяно.
- ^ Синодический период можно рассчитать как 1/(1/p-1/q), где p и q — меньший и больший сидерический периоды.
- ^ Синодический период Марса на 92,9 дня длиннее его сидерического периода, составляющего 687,0 дней. Затем он переместился вперед на 92,9/687,0 раз на 360, или 48,7 градусов. После семи противостояний он продвинулся вперед на 341 градус, а после восьми — на 390 градусов; в первом случае его долгота отличается от одного оборота на 19°, а во втором на 30°. Так что ситуации тогда будут схожими. Подобные расчеты показывают, что долгота меняется всего на 2° после 37 противостояний.
- ^ Шиэн, Уильям (2 февраля 1997 г.). «Приложение 1: Противостояния Марса, 1901–2035 гг.» . Планета Марс: история наблюдений и открытий . Издательство Университета Аризоны. Архивировано из оригинала 25 июня 2010 года . Проверено 30 января 2010 г.
- ^ Меус, Жан (март 2003 г.). «Когда Марс последний раз был так близко?» (PDF) . Планетарий : 13.
- ^ Карр, Майкл Х.; Малин, Майкл С .; Белтон, Майкл Дж. С. (27 июля 2018 г.). «Марс» . Британская онлайн-энциклопедия . п. 2.
- ^ Уильям Шиэн, Планета Марс: история наблюдений и открытий (Тусон, Аризона: The University of Arizona Press, 1996), Глава 1
- ^ Миус (1998), стр. 269–270.
- ^ см., например, Simon et al. (1994) с. 681
- ^ Стэндиш и Уильямс (2012). «ГЛАВА 8: Орбитальные эфемериды Солнца, Луны и планет» (PDF) . Версия Пояснительного приложения 2012 г.
- ^ Как отмечается в меморандуме Лаборатории реактивного движения 2008 года относительно DE421: «Теперь известно, что ошибка в орбитах Земли и Марса в DE405 составляет около 2 км, что было хорошей точностью в 1997 году, но намного хуже, чем нынешняя точность субкилометра». Фолкнер; и др. (2008). «Планетарные и лунные эфемериды DE421» (PDF) . Межофисный меморандум JPL IOM 343.R-08-003 . п. 1
- ^ «Астероид». Британская энциклопедия . Британская энциклопедия Интернет. Британская энциклопедия Inc., 2014. Интернет. 19 августа 2014 г. http://www.britanica.com/EBchecked/topic/39730/asteroid.
- ^ «Неопределенность орбиты Марса для годового прогноза составляет около 300 м, как это требуется для миссии Марсианской научной лаборатории, но быстро растет в течение времени до ипосле периода наблюдения космического корабля из-за влияния астероидов с орбитами, близкими к орбите Марса. Прогнозируемая орбита и неопределенность во многом зависят от используемой модели астероида. " Фолкнер; и др. (2010). «Неопределенности в планетарных эфемеридах Лаборатории реактивного движения» (PDF) . Материалы путешествий . п. 43.
- ^ Среднее расстояние по времени. Постоянный член в VSOP87. Оно соответствует среднему значению многих коротких равных промежутков времени.