Скрытый аттрактор
В этой статье есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
В теории бифуркаций ограниченное колебание , возникающее без потери устойчивости стационарного множества, называется скрытым колебанием . В нелинейной теории управления рождение скрытого колебания в стационарной системе управления с ограниченными состояниями означает пересечение границы в области параметров, где локальная устойчивость стационарных состояний влечет за собой глобальную устойчивость (см., например, гипотезу Калмана ). . Если скрытое колебание (или совокупность таких скрытых колебаний, заполняющих компактное подмножество фазового пространства динамической системы ) притягивает все близлежащие колебания, то оно называется скрытым аттрактором . Для динамической системы с единственной точкой равновесия, которая является глобально привлекательной, рождение скрытого аттрактора соответствует качественному изменению поведения от моностабильности к бистабильности. В общем случае динамическая система может оказаться мультистабильной и иметь сосуществующие локальные аттракторы в фазовом пространстве . В то время как тривиальные аттракторы, т.е. устойчивые точки равновесия , можно легко найти аналитически или численно, поиск периодических и хаотических аттракторов может оказаться сложной задачей (см., например, вторую часть 16-й проблемы Гильберта ).
Классификация аттракторов на скрытые и самовозбуждающиеся.
[ редактировать ]Чтобы идентифицировать локальный аттрактор в физическом или численном эксперименте, необходимо выбрать начальное состояние системы в зоне притяжения аттрактора и наблюдать, как состояние системы, начиная с этого начального состояния, после переходного процесса визуализирует аттрактор. Классификация аттракторов на скрытые или самовозбуждающиеся отражает трудности выявления бассейнов притяжения и поиска локальных аттракторов в фазовом пространстве .
Определение . [1] [2] [3] Аттрактор называется скрытым аттрактором, если его бассейн притяжения не пересекается с некоторой открытой окрестностью точек равновесия; в противном случае его называют самовозбуждающимся аттрактором.
Классификация аттракторов на скрытые и самовозбуждающиеся была введена Г. Леоновым и Н. Кузнецовым в связи с открытием скрытого аттрактора Чуа. [4] [5] [6] [7] впервые в 2009 году. Точно так же произвольное ограниченное колебание, не обязательно имеющее открытую окрестность в качестве зоны притяжения в фазовом пространстве, классифицируется как самовозбуждающееся или скрытое колебание.

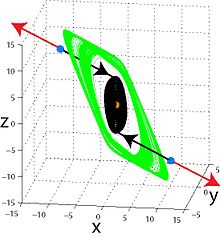

Самовозбуждающиеся аттракторы
[ редактировать ]Для самовозбуждающегося аттрактора его бассейн притяжения связан с неустойчивым равновесием, поэтому самовозбуждающиеся аттракторы можно найти численно с помощью стандартной вычислительной процедуры, в которой после переходного процесса определяется траектория, начинающаяся в окрестности неустойчивое равновесие, притягивается к состоянию колебания и затем отслеживает его (см., напр., автоколебаний процесс ). Таким образом, самовозбуждающиеся аттракторы, даже сосуществующие в случае мультистабильности , легко выявляются и визуализируются численно. В системе Лоренца для классических параметров аттрактор самовозбуждается относительно всех существующих равновесий и может быть визуализирован любой траекторией из их окрестностей; однако при некоторых других значениях параметров существуют два тривиальных аттрактора, сосуществующих с хаотическим аттрактором, который является самовозбуждающимся только по отношению к нулевому равновесию. Классические аттракторы в динамических системах Ван дер Поля , Белуосова–Жаботинского , Рёсслера , Чуа , Энона являются самовозбуждающимися.
Высказано предположение, что ляпуновская размерность самовозбуждающегося аттрактора не превышает ляпуновской размерности одного из неустойчивых состояний равновесия, неустойчивое многообразие которого пересекается с тазом притяжения и визуализирует аттрактор. [8]
Скрытые аттракторы
[ редактировать ]Скрытые аттракторы имеют бассейны притяжения, не связанные с равновесиями и «спрятанные» где-то в фазовом пространстве. Например, скрытые аттракторы являются аттракторами в системах без равновесия: например, во вращающихся электромеханических динамических системах с эффектом Зоммерфельда (1902 г.), в системах только с одним устойчивым равновесием: например, контрпримеры к гипотезе Айзермана (1949 г.) и гипотезе Калмана (1957) о моностабильности нелинейных систем управления. Одной из первых смежных теоретических задач является вторая часть 16-й проблемы Гильберта о числе и взаимном расположении предельных циклов в двумерных полиномиальных системах, где вложенные устойчивые предельные циклы являются скрытыми периодическими аттракторами. Понятие скрытого аттрактора стало катализатором открытия скрытых аттракторов во многих прикладных динамических моделях. [1] [9] [10]
В общем, проблема со скрытыми аттракторами заключается в том, что не существует общих простых методов отслеживания или прогнозирования таких состояний для динамики системы (см., например, [11] ). Если для двумерных систем скрытые колебания можно исследовать аналитическими методами (см., например, результаты по второй части 16-й задачи Гильберта ), то для исследования устойчивости и колебаний в сложных нелинейных многомерных системах часто применяют численные методы. .В многомерном случае интегрирование траекторий со случайными начальными данными вряд ли обеспечит локализацию скрытого аттрактора, поскольку зона притяжения может быть очень мала, а сама размерность аттрактора может быть много меньше размерности рассматриваемого аттрактора. система.Поэтому для численной локализации скрытых аттракторов в многомерном пространстве необходима разработка специальных аналитико-численных вычислительных процедур, [1] [12] [8] которые позволяют выбрать начальные данные в области притяжения скрытого колебания (не содержащей окрестностей равновесий), а затем выполнить траекторный расчет.Существуют соответствующие эффективные методы, основанные на гомотопия и численное продолжение : строится последовательность подобных систем такая, чтодля первой (стартовой) системы исходные данные для численного расчета осциллирующего решения(стартовое колебание) можно получить аналитически, а затем численно проследить трансформацию этого стартового колебания при переходе от одной системы к другой.
Теория скрытых колебаний
[ редактировать ]
Классификация аттракторов на самовозбуждающиеся и скрытые была фундаментальной.предпосылкой возникновения теории скрытых колебаний, которая представляет собойсовременное развитие теории колебаний Андронова. Это ключ к определению точных границ глобальной стабильности. части которых Н. Кузнецов относит к тривиальным (т. е. определяемымлокальными бифуркациями) или скрытыми (т. е. определяемыми нелокальными бифуркациями)и рождением скрытых колебаний). [13] [14]
Ссылки
[ редактировать ]- ↑ Перейти обратно: Перейти обратно: а б с Леонов Г.А.; Кузнецов Н.В. (2013). «Скрытые аттракторы в динамических системах. От скрытых колебаний в задачах Гильберта-Колмогорова, Айзермана и Калмана к скрытому хаотическому аттрактору в схемах Чуа». Международный журнал бифуркации и хаоса в прикладных науках и технике . 23 (1): 1330002–219. Бибкод : 2013IJBC...2330002L . дои : 10.1142/S0218127413300024 .
- ^ Брагин В.О.; Вагайцев В.И.; Кузнецов Н.В.; Леонов Г.А. (2011). «Алгоритмы поиска скрытых колебаний в нелинейных системах. Гипотезы Айзермана и Калмана и схемы Чуа» (PDF) . Международный журнал компьютерных и системных наук . 50 (5): 511–543. дои : 10.1134/S106423071104006X . S2CID 21657305 .
- ^ Леонов Г.А.; Кузнецов Н.В.; Мокаев, ТН (2015). «Гомоклинические орбиты, самовозбуждающиеся и скрытые аттракторы в лоренцеподобной системе, описывающей конвективное движение жидкости». Специальные темы Европейского физического журнала . 224 (8): 1421–1458. arXiv : 1505.04729 . doi : 10.1140/epjst/e2015-02470-3 . S2CID 119227870 .
- ^ Кузнецов Н.В.; Леонов Г.А.; Вагайцев В.И. (2010). «Аналитико-численный метод локализации аттрактора обобщенной системы Чуа» . Тома трудов МФБ . 43 (11): 29–33. дои : 10.3182/20100826-3-TR-4016.00009 .
- ^ Леонов Г.А.; Вагайцев В.И.; Кузнецов Н.В. (2011). «Локализация скрытых аттракторов Чуа» (PDF) . Письма по физике . 375 (23): 2230–2233. Бибкод : 2011PhLA..375.2230L . дои : 10.1016/j.physleta.2011.04.037 .
- ^ Леонов Г.А.; Вгайцев В.И.; Кузнецов Н.В. (2012). «Скрытый аттрактор в гладких системах Чуа» (PDF) . Физика Д. 241 (18): 1482–1486. Бибкод : 2012PhyD..241.1482L . дои : 10.1016/j.physd.2012.05.016 .
- ↑ Перейти обратно: Перейти обратно: а б Кузнецов Н.В.; Леонов Г.А.; Мокаев, Теннесси; Прасад, А.; Шримали, доктор медицинских наук (2018). «Конечная размерность Ляпунова и скрытый аттрактор системы Рабиновича». Нелинейная динамика . 92 (2): 267–285. arXiv : 1504.04723 . дои : 10.1007/s11071-018-4054-z . S2CID 54706479 .
- ^ Кузнецов Н.В.; Леонов Г.А. (2014). «Скрытые аттракторы в динамических системах: системы без равновесия, мультистабильность и сосуществующие аттракторы». Тома трудов МФБ (Материалы Всемирного конгресса МФБ) . 47 (3): 5445–5454. дои : 10.3182/20140824-6-ZA-1003.02501 .
- ^ Кузнецов Н.В.; Леонов Г.А.; Юлдашев, М.В.; Юлдашев, Р.В. (2017). «Скрытые аттракторы в динамических моделях схем фазовой автоподстройки частоты: ограничения моделирования в MATLAB и SPICE» . Коммуникации в нелинейной науке и численном моделировании . 51 : 39–49. Бибкод : 2017CNSNS..51...39K . дои : 10.1016/j.cnsns.2017.03.010 .
- ^ Чен, Г.; Кузнецов Н.В.; Леонов Г.А.; Мокаев, ТН (2015). «Скрытые аттракторы на одном пути: системы Глуховского-Должанского, Лоренца и Рабиновича». Международный журнал бифуркации и хаоса в прикладных науках и технике . 27 (8): ст. число 1750115.arXiv : 1705.06183 . дои : 10.1142/S0218127417501152 . S2CID 21425647 .
- ^ Кузнецов Н.В. (2020). «Теория скрытых колебаний и устойчивость систем управления» (PDF) . Международный журнал компьютерных и системных наук . 59 (5): 647–668. дои : 10.1134/S1064230720050093 . S2CID 225304463 .
- ^ Кузнецов Н.В.; Мокаев, Теннесси; Кузнецова О.А.; Кудряшова, Е.В. (2020). «Система Лоренца: скрытая граница практической устойчивости и ляпуновская размерность» . Нелинейная динамика . 102 (2): 713–732. дои : 10.1007/s11071-020-05856-4 .
Книги
[ редактировать ]- Хаотические системы с мультистабильностью и скрытыми аттракторами (ред.: Ван, Кузнецов, Чен), Springer, 2021 ( doi:10.1007/978-3-030-75821-9 )
- Нелинейные динамические системы с самовозбуждающимися и скрытыми аттракторами (ред.: Фам, Вайдьянатан, Волос и др.), Springer, 2018 ( doi:10.1007/978-3-319-71243-7 )
Избранные лекции
[ редактировать ]- Н.Кузнецов, Приглашенная лекция Теория скрытых колебаний и устойчивость динамических систем , Межд. Семинар по прикладной математике, Чехия, 2021 г.
- Пленарная лекция премии Афраймовича: Кузнецов Н.В. Теория скрытых колебаний и устойчивость динамических систем. Межд. Конференция «Нелинейная динамика и сложность», 2021 г.