Диаграмма состояний

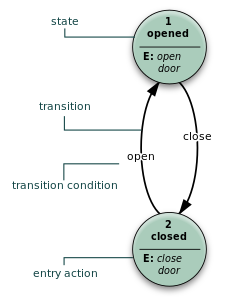
Диаграмма состояний используется в информатике и смежных областях для описания поведения систем. Диаграммы состояний требуют, чтобы система состояла из конечного числа состояний . Иногда это действительно так, а иногда это разумная абстракция . Существует множество форм диаграмм состояний, которые незначительно отличаются и имеют разную семантику .

Обзор

дают абстрактное описание системы поведения Диаграммы состояний . Такое поведение анализируется и представляется серией событий, которые могут произойти в одном или нескольких возможных состояниях. При этом «каждая диаграмма обычно представляет объекты одного класса и отслеживает различные состояния своих объектов в системе». ^[1]

Диаграммы состояний можно использовать для графического представления конечных автоматов (также называемых конечными автоматами). Это было введено Клодом Шенноном и Уорреном Уивером в их книге 1949 года «Математическая теория коммуникации» . Другой источник — Тейлор Бут в его книге 1967 года «Последовательные машины и теория автоматов» . Другое возможное представление — таблица переходов состояний .

Ориентированный граф

Классической формой диаграммы состояний конечного автомата (КА) является ориентированный граф со следующими элементами (Q, Σ, Z, δ, q0 _, F): ^[2]^[3]

Вершины Q : конечный набор состояний, обычно представленный кружками и помеченный уникальными символами-обозначениями или словами, написанными внутри них.
Входные символы Σ : конечный набор входных символов или обозначений.
Выходные символы Z : конечный набор выходных символов или обозначений.

Выходная функция ω представляет собой отображение упорядоченных пар входных символов и состояний на выходные символы, математически обозначаемые ω : Σ × Q → Z. как

Края δ : представляют собой переходы из одного состояния в другое, вызванные входными данными (обозначаются их символами, нарисованными на краях). Ребро обычно изображается в виде стрелки, направленной от текущего состояния к следующему. Это отображение описывает переход состояний, вызванный вводом. Математически это записывается как δ : Q × Σ → Q , поэтому δ (функция перехода) в определении FA задается как парой вершин, соединенных ребром, так и символом на ребре в диаграмме, представляющей этот FA. . Пункт δ(q, a) = p в определении FA означает, что из состояния с именем q под входным символом a в этой машине происходит переход в состояние p . На диаграмме, представляющей этот FA, это представлено ребром, помеченным точкой , ведущей от вершины, помеченной q, к вершине, помеченной p .
Начальное состояние q ₀ : (не показано в примерах ниже). Начальное состояние q ₀ ∈ Q обычно изображается стрелкой без начала координат, указывающей на состояние. В старых текстах ^[2]^[4] начальное состояние не отображается и должно быть выведено из текста.
Принимающее состояние(я) F : Если используется, например, для принятия автоматов, F ∈ Q является принимающим состоянием . Обычно его рисуют в виде двойного круга. Иногда состояния принятия функционируют как « финальные » состояния (остановка, ловушка). ^[3]

Для детерминированного конечного автомата (DFA), недетерминированного конечного автомата (NFA), обобщенного недетерминированного конечного автомата (GNFA) или машины Мура вход обозначается на каждом ребре. Для машины Мили вход и выход обозначаются на каждом ребре, разделенные косой чертой «/»: «1/0» обозначает изменение состояния при обнаружении символа «1», вызывающее вывод символа «0». Для машины Мура вывод состояния обычно записывается внутри круга состояния, а также отделяется от обозначения состояния косой чертой «/». Есть также варианты, сочетающие эти два обозначения.

Например, если состояние имеет несколько выходов (например, «a= двигатель вращается против часовой стрелки = 1, b = сигнальная лампа неактивна = 0»), диаграмма должна отражать это: например, «q5/1,0» обозначает состояние q5 с помощью выходы а=1, б=0. Этот указатель будет написан внутри кружка штата.

Пример: DFA, NFA, GNFA или машина Мура.

S1 _а и S2 _, — состояния S1 _— принимающее состояние или конечное . Каждое ребро помечено входными данными. В этом примере показан акцептор для двоичных чисел, содержащих четное количество нулей.

Пример: Мучнистая машина

S0 , S1 _и состояниями S2 _{являются} . Каждое ребро помечено буквой « j / k », где j — вход, а k — выход.

Диаграмма состояний простого автомата Мили

Диаграмма состояний Хареля

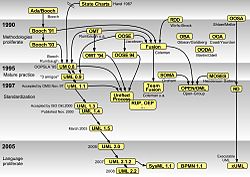
диаграммы состояний Хареля, ^[5] изобретенные учёным-компьютерщиком Дэвидом Харелом , получают широкое распространение, поскольку их вариант стал частью унифицированного языка моделирования (UML). ^{[ нужен неосновной источник ]} Тип диаграммы позволяет моделировать сверхгосударства , ортогональные регионы и действия как часть государства.

Классические диаграммы состояний требуют создания отдельных узлов для каждой допустимой комбинации параметров, определяющих состояние. Для всех систем, кроме самых простых, это может привести к очень большому количеству узлов и переходов между узлами ( взрыв состояний и переходов ), что снижает читаемость диаграммы состояний. С помощью диаграмм состояний Harel можно моделировать несколько кросс-функциональных диаграмм состояний внутри диаграммы состояний. Каждый из этих межфункциональных конечных автоматов может выполнять внутренний переход, не затрагивая другие конечные автоматы. Текущее состояние каждого межфункционального конечного автомата определяет состояние системы. Диаграмма состояний Хареля эквивалентна диаграмме состояний, но улучшает ее читаемость.

Альтернативная семантика

Существуют и другие наборы семантики для представления диаграмм состояний. Например, существуют инструменты для моделирования и проектирования логики встроенных контроллеров. ^[6] Эти диаграммы, как и оригинальные конечные автоматы Хареля, ^[7] поддерживать иерархически вложенные состояния, ортогональные области, действия состояний и действия перехода. ^[8]

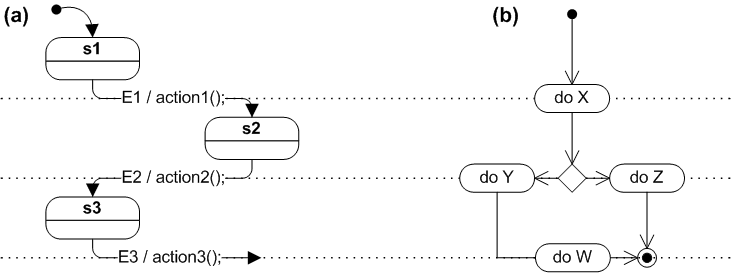
Диаграммы состояний и блок-схемы

Новички в формализме конечных автоматов часто путают диаграммы состояний с блок-схемами . На рисунке ниже показано сравнение диаграммы состояний с блок-схемой. Конечный автомат (панель (а)) выполняет действия в ответ на явные события. Напротив, блок-схема (панель (b)) автоматически переходит от узла к узлу после завершения действий. ^[9]

Диаграмма состояний (а) и блок-схема (б)

Узлы блок-схем являются ребрами индуцированного графа состояний. Причина в том, что каждый узел блок-схемы представляет собой команду программы. Команда программы – это действие, которое необходимо выполнить. Команда не является состоянием, но при применении к состоянию программы вызывает переход в другое состояние.

Более подробно, листинг исходного кода представляет собой граф программы. Выполнение графа программы (синтаксический анализ и интерпретация) приводит к созданию графа состояний. Таким образом, каждый граф программы порождает граф состояний. Преобразование графа программы в связанный с ним граф состояний называется «развертыванием» графа программы.

Граф программы представляет собой последовательность команд. Если переменных не существует, то состояние состоит только из счетчика программ, который отслеживает местоположение программы во время выполнения (какая следующая команда будет применена).

Перед выполнением команды счетчик программы находится в некоторой позиции (состоянии до выполнения команды). Выполнение команды переводит счетчик программы на следующую команду. Поскольку счетчик программы — это все состояние, выполнение команды изменило состояние. Таким образом, сама команда соответствует переходу между двумя состояниями.

Теперь рассмотрим полный случай, когда переменные существуют и на них влияют выполняемые команды программы. Мало того, что счетчик программы изменяется в разных местах счетчика программы, но переменные также могут изменять значения в результате выполнения команд. Следовательно, даже если мы повторно обратимся к некоторой команде программы (например, в цикле), это не означает, что программа находится в том же состоянии.

В предыдущем случае программа находилась бы в том же состоянии, поскольку все состояние — это всего лишь счетчик программ. Таким образом, если программа указывает на одну и ту же позицию (следующую команду), достаточно указать, что мы находимся в том же состоянии. Однако если состояние включает в себя переменные, которые меняют значение, мы можем находиться в одном и том же месте программы с разными значениями переменных, то есть в другом состоянии в пространстве состояний программы. Термин «развертывание» происходит от умножения мест при создании графа состояний из графа программы.

Самопереход — это переход, при котором начальное и конечное состояния совпадают.

Типичным примером является цикл do, увеличивающий некоторый счетчик до тех пор, пока он не переполнится и снова не станет равным 0. Хотя цикл do итеративно выполняет одну и ту же команду приращения, его пространство состояний представляет собой не цикл, а строку. Это происходит из-за того, что состояние является местоположением программы (здесь циклично) в сочетании со значением счетчика, которое строго увеличивается (до переполнения). Таким образом, различные состояния посещаются последовательно, пока не произойдет переполнение. После переполнения счетчик снова становится равным 0, поэтому исходное состояние возвращается в пространство состояний, замыкая цикл в пространстве состояний (при условии, что счетчик был инициализирован на 0).

На рисунке выше предпринята попытка показать эту смену ролей путем совмещения дуг диаграмм состояний с этапами обработки блок-схемы.

Блок-схему можно сравнить со сборочной линией на производстве, поскольку она описывает ход выполнения некоторой задачи от начала до конца (например, преобразование входного исходного кода в выходной объектный код компилятора). Государственная машина обычно не имеет представления о таком развитии. Показанный выше пример конечного автомата двери находится не на более продвинутой стадии в «закрытом» состоянии, чем в «открытом». Скорее, он просто по-разному реагирует на события открытия/закрытия. Состояние в конечном автомате — это эффективный способ задания поведения, а не этапа обработки.

Другие расширения

Интересное расширение — позволить дугам переходить из любого количества состояний в любое количество состояний. Это имеет смысл только в том случае, если системе разрешено находиться в нескольких состояниях одновременно, что означает, что отдельное состояние описывает только состояние или другой частичный аспект общего, глобального состояния. Полученный формализм известен как сеть Петри .

Другое расширение позволяет интегрировать блок-схемы в диаграммы состояний Harel. Это расширение поддерживает разработку программного обеспечения, которое управляется как событиями, так и рабочими процессами.

См. также

Дэвид Харел
DRAKON
SCXML — язык XML, который обеспечивает общую среду выполнения на основе конечного автомата на основе диаграмм состояний Harel.
Конечный автомат UML
YAKINDU Statechart Tools — это программное обеспечение для моделирования диаграмм состояний (диаграммы состояний Харела, машин Мили, машин Мура), моделирования и генерации исходного кода.

Ссылки

^ Архивный указатель на Wayback Machine
^ Перейти обратно: ^а ^б Тейлор Бут (1967) Теория последовательных машин и автоматов , Джон Уайли и сыновья, Нью-Йорк.
^ Перейти обратно: ^а ^б Джон Хопкрофт и Джеффри Уллман (1979) «Введение в теорию автоматов, языки и вычисления» , издательство Addison-Wesley Publishing Company, Reading Mass, ISBN 0-201-02988-X
^ Эдвард Дж. МакКласки , Введение в теорию переключающих цепей, McGraw-Hill, 1965.
^ Дэвид Харел , Диаграммы состояний: визуальный формализм для сложных систем. Наука компьютерного программирования , 8 (3): 231–274, июнь 1987 г.
^ Тивари, А. (2002). Формальная семантика и методы анализа для Simulink Stateflow.
^ Харель, Д. (1987). Визуальный формализм для сложных систем. Наука компьютерного программирования, 231–274.
^ Алур Р., Канаде А., Рамеш С. и Шашидхар К.К. (2008). Символьный анализ для улучшения охвата моделирования моделей Simulink/Stateflow. Международная конференция по встраиваемому программному обеспечению (стр. 89–98). Атланта, Джорджия: ACM.
^ Самек, Миро (2008). Практические диаграммы состояний UML на C/C++, второе издание: событийно-ориентированное программирование для встраиваемых систем . Ньюнес. п. 728. ИСБН 978-0-7506-8706-5 .

Внешние ссылки

Введение в диаграммы конечных автоматов UML 2 Скотта В. Эмблера
Рекомендации по диаграммам конечных автоматов UML 2 , Скотт В. Эмблер
Intelliwizard — UML StateWizard — прекращенная платформа и инструмент для динамического моделирования/разработки UML, работающие в популярных IDE под лицензией с открытым исходным кодом.
YAKINDU Statechart Tools — инструмент с открытым исходным кодом для спецификации и разработки реактивных, управляемых событиями систем с помощью конечных автоматов .
Понимание и использование конечных автоматов MATLAB Tech Talks о конечных автоматах
FSM: генерация конечных автоматов с открытым исходным кодом на Java, Александр Сахаров FSM
scxmlcc Эффективный конечный автомат scxml для компилятора C++.
SMC: компилятор конечного автомата с открытым исходным кодом, который генерирует FSM для многих языков, таких как C, Python, Lua, Scala, PHP, Java, VB и т. д. SMC

[1] Архивный указатель на Wayback Machine

[Boo67-2] Перейти обратно: ^а ^б Тейлор Бут (1967) Теория последовательных машин и автоматов , Джон Уайли и сыновья, Нью-Йорк.

[HoU79-3] Перейти обратно: ^а ^б Джон Хопкрофт и Джеффри Уллман (1979) «Введение в теорию автоматов, языки и вычисления» , издательство Addison-Wesley Publishing Company, Reading Mass, ISBN 0-201-02988-X

[McC65-4] Эдвард Дж. МакКласки , Введение в теорию переключающих цепей, McGraw-Hill, 1965.

[Har87-5] Дэвид Харел , Диаграммы состояний: визуальный формализм для сложных систем. Наука компьютерного программирования , 8 (3): 231–274, июнь 1987 г.

[6] Тивари, А. (2002). Формальная семантика и методы анализа для Simulink Stateflow.

[7] Харель, Д. (1987). Визуальный формализм для сложных систем. Наука компьютерного программирования, 231–274.

[8] Алур Р., Канаде А., Рамеш С. и Шашидхар К.К. (2008). Символьный анализ для улучшения охвата моделирования моделей Simulink/Stateflow. Международная конференция по встраиваемому программному обеспечению (стр. 89–98). Атланта, Джорджия: ACM.

[Practical_UML_Statecharts_in_C/C++,_Second_Edition:_Event-Driven_Programming_for_Embedded_Systems-9] Самек, Миро (2008). Практические диаграммы состояний UML на C/C++, второе издание: событийно-ориентированное программирование для встраиваемых систем . Ньюнес. п. 728. ИСБН 978-0-7506-8706-5 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]