Роза (математика)

Розы, заданные синусоидой $r = cos(kθ)$ для различных рациональных нумерованных значений угловой частоты $k = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ n / d ⁠$ .
Розы, заданные $r = sin(kθ),$ представляют собой повороты этих роз на четверть периода синусоиды в направлении против часовой стрелки вокруг полюса (начала координат). Для правильного математического анализа $k$ должно быть выражено в неприводимой форме.

В математике представляет собой синусоиду кривая «роза» или «родонея» , определяемую косинусом или синусоидой без фазового угла и отображаемую в полярных координатах . Кривые розы или «родонея» были названы итальянским математиком, изучавшим их, Гвидо Гранди между 1723 и 1728 годами. ^{[ 1 ]}

Общий обзор

Спецификация

Роза — это набор точек в полярных координатах, заданных полярным уравнением. ^{[ 2 ]}

r=a\cos(k\theta )

или в декартовых координатах с использованием параметрических уравнений

{\begin{aligned}x&=r\cos(\theta )=a\cos(k\theta )\cos(\theta )\\y&=r\sin(\theta )=a\cos(k\theta )\sin(\theta )\end{aligned}}

Розы также можно указать с помощью функции синуса. ^{[ 3 ]} С

\sin(k\theta )=\cos \left(k\theta -{\frac {\pi }{2}}\right)=\cos \left(k\left(\theta -{\frac {\pi }{2k}}\right)\right)

.

Таким образом, роза, заданная $r = a sin(kθ)$ , идентична розе, заданной $r = a cos(kθ),$ повернутой против часовой стрелки на $⁠ π / 2 k ⁠$ радиан, что составляет четверть периода любой синусоиды.

Поскольку они задаются с использованием функции косинуса или синуса, розы обычно выражаются в виде графиков полярных координат (а не декартовых координат ) синусоид, которые имеют угловую частоту k $и$ амплитуду a которые $,$ определяют радиальную координату $r$ с учетом полярного угла $θ$ ( хотя, когда $k$ является рациональным числом , роза-кривая может быть выражена в декартовых координатах, поскольку они могут быть заданы как алгебраические кривые. ^{[ 4 ]}).

Общие свойства

Художественное изображение роз с различными настройками параметров.

Розы напрямую связаны со свойствами задающих их синусоидов.

Лепестки

Графы роз состоят из лепестков . Лепесток — это форма, образованная графиком полупериода синусоиды, характеризующей розу. (Цикл — это часть синусоиды, имеющая один период T = ⁠ 2 π / k ⁠ длиной и состоит из положительного полупериода, непрерывного набора точек, где r ≥ 0 , и ⁠ T / 2 ⁠ = ⁠ π / k ⁠ длинный, а отрицательный полупериод — это другая половина, где r ≤ 0. )
- Форма каждого лепестка одинакова, поскольку графики полупериодов имеют одинаковую форму. Форма задается положительным полупериодом с гребнем в точке $(a,0),$ заданным $r = a cos(kθ)$ (который ограничен интервалом углов $— ⁠ Т / 4 ⁠ \leq θ \leq ⁠ Т / 4 ⁠$ ). Лепесток симметричен относительно полярной оси. Все остальные лепестки представляют собой вращения этого лепестка вокруг полюса, в том числе и для роз, заданных функцией синуса с одинаковыми значениями $a$ и $k$ . ^{[ 5 ]}
- В соответствии с правилами построения точек в полярных координатах, точка в отрицательном полупериоде не может быть нанесена под ее полярным углом, поскольку ее радиальная координата $r$ отрицательна. Точка строится путем добавления $π$ радиан к полярному углу с радиальной координатой $| р |$ . Таким образом, на графике розы положительные и отрицательные полупериоды могут совпадать. вписаны розы $Кроме того, в круг r = a$ .
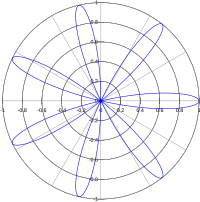
- Когда период $T$ синусоиды меньше или равен $4 π$ , форма лепестка представляет собой одинарный замкнутый контур. Одиночная петля образуется, потому что угловой интервал для полярного графика составляет $2 π$ , а угловая ширина полупериода меньше или равна $2 π$ . Когда $T > 4 π$ (или $| k | < ⁠ 1 / 2 ⁠$ ) график полупериода можно рассматривать как спиральный исходящий от полюса более чем один оборот вокруг полюса, пока график не достигнет вписанного круга, где он возвращается по спирали обратно к полюсу, пересекаясь и образуя один или больше петель по пути. Следовательно, каждый лепесток образует две петли при $4 π < T \leq 8 π$ (или $⁠ 1 / 4 ⁠ \leq | к | < ⁠ 1/2 8 ⁠ ($ ), три петли при $< π \leq T 12 π$ или $⁠ 1 / 6 ⁠ \leq | к | < ⁠ 1 / 4 ⁠$ ) и т. д. Розы только с одним лепестком с множеством петель наблюдаются при $k = ⁠ 1 / 3 ⁠, ⁠ 1 / 5 ⁠, ⁠ 1/7 т. д. (См . ⁠ и$ рисунок во вводной части.)
- Лепестки розы не будут пересекаться друг с другом, если угловая частота $k$ является ненулевым целым числом; в противном случае лепестки пересекаются друг с другом.

Симметрия

Все розы демонстрируют одну или несколько форм симметрии из-за лежащих в их основе симметричных и периодических свойств синусоид.

Роза, заданная как $r = a cos(kθ),$ симметрична относительно полярной оси (линия $θ = 0$ ) из-за тождества $a cos(kθ) = a cos(- kθ),$ что делает розы, заданные двумя полярными уравнениями, совпадение.

Роза, заданная как $r = a sin(kθ),$ симметрична относительно вертикальной линии $θ = ⁠ π / 2 ⁠$ из-за тождества $a sin(kθ) = a sin(π - kθ)$ , которое делает розы, заданные двумя полярными уравнениями, совпадающими.

Лишь некоторые розы симметричны относительно полюса.

Отдельные лепестки симметричны относительно линии, проходящей через полюс и вершину лепестка, что отражает симметрию полупериода базовой синусоиды. Розы, состоящие из конечного числа лепестков, по определению вращательно-симметричны , поскольку каждый лепесток имеет одинаковую форму, а последующие лепестки повернуты примерно на один и тот же угол вокруг полюса.

Розы с ненулевыми целочисленными значениями $k$

Если $k$ — целое число, отличное от нуля, кривая будет иметь форму розы с $2 k$ лепестками, если $k$ четное, и $k$ лепестками, если $k$ нечетное. ^{[ 6 ]} Свойства этих роз представляют собой частный случай роз с угловыми частотами $k$ , которые являются рациональными числами, обсуждаемыми в следующем разделе этой статьи.

Роза вписана в круг $r = a$ , соответствующий радиальной координате всех ее вершин.

Поскольку график полярных координат ограничен полярными углами от 0 до $2 π$ , существуют $⁠ 2 π / T ⁠ = k$ циклов, отображенных на графике. Никаких дополнительных точек наносить не требуется, поскольку радиальная координата при $θ = 0$ имеет то же значение при $θ = 2 π$ (которые представляют собой гребни для двух разных положительных полупериодов для роз, определяемых функцией косинуса).

Когда k четное (и ненулевое), роза состоит из 2 k лепестков, по одному на каждый пик в интервале 2 π отображаемых полярных углов. Каждый пик соответствует точке, лежащей на окружности r = a . Сегменты линий, соединяющие последовательные вершины, образуют правильный многоугольник с четным числом вершин, центр которого находится в полюсе, а радиус - через каждую вершину, и аналогично:
- Розы симметричны относительно шеста.
- Розы симметричны относительно каждой линии, проходящей через полюс и вершину (через «середину» лепестка), при этом полярный угол между вершинами последовательных лепестков равен $⁠ 2 π / 2 k ⁠ = ⁠ π / k ⁠$ радиан. , эти розы обладают вращательной симметрией порядка $2k Таким образом$ .
- Розы симметричны относительно каждой линии, делящей пополам угол между последовательными вершинами, что соответствует границам полупериода и апофеме соответствующего многоугольника.

Когда k нечетно, роза состоит из k лепестков, по одному на каждый гребень (или впадину) в интервале 2 π отображаемых полярных углов. Каждый пик соответствует точке, лежащей на окружности r = a . Положительные и отрицательные полупериоды этой розы совпадают, а это означает, что при их построении графика необходимо отображать только положительные или только отрицательные полупериоды, чтобы сформировать полную кривую. (Эквивалентно, полная кривая будет построена путем построения любого непрерывного интервала полярных углов длиной π радиан, например от θ = 0 до θ = π . ^{[ 7 ]}) Отрезки линий, соединяющие последовательные вершины, образуют правильный многоугольник с нечетным числом вершин, а также:
- Розы симметричны относительно каждой линии, проходящей через полюс и вершину (через середину лепестка), при этом полярный угол между вершинами последовательных лепестков равен $⁠ 2 π / k ⁠$ радиан. Таким образом, эти розы обладают вращательной симметрией порядка $k$ .

Лепестки розы не перекрываются.

Розы могут быть заданы алгебраическими кривыми порядка $k + 1$ , когда $k$ нечетно, и $2(k + 1),$ когда $k$ четно. ^{[ 8 ]}

Круг

Роза с $k = 1$ — это круг , лежащий на полюсе, диаметр которого лежит на полярной оси, когда $r = a cos(θ)$ . Круг — это единственный лепесток кривой. (См. круг, образующийся в конце следующего раздела.) В декартовых координатах эквивалентные характеристики косинуса и синуса равны

\left(x-{\frac {a}{2}}\right)^{2}+y^{2}=\left({\frac {a}{2}}\right)^{2}

и

x^{2}+\left(y-{\frac {a}{2}}\right)^{2}=\left({\frac {a}{2}}\right)^{2}

соответственно.

Четырехлистный

Роза с $k = 2$ называется четырехлистной , потому что у нее $2k = 4$ лепестка. В декартовых координатах характеристики косинуса и синуса равны

\left(x^{2}+y^{2}\right)^{3}=a^{2}\left(x^{2}-y^{2}\right)^{2}

и

\left(x^{2}+y^{2}\right)^{3}=4\left(axy\right)^{2}

соответственно.

трехлистный

Роза с $k = 3$ называется трифолиумом. ^{[ 9 ]} потому что у него $k = 3$ лепестка. Кривую также называют Paquerette de Mélibée. В декартовых координатах характеристики косинуса и синуса равны

\left(x^{2}+y^{2}\right)^{2}=a\left(x^{3}-3xy^{2}\right)

и

\left(x^{2}+y^{2}\right)^{2}=-a\left(x^{3}-3xy^{2}\right)

соответственно. ^{[ 10 ]} (См. формирование трехлистника в конце следующего раздела.)

Октафолиум

Роза с $k = 4$ называется октафолиумом, потому что у нее $2k = 8$ лепестков. В декартовых координатах характеристики косинуса и синуса равны

\left(x^{2}+y^{2}\right)^{5}=a^{2}\left(x^{4}-6x^{2}y^{2}+y^{4}\right)^{2}

и

\left(x^{2}+y^{2}\right)^{5}=16a^{2}\left(xy^{3}-yx^{3}\right)^{2}

соответственно.

Пентафолий

Роза с $k = 5$ называется пентафолиумом , потому что у нее $k = 5$ лепестков. В декартовых координатах характеристики косинуса и синуса равны

\left(x^{2}+y^{2}\right)^{3}=a\left(x^{5}-10x^{3}y^{2}+5xy^{4}\right)

и

\left(x^{2}+y^{2}\right)^{3}=a\left(5x^{4}y-10x^{2}y^{3}+y^{5}\right)

соответственно.

Общая и лепестковая площади

Общая площадь розы с полярным уравнением вида $r = a cos(kθ)$ или $r = a sin(kθ)$ , где $k$ — целое число, отличное от нуля, равна ^{[ 11 ]}

{\begin{aligned}{\frac {1}{2}}\int _{0}^{2\pi }(a\cos(k\theta ))^{2}\,d\theta &={\frac {a^{2}}{2}}\left(\pi +{\frac {\sin(4k\pi )}{4k}}\right)={\frac {\pi a^{2}}{2}}&&\quad {\text{for even }}k\\[8px]{\frac {1}{2}}\int _{0}^{\pi }(a\cos(k\theta ))^{2}\,d\theta &={\frac {a^{2}}{2}}\left({\frac {\pi }{2}}+{\frac {\sin(2k\pi )}{4k}}\right)={\frac {\pi a^{2}}{4}}&&\quad {\text{for odd }}k\end{aligned}}

Если $k$ четное, $2k лепестков$ ; а когда $k$ нечетно, имеется $k$ лепестков, поэтому площадь каждого лепестка равна $⁠ πa 2 / 4 k ⁠$ .

Розы с рациональными числовыми значениями для $k$

В общем, когда $k$ - рациональное число в неприводимой дроби форме $k = ⁠ n / d ⁠$ , где $n$ и $d$ — ненулевые целые числа, количество лепестков — знаменатель выражения $⁠ 1 / 2 ⁠ - ⁠ 1 / 2 k ⁠ = ⁠ п - d / 2 п ⁠$ . ^{[ 12 ]} Это означает, что количество лепестков равно $n,$ если и $n,$ и $d$ нечетны, и $2 n$ в противном случае. ^{[ 13 ]}

В случае, когда и $n,$ и $d$ нечетны, положительный и отрицательный полупериоды синусоиды совпадают. График этих роз завершается в любом непрерывном интервале полярных углов $длиной dπ$ . ^{[ 14 ]}

Когда n четное, а d нечетное или наоборот, роза будет полностью изображена в непрерывном интервале полярных углов длиной 2 dπ . ^{[ 15 ]} Более того, розы симметричны относительно полюса как для косинусных, так и для синусоидальных характеристик. ^{[ 16 ]}
- Кроме того, когда $n$ нечетно, а $d$ четно, розы, заданные полярными уравнениями косинуса и синуса с одинаковыми значениями $a$ и $k,$ совпадают. Для такой пары роз роза с заданием синусоидальной функции совпадает с гребнем розы с заданием косинуса at на полярной оси либо при $θ = ⁠ dπ / 2 ⁠$ или при $θ = ⁠ 3 dπ / 2 ⁠$ . (Это означает, что розы $r = a cos(kθ)$ и $r = a sin(kθ)$ с ненулевыми целыми значениями $k$ никогда не совпадают.)

Роза вписана в круг $r = a$ , соответствующий радиальной координате всех ее вершин.

Лист Дюрера

Роза с $k = ⁠ 1/2 ⁠ Альбрехта гравера$ называется фолиумом Дюрера, по имени немецкого художника и Дюрера . Розы, указанные $r = a cos(⁠ θ / 2 ⁠)$ и $r = грех (⁠ θ / 2 ⁠)$ совпадают, хотя $cos (⁠ θ / 2 ⁠) \neq грех (⁠ θ / 2 ⁠)$ . В декартовых координатах роза определяется как ^{[ 17 ]}

\left(x^{2}+y^{2}\right)\left(2\left(x^{2}+y^{2}\right)-a^{2}\right)^{2}=a^{4}x^{2}

Лист Дюрера также представляет собой трисектрису — кривую, которую можно использовать для разделения углов пополам.

Лимасон трисектрикс

Роза с $k = ⁠ 1/3, ⁠ —$ это трисектриса Лимасона , обладающая свойством кривых трисектрисы которые можно использовать для разделения углов пополам. У розы один лепесток с двумя петлями. (Смотрите анимацию ниже.)

Примеры роз

r = cos(kθ),

созданных с использованием шестерен с разными передаточными числами.
Отображаемые лучи представляют собой полярную ось, а

θ = ⁠ π / 2 ⁠

.
Построение графика начинается с

θ = 2 π,

когда

k

является целым числом,

в противном случае θ = 2 dπ

, и продолжается по часовой стрелке до

θ = 0

.

Круг ( ,

k 1

знак равно

n знак равно 1

,

d знак равно 1

). Роза завершена, когда

θ = π (пол-оборота более легкой шестерни).

достигается

Лимасона Трисектриса ,

k = ⁠ 1/3 = ⁠ .

(

n = 1

,

d 3

), имеет один лепесток с двумя петлями Роза завершена, когда

θ = 3 π (

достигается ⁠ 3/2 оборота . более легкой передачи)

Трилистник,

k = 3

(

n = 3

,

d = 1

). Роза завершена, когда

θ = π (пол-оборота более легкой шестерни).

достигается

8 лепестков розы с

k = ⁠ 4 / 5 ⁠

(

n = 4

,

d = 5

) — это каждая отдельная петля, пересекающая другие лепестки. Роза симметрична относительно шеста. Роза завершена при

θ = 10 π

(пять оборотов более легкой шестерни).

Розы с иррациональными числовыми значениями для $k$

Розовая кривая, заданная иррациональным числом для $k,$ имеет бесконечное количество лепестков. ^{[ 18 ]} и никогда не завершится. Например, синусоида $r = a cos(πθ)$ имеет период $T = 2$ , поэтому у нее есть лепесток в интервале полярных углов $— ⁠ 1 / 2 ⁠ \leq θ \leq ⁠ 1/2 ⁠; с$ гребнем на полярной оси однако в области полярного уравнения нет другого полярного угла, который будет отображаться в координатах $(a,0)$ . В целом розы, заданные синусоидами с угловыми частотами, которые являются иррациональными константами, образуют плотное множество (то есть они сколь угодно близко подходят к заданию каждой точки в круге $r \leq a$ ).

См. также

Limaçon trisectrix — имеет ту же форму, что и роза с $k = ⁠ 1 / 3 ⁠$ .
Quadrifolium – роза, где $k = 2$ .
Маврская роза
Роза (топология)
Сектрикс Маклорена
Спирограф

Примечания

^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Родонея» , Архив истории математики MacTutor , Университет Сент-Эндрюс
^ Математические модели Х. Мартина Канди и А. П. Роллетта, второе издание, 1961 (Oxford University Press), стр. 73.
^ «Роза (Математика)» . Проверено 2 февраля 2021 г.
^ Роберт Ферреол. «Роза» . Проверено 3 февраля 2021 г.
^ Кса Ли. «Кривая розы» . Проверено 12 февраля 2021 г.
^ Эрик В. Вайсштейн. «Роза (Математика)» . Вольфрам Математический мир . Проверено 5 февраля 2021 г.
^ «Количество лепестков кривой родонеи нечетного индекса» . ProofWiki.org . Проверено 3 февраля 2021 г.
^ Роберт Ферреол. «Роза» . Проверено 3 февраля 2021 г.
^ «Трифолиум» . Проверено 2 февраля 2021 г.
^ Эрик В. Вайсштейн. «Пакерет де Мелибе» . Вольфрам Математический мир . Проверено 5 февраля 2021 г.
^ Роберт Ферреол. «Роза» . Проверено 3 февраля 2021 г.
^ Ян Вассенаар. «Родонея» . Проверено 2 февраля 2021 г.
^ Роберт Ферреол. «Роза» . Проверено 5 февраля 2021 г.
^ Кса Ли. «Кривая розы» . Проверено 12 февраля 2021 г.
^ Кса Ли. «Кривая розы» . Проверено 12 февраля 2021 г.
^ Ян Вассенаар. «Родонея» . Проверено 2 февраля 2021 г.
^ Роберт Ферреол. «Дюрер Фолиум» . Проверено 3 февраля 2021 г.
^ Эрик В. Вайсштейн. «Роза (Математика)» . Вольфрам Математический мир . Проверено 5 февраля 2021 г.

Внешние ссылки

Апплет для создания розы с $k$ параметром
Визуальный словарь специальных плоских кривых Кса Ли
Интерактивный пример с JSXGraph
Создайте розовую кривую в виде векторной графики (используя функцию синуса).

[1] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Родонея» , Архив истории математики MacTutor , Университет Сент-Эндрюс

[2] Математические модели Х. Мартина Канди и А. П. Роллетта, второе издание, 1961 (Oxford University Press), стр. 73.

[3] «Роза (Математика)» . Проверено 2 февраля 2021 г.

[4] Роберт Ферреол. «Роза» . Проверено 3 февраля 2021 г.

[5] Кса Ли. «Кривая розы» . Проверено 12 февраля 2021 г.

[6] Эрик В. Вайсштейн. «Роза (Математика)» . Вольфрам Математический мир . Проверено 5 февраля 2021 г.

[7] «Количество лепестков кривой родонеи нечетного индекса» . ProofWiki.org . Проверено 3 февраля 2021 г.

[8] Роберт Ферреол. «Роза» . Проверено 3 февраля 2021 г.

[9] «Трифолиум» . Проверено 2 февраля 2021 г.

[10] Эрик В. Вайсштейн. «Пакерет де Мелибе» . Вольфрам Математический мир . Проверено 5 февраля 2021 г.

[11] Роберт Ферреол. «Роза» . Проверено 3 февраля 2021 г.

[12] Ян Вассенаар. «Родонея» . Проверено 2 февраля 2021 г.

[13] Роберт Ферреол. «Роза» . Проверено 5 февраля 2021 г.

[14] Кса Ли. «Кривая розы» . Проверено 12 февраля 2021 г.

[15] Кса Ли. «Кривая розы» . Проверено 12 февраля 2021 г.

[16] Ян Вассенаар. «Родонея» . Проверено 2 февраля 2021 г.

[17] Роберт Ферреол. «Дюрер Фолиум» . Проверено 3 февраля 2021 г.

[18] Эрик В. Вайсштейн. «Роза (Математика)» . Вольфрам Математический мир . Проверено 5 февраля 2021 г.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

Общий обзор

Спецификация

Общие свойства

Лепестки

Симметрия

Розы с ненулевыми целочисленными значениями k

Круг

Четырехлистный

трехлистный

Октафолиум

Пентафолий

Общая и лепестковая площади

Розы с рациональными числовыми значениями для k

Лист Дюрера

Лимасон трисектрикс

Розы с иррациональными числовыми значениями для k

См. также

Примечания

Внешние ссылки

Розы с ненулевыми целочисленными значениями $k$

Розы с рациональными числовыми значениями для $k$

Розы с иррациональными числовыми значениями для $k$