Хакенбуш

Хакенбуш — игра для двух игроков, изобретенная математиком Джоном Хортоном Конвеем . ^[1] В нее можно играть на любой конфигурации цветных сегментов линий, соединенных друг с другом своими конечными точками и с «земной» линией.

Геймплей

Игра начинается с того, что игроки рисуют «земную» линию (обычно, но не обязательно, горизонтальную линию внизу листа или другой игровой площадки) и несколько сегментов линии так, чтобы каждый сегмент линии был соединен с землей либо напрямую, либо напрямую. в конечной точке или косвенно, через цепочку других сегментов, соединенных конечными точками. В одной точке может встречаться любое количество сегментов, поэтому может быть несколько путей к земле.

В свой ход игрок «обрезает» (стирает) любой отрезок линии по своему выбору. Каждый сегмент линии, больше не связанный с землей каким-либо путем, «падает» (т.е. стирается). Согласно общепринятому соглашению комбинаторной теории игр, первый игрок, который не может двигаться, проигрывает.

Доска Хакенбуша может состоять из конечного числа (в случае «конечной доски») или бесконечного числа (в случае «бесконечной доски») отрезков прямой. Существование бесконечного числа отрезков не нарушает предположения теории игр о том, что игру можно завершить за конечное время при условии, что существует только конечное число отрезков, непосредственно «касающихся» земли. На бесконечной доске, в зависимости от ее расположения, игра может продолжаться вечно, при условии, что земли касается бесконечно много точек.

Варианты

В оригинальной фольклорной версии «Хакенбуша» любому игроку разрешено срезать любое преимущество: поскольку это беспристрастная игра , сравнительно просто провести полный анализ с помощью теоремы Спрага – Гранди . Таким образом, версии Хакенбуша, представляющие интерес для комбинаторной теории игр, представляют собой более сложные партизанские игры , а это означает, что варианты (ходы), доступные одному игроку, не обязательно будут теми, которые доступны другому игроку, если бы настала его очередь делать ход, учитывая ту же позицию. . Это достигается одним из двух способов:

Оригинальный Хакенбуш: все сегменты линий одного цвета и могут быть разрезаны любым игроком. Это означает, что выигрыши симметричны, и каждый игрок выполняет одни и те же операции в зависимости от положения на доске (в данном случае структуры розыгрыша). Его еще называют Зеленый Хакенбуш. ^[2]
Сине-красный Хакенбуш : каждый сегмент линии окрашен в красный или синий цвет. Одному игроку (обычно первому или левому игроку) разрешено разрезать только синие сегменты линий, в то время как другому игроку (обычно второму или правому игроку) разрешено разрезать только красные сегменты линий.
Сине-красно-зеленый Хакенбуш : каждый сегмент линии окрашен в красный, синий или зеленый цвет. Правила такие же, как и для Blue-Red Hackenbush, с дополнительным условием, что сегменты зеленой линии может разрезать любой игрок.

Сине-красный Хакенбуш — это всего лишь частный случай Сине-красно-зеленого Хакенбуша, но его стоит отметить отдельно, поскольку его анализ зачастую гораздо проще. Это потому, что Blue-Red Hackenbush — это так называемая холодная игра , а это, по сути, означает, что первый ход никогда не может быть преимуществом.

Анализ

Хакенбуш часто использовался в качестве примера игры для демонстрации определений и концепций комбинаторной теории игр , начиная с его использования в книгах «Числа и игры» и «Пути к победе в математических играх» некоторых основателей этой области. В частности, Blue-Red Hackenbush можно использовать для построения сюрреалистических чисел : конечные сине-красные доски Hackenbush могут строить диадические рациональные числа , в то время как значения бесконечных Blue-Red Hackenbush учитывают действительные числа , порядковые номера и многие другие общие значения, которые ни один. Blue-Red-Green Hackenbush позволяет создавать дополнительные игры, значения которых не являются реальными числами, например, звезды и все другие числа .

Дальнейший анализ игры можно провести с помощью теории графов , рассматривая доску как набор вершин и ребер и исследуя пути к каждой вершине, лежащей на земле (которую следует рассматривать как выделенную вершину — идентифицировать не помешает). все точки земли вместе, а не в виде линии на графике).

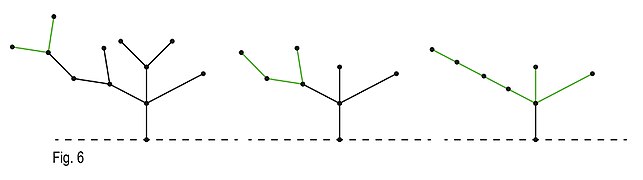
В беспристрастной версии Hackenbush (без цветов, заданных игроком) можно использовать кучи нимов, разбив игру на несколько случаев: вертикальные, сходящиеся и расходящиеся. В игре исключительно с вертикальными стопками отрезков линий, также называемых бамбуковыми стеблями, игра напрямую становится Нимом и может быть непосредственно проанализирована как таковая. Расходящиеся сегменты, или деревья, добавляют в игру дополнительную изюминку и требуют использования принципа двоеточия, гласящего, что, когда ветви сходятся в вершине, можно заменить ветви неветвящимся стеблем длины, равной их ним-сумме . Этот принцип меняет представление игры на более простую версию стеблей бамбука. Последний возможный набор графов, который можно построить, — это сходящиеся, также известные как графы с произвольным корнем. Используя принцип слияния, мы можем утверждать, что все вершины любого цикла могут быть объединены без изменения значения графа. ^[3] Следовательно, любой сходящийся граф можно интерпретировать как простой граф стебля бамбука. Объединив все три типа графиков, мы можем усложнить игру, даже не меняя Ним-сумму игры, тем самым позволяя игре использовать стратегии Нима.

Доказательство принципа двоеточия

Принцип двоеточия гласит, что, когда ветви сходятся в вершине, можно заменить ветви неветвящимся стеблем длиной, равной их нимсумме. но произвольный граф G и выберите произвольную вершину x в G. Рассмотрим фиксированный , Пусть H ₁ и H ₂ — произвольные деревья (или графы), имеющие одинаковое значение Шпрага-Грунди. Рассмотрим два графа G ₁ = G _x : H ₁ и G ₂ = G _x : H ₂ , где G _x : H _i представляет граф, построенный путем присоединения дерева H _i к вершине x графа G . Принцип двоеточия гласит, что два графика G1 и G2 имеют одинаковое значение Спрага-Грунди. Рассмотрим сумму двух игр. Утверждение о том, что G ₁ и G ₂ имеют одинаковое значение Шпрага-Грунди, эквивалентно утверждению, что сумма двух игр имеет значение Шпрага-Грунди 0. Другими словами, мы должны показать, что сумма G ₁ + G ₂ является P-позицией. Игроку гарантирована победа, если он станет вторым игроком, сделавшим ход в G ₁ + G ₂ . Если в одной из игр первый игрок делает ход, срезав одно из ребер в G , то второй игрок срезает то же ребро в одной из игр. G в другой игре. (Такая пара ходов может исключить H ₁ и H ₂ из игры, но в противном случае H ₁ и H ₂ не будут нарушены.) Если первый игрок делает ход, срезав ребро в H ₁ или H ₂ , то игра Спрэга-Гранди значения H ₁ и H ₂ больше не равны, так что существует ход в H ₁ или H ₂ , который сохраняет значения Спрэга-Грунди одинаковыми. Таким образом, вы всегда будете иметь ответ на каждое его движение. Это означает, что вы сделаете последний ход и выиграете. ^[4]

Пример, в котором игру можно сократить с помощью принципа двоеточия.

Ссылки

^ Дэвис, Том. «Что такое Хакенбуш?» . geometer.org . Проверено 12 февраля 2023 г.
^ https://webpages.charlotte.edu/~hbreiter/SVSM/amyspaper.pdf
^ Р., Берлекамп, Элвин (2001–2004 гг.). Выигрышные пути для ваших математических игр . Конвей, Джон Х. (Джон Хортон), Гай, Ричард К. (2-е изд.). Натик, Массачусетс: АК Питерс. ISBN 9781568811420 . OCLC 45102937 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Фергюсон, Томас С. (осень 2000 г.). «Теория игр» (PDF) .

Джон Х. Конвей, О числах и играх , 2-е издание, AK Peters, 2000.

Внешние ссылки

[1] Дэвис, Том. «Что такое Хакенбуш?» . geometer.org . Проверено 12 февраля 2023 г.

[2] ttps://webpages.charlotte.edu/~hbreiter/SVSM/amyspaper.pdf

[3] Р., Берлекамп, Элвин (2001–2004 гг.). Выигрышные пути для ваших математических игр . Конвей, Джон Х. (Джон Хортон), Гай, Ричард К. (2-е изд.). Натик, Массачусетс: АК Питерс. ISBN 9781568811420 . OCLC 45102937 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[4] Фергюсон, Томас С. (осень 2000 г.). «Теория игр» (PDF) .

[1]

[2]

[3]

[4]