Метод наискорейшего спуска

Алгоритм оптимизации см. в разделе Градиентный спуск .

В математике метод наискорейшего спуска или метод перевала является расширением метода Лапласа для аппроксимации интеграла, при котором контурный интеграл деформируется в комплексной плоскости так, чтобы он проходил вблизи стационарной точки ( седловой точки ), примерно в направлении крутой спуск или стационарная фаза. Приближение перевала используется с интегралами на комплексной плоскости, тогда как метод Лапласа используется с действительными интегралами.

Интеграл, который необходимо оценить, часто имеет вид

$\int _{C}f(z)e^{\lambda g(z)}\,dz,$

где C — контур, а λ велико. Одна из версий метода наискорейшего спуска деформирует контур интегрирования C в новый путь интегрирования C' так, что выполняются следующие условия:

1. C′ проходит через один или несколько нулей производной g ′( z ),
2. мнимая часть g ( z ) постоянна на C' .

Метод наискорейшего спуска был впервые опубликован Дебаем (1909) , который использовал его для оценки функций Бесселя и указал, что он встречается в неопубликованной заметке Римана (1863) о гипергеометрических функциях . Контур наискорейшего спуска обладает минимаксным свойством, см. Федорюк (2001) . Сигель (1932) описал некоторые другие неопубликованные заметки Римана, где он использовал этот метод для вывода формулы Римана-Зигеля .

Основная идея

Метод наискорейшего спуска — это метод аппроксимации комплексного интеграла вида $$I(\lambda )=\int _{C}f(z)e^{\lambda g(z)}\,\mathrm {d} z$$для больших $\lambda \rightarrow \infty$, где $f(z)$ и $g(z)$ являются аналитическими функциями $z$. Поскольку подынтегральная функция аналитична, контур $C$ можно деформировать в новый контур $C'$ без изменения интеграла. В частности, ищут новый контур, на котором мнимая часть, обозначаемая $\Im (\cdot )$, из $g(z)=\Re [g(z)]+i\,\Im [g(z)]$ постоянно ( $\Re (\cdot )$ обозначает действительную часть). Затем $$I(\lambda )=e^{i\lambda \Im \{g(z)\}}\int _{C'}f(z)e^{\lambda \Re \{g(z)\}}\,\mathrm {d} z,$$а оставшийся интеграл можно аппроксимировать другими методами, например методом Лапласа .

Этимология

Метод называется методом наискорейшего спуска, поскольку для аналитических $g(z)$, контуры постоянной фазы эквивалентны контурам наискорейшего спуска.

Если $g(z)=X(z)+iY(z)$ является аналитической функцией $z=x+iy$, он удовлетворяет уравнениям Коши–Римана $${\frac {\partial X}{\partial x}}={\frac {\partial Y}{\partial y}}\qquad {\text{and}}\qquad {\frac {\partial X}{\partial y}}=-{\frac {\partial Y}{\partial x}}.$$Затем $${\frac {\partial X}{\partial x}}{\frac {\partial Y}{\partial x}}+{\frac {\partial X}{\partial y}}{\frac {\partial Y}{\partial y}}=\nabla X\cdot \nabla Y=0,$$поэтому контуры постоянной фазы являются также контурами наискорейшего спуска.

Простая оценка

Пусть   f , S : C ^н → C и C ⊂ C ^н . Если

$M=\sup _{x\in C}\Re (S(x))<\infty ,$

где $\Re (\cdot )$ обозначает действительную часть, и существует положительное действительное число λ ₀ такое, что

$\int _{C}\left|f(x)e^{\lambda _{0}S(x)}\right|dx<\infty ,$

то имеет место следующая оценка:

$\left|\int _{C}f(x)e^{\lambda S(x)}dx\right|\leqslant {\text{const}}\cdot e^{\lambda M},\qquad \forall \lambda \in \mathbb {R} ,\quad \lambda \geqslant \lambda _{0}.$

Доказательство простой оценки:

${\begin{aligned}\left|\int _{C}f(x)e^{\lambda S(x)}dx\right|&\leqslant \int _{C}|f(x)|\left|e^{\lambda S(x)}\right|dx\\&\equiv \int _{C}|f(x)|e^{\lambda M}\left|e^{\lambda _{0}(S(x)-M)}e^{(\lambda -\lambda _{0})(S(x)-M)}\right|dx\\&\leqslant \int _{C}|f(x)|e^{\lambda M}\left|e^{\lambda _{0}(S(x)-M)}\right|dx&&\left|e^{(\lambda -\lambda _{0})(S(x)-M)}\right|\leqslant 1\\&=\underbrace {e^{-\lambda _{0}M}\int _{C}\left|f(x)e^{\lambda _{0}S(x)}\right|dx} _{\text{const}}\cdot e^{\lambda M}.\end{aligned}}$

Случай одной невырожденной седловой точки

Основные понятия и обозначения

Пусть x — комплексный n -мерный вектор и

$S''_{xx}(x)\equiv \left({\frac {\partial ^{2}S(x)}{\partial x_{i}\partial x_{j}}}\right),\qquad 1\leqslant i,\,j\leqslant n,$

обозначают матрицу Гессе для функции S ( x ) . Если

${\boldsymbol {\varphi }}(x)=(\varphi _{1}(x),\varphi _{2}(x),\ldots ,\varphi _{k}(x))$

является векторной функцией, то ее матрица Якоби определяется как

${\boldsymbol {\varphi }}_{x}'(x)\equiv \left({\frac {\partial \varphi _{i}(x)}{\partial x_{j}}}\right),\qquad 1\leqslant i\leqslant k,\quad 1\leqslant j\leqslant n.$

Невырожденная седловая точка , z ⁰ ∈ С ^н , голоморфной функции S ( z ) является критической точкой функции (т. е. ∇ S ( z ⁰ ) = 0 ), где матрица Гессе функции имеет ненулевой определитель (т. е. $\det S''_{zz}(z^{0})\neq 0$).

Основным инструментом построения асимптотики интегралов в случае невырожденной седловой точки является следующий:

Комплексная лемма Морса

Лемма Морса для вещественнозначных функций обобщается следующим образом. для голоморфных функций : вблизи невырожденной седловой точки z ⁰ голоморфной функции S ( z ) существуют координаты, в терминах которых S ( z ) − S ( z ⁰ ) точно квадратичен. Для уточнения пусть S — голоморфная функция с областью определения W ⊂ C ^н , и пусть z ⁰ в W — невырожденное седло S , т. е. ∇ S ( z ⁰ ) = 0 и $\det S''_{zz}(z^{0})\neq 0$. Тогда существуют окрестности U ⊂ W точки z ⁰ и V ⊂ C ^н w φ = 0 и биективная голоморфная функция φ : V → U с = (0) z ⁰ такой, что

$\forall w\in V:\qquad S({\boldsymbol {\varphi }}(w))=S(z^{0})+{\frac {1}{2}}\sum _{j=1}^{n}\mu _{j}w_{j}^{2},\quad \det {\boldsymbol {\varphi }}_{w}'(0)=1,$

Здесь µ _j — собственные значения матрицы $S_{zz}''(z^{0})$.

Иллюстрация комплексной леммы Морса.

Доказательство сложной леммы Морса.

Следующее доказательство является прямым обобщением доказательства вещественной леммы Морса , которое можно найти в. Начнем с демонстрации

Вспомогательное заявление. Пусть   f : C ^н → C голоморфен (0 ) в окрестности начала координат и   f = 0 . Тогда в некоторой окрестности существуют функции g _i : C ^н → C такой, что $$f(z)=\sum _{i=1}^{n}z_{i}g_{i}(z),$$ где g _i голоморфен и каждый $$g_{i}(0)=\left.{\tfrac {\partial f(z)}{\partial z_{i}}}\right|_{z=0}.$$

От личности

$f(z)=\int _{0}^{1}{\frac {d}{dt}}f\left(tz_{1},\cdots ,tz_{n}\right)dt=\sum _{i=1}^{n}z_{i}\int _{0}^{1}\left.{\frac {\partial f(z)}{\partial z_{i}}}\right|_{z=(tz_{1},\ldots ,tz_{n})}dt,$

мы заключаем, что

$g_{i}(z)=\int _{0}^{1}\left.{\frac {\partial f(z)}{\partial z_{i}}}\right|_{z=(tz_{1},\ldots ,tz_{n})}dt$

и

$g_{i}(0)=\left.{\frac {\partial f(z)}{\partial z_{i}}}\right|_{z=0}.$

Без ограничения общности переведем начало координат в z ⁰ , такой, что z ⁰ = 0 и S (0) = 0 . Используя вспомогательное утверждение, мы имеем

$S(z)=\sum _{i=1}^{n}z_{i}g_{i}(z).$

Поскольку начало координат является седловой точкой,

$\left.{\frac {\partial S(z)}{\partial z_{i}}}\right|_{z=0}=g_{i}(0)=0,$

мы также можем применить вспомогательное утверждение к функциям g _i ( z ) и получить

$S(z)=\sum _{i,j=1}^{n}z_{i}z_{j}h_{ij}(z).$ ( 1 )

Напомним, что произвольную матрицу A можно представить в виде суммы симметричных A ^{( с )} и антисимметричный A ^{( а )} матрицы,

$A_{ij}=A_{ij}^{(s)}+A_{ij}^{(a)},\qquad A_{ij}^{(s)}={\tfrac {1}{2}}\left(A_{ij}+A_{ji}\right),\qquad A_{ij}^{(a)}={\tfrac {1}{2}}\left(A_{ij}-A_{ji}\right).$

Сжатие любой симметричной матрицы B с произвольной матрицей A равно

$\sum _{i,j}B_{ij}A_{ij}=\sum _{i,j}B_{ij}A_{ij}^{(s)},$ ( 2 )

т. е. антисимметричный компонент A не дает вклада, потому что

$\sum _{i,j}B_{ij}C_{ij}=\sum _{i,j}B_{ji}C_{ji}=-\sum _{i,j}B_{ij}C_{ij}=0.$

Таким образом, h _ij ( z ) в уравнении (1) можно считать симметричным относительно перестановки индексов i и j . Обратите внимание, что

$\left.{\frac {\partial ^{2}S(z)}{\partial z_{i}\partial z_{j}}}\right|_{z=0}=2h_{ij}(0);$

следовательно, det( h _ij (0)) ≠ 0, поскольку начало координат является невырожденной седловой точкой.

Покажем по индукции , что существуют локальные координаты ) , z ₌ ψ ( _{u = ( u 1 , ... un} u ) , 0 = ψ ( 0 ) такие, что

$S({\boldsymbol {\psi }}(u))=\sum _{i=1}^{n}u_{i}^{2}.$ ( 3 )

Во-первых, предположим, что существуют локальные координаты y = ( y ₁ , ... y _n ), z = φ ( y ), 0 = φ (0) , такие, что

$S({\boldsymbol {\phi }}(y))=y_{1}^{2}+\cdots +y_{r-1}^{2}+\sum _{i,j=r}^{n}y_{i}y_{j}H_{ij}(y),$ ( 4 )

где H _ij симметричен согласно уравнению (2). Линейной заменой переменных ( y _r , ... y _n ) мы можем гарантировать, что H _rr (0) ≠ 0 . Из правила цепочки имеем

${\frac {\partial ^{2}S({\boldsymbol {\phi }}(y))}{\partial y_{i}\partial y_{j}}}=\sum _{l,k=1}^{n}\left.{\frac {\partial ^{2}S(z)}{\partial z_{k}\partial z_{l}}}\right|_{z={\boldsymbol {\phi }}(y)}{\frac {\partial \phi _{k}}{\partial y_{i}}}{\frac {\partial \phi _{l}}{\partial y_{j}}}+\sum _{k=1}^{n}\left.{\frac {\partial S(z)}{\partial z_{k}}}\right|_{z={\boldsymbol {\phi }}(y)}{\frac {\partial ^{2}\phi _{k}}{\partial y_{i}\partial y_{j}}}$

Поэтому:

$S''_{yy}({\boldsymbol {\phi }}(0))={\boldsymbol {\phi }}'_{y}(0)^{T}S''_{zz}(0){\boldsymbol {\phi }}'_{y}(0),\qquad \det {\boldsymbol {\phi }}'_{y}(0)\neq 0;$

откуда,

$0\neq \det S''_{yy}({\boldsymbol {\phi }}(0))=2^{r-1}\det \left(2H_{ij}(0)\right).$

Матрицу ( H _ij (0)) можно привести к жордановой нормальной форме : ( H _ij (0)) = LJL ⁻¹ , где L желаемое неособое линейное преобразование, а диагональ J содержит ненулевые собственные значения ( дает H _ij (0)) . Если H _ij (0) ≠ 0 , то в силу непрерывности H _ij ( y ) он также должен быть ненулевым в некоторой окрестности начала координат. представив ${\tilde {H}}_{ij}(y)=H_{ij}(y)/H_{rr}(y)$, мы пишем

${\begin{aligned}S({\boldsymbol {\varphi }}(y))=&y_{1}^{2}+\cdots +y_{r-1}^{2}+H_{rr}(y)\sum _{i,j=r}^{n}y_{i}y_{j}{\tilde {H}}_{ij}(y)\\=&y_{1}^{2}+\cdots +y_{r-1}^{2}+H_{rr}(y)\left[y_{r}^{2}+2y_{r}\sum _{j=r+1}^{n}y_{j}{\tilde {H}}_{rj}(y)+\sum _{i,j=r+1}^{n}y_{i}y_{j}{\tilde {H}}_{ij}(y)\right]\\=&y_{1}^{2}+\cdots +y_{r-1}^{2}+H_{rr}(y)\left[\left(y_{r}+\sum _{j=r+1}^{n}y_{j}{\tilde {H}}_{rj}(y)\right)^{2}-\left(\sum _{j=r+1}^{n}y_{j}{\tilde {H}}_{rj}(y)\right)^{2}\right]+H_{rr}(y)\sum _{i,j=r+1}^{n}y_{i}y_{j}{\tilde {H}}_{ij}(y)\end{aligned}}$

Руководствуясь последним выражением, введем новые координаты z = η ( x ), 0 = η (0),

$x_{r}={\sqrt {H_{rr}(y)}}\left(y_{r}+\sum _{j=r+1}^{n}y_{j}{\tilde {H}}_{rj}(y)\right),\qquad x_{j}=y_{j},\quad \forall j\neq r.$

Замена переменных y ↔ x локально обратима, поскольку соответствующий якобиан отличен от нуля,

$\left.{\frac {\partial x_{r}}{\partial y_{k}}}\right|_{y=0}={\sqrt {H_{rr}(0)}}\left[\delta _{r,\,k}+\sum _{j=r+1}^{n}\delta _{j,\,k}{\tilde {H}}_{jr}(0)\right].$

Поэтому,

$S({\boldsymbol {\eta }}(x))={x}_{1}^{2}+\cdots +{x}_{r}^{2}+\sum _{i,j=r+1}^{n}{x}_{i}{x}_{j}W_{ij}(x).$ ( 5 )

Сравнивая уравнения (4) и (5), приходим к выводу, что уравнение (3) проверено. Обозначая собственные значения $S''_{zz}(0)$ на µ _j уравнение (3) можно переписать как

$S({\boldsymbol {\varphi }}(w))={\frac {1}{2}}\sum _{j=1}^{n}\mu _{j}w_{j}^{2}.$ ( 6 )

Поэтому,

$S''_{ww}({\boldsymbol {\varphi }}(0))={\boldsymbol {\varphi }}'_{w}(0)^{T}S''_{zz}(0){\boldsymbol {\varphi }}'_{w}(0),$ ( 7 )

Из уравнения (6) следует, что $\det S''_{ww}({\boldsymbol {\varphi }}(0))=\mu _{1}\cdots \mu _{n}$. Жорданова нормальная форма $S''_{zz}(0)$ читает $S''_{zz}(0)=PJ_{z}P^{-1}$, где J _z — верхняя диагональная матрица, содержащая собственные значения и det P ≠ 0 ; следовательно, $\det S''_{zz}(0)=\mu _{1}\cdots \mu _{n}$. Из уравнения (7) получаем

$\det S''_{ww}({\boldsymbol {\varphi }}(0))=\left[\det {\boldsymbol {\varphi }}'_{w}(0)\right]^{2}\det S''_{zz}(0)\Longrightarrow \det {\boldsymbol {\varphi }}'_{w}(0)=\pm 1.$

Если $\det {\boldsymbol {\varphi }}'_{w}(0)=-1$, то замена двух переменных гарантирует, что $\det {\boldsymbol {\varphi }}'_{w}(0)=+1$.

Асимптотическое разложение в случае одной невырожденной седловой точки

Предполагать

1.  f ( z ) и S ( z ) — голоморфные функции в открытом , ограниченном и односвязном множестве Ω _x ⊂ C ^н такой, что I _x = Ω _x ∩ R ^н подключен ​ ;
2. $\Re (S(z))$ имеет единственный максимум: $\max _{z\in I_{x}}\Re (S(z))=\Re (S(x^{0}))$ ровно для одной точки x ⁰ я € _Икс ;
3. х ⁰ является невырожденным седлом (т. е. ∇ S ( x ⁰ ) = 0 и $\det S''_{xx}(x^{0})\neq 0$).

Тогда имеет место следующая асимптотика

$I(\lambda )\equiv \int _{I_{x}}f(x)e^{\lambda S(x)}dx=\left({\frac {2\pi }{\lambda }}\right)^{\frac {n}{2}}e^{\lambda S(x^{0})}\left(f(x^{0})+O\left(\lambda ^{-1}\right)\right)\prod _{j=1}^{n}(-\mu _{j})^{-{\frac {1}{2}}},\qquad \lambda \to \infty ,$ ( 8 )

где μ _j — собственные значения гессиана $S''_{xx}(x^{0})$ и $(-\mu _{j})^{-{\frac {1}{2}}}$ определяются с аргументами

$\left|\arg {\sqrt {-\mu _{j}}}\right|<{\tfrac {\pi }{4}}.$ ( 9 )

Это утверждение является частным случаем более общих результатов, представленных Федорюком (1987).

Вывод уравнения (8)

Иллюстрация к выводу уравнения (8)

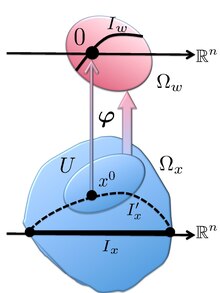
Сначала деформируем контур I _x в новый контур $I'_{x}\subset \Omega _{x}$ проходящий через седловую точку x ⁰ и делит границу с I _x . Эта деформация не меняет значения интеграла I ( λ ) . Мы используем Комплексную лемму Морса, чтобы изменить переменные интегрирования. Согласно лемме функция φ ( w ) отображает окрестность x ⁰ ∈ U ⊂ Ω _x на окрестность Ω _w, содержащую начало координат. Интеграл I ( λ ) можно разбить на два: I ( λ ) = I ₀ ( λ ) + I ₁ ( λ ) , где I ₀ ( λ ) — интеграл по $U\cap I'_{x}$, в то время как I ₁ ( λ ) закончилось $I'_{x}\setminus (U\cap I'_{x})$ (т.е. оставшаяся часть контура I′ _x ). Поскольку последняя область не содержит седловой точки x ⁰ , значение I ₁ ( λ ) экспоненциально меньше, чем I ₀ ( λ ) при λ → ∞ ; таким образом, I ₁ ( λ ) игнорируется. Введя контур I _w такой, что $U\cap I'_{x}={\boldsymbol {\varphi }}(I_{w})$, у нас есть

$I_{0}(\lambda )=e^{\lambda S(x^{0})}\int _{I_{w}}f[{\boldsymbol {\varphi }}(w)]\exp \left(\lambda \sum _{j=1}^{n}{\tfrac {\mu _{j}}{2}}w_{j}^{2}\right)\left|\det {\boldsymbol {\varphi }}_{w}'(w)\right|dw.$ ( 10 )

Вспоминая, что х ⁰ = φ (0), а также $\det {\boldsymbol {\varphi }}_{w}'(0)=1$, разложим предэкспоненциальную функцию $f[{\boldsymbol {\varphi }}(w)]$ в ряд Тейлора и оставить только главный член нулевого порядка

$I_{0}(\lambda )\approx f(x^{0})e^{\lambda S(x^{0})}\int _{\mathbf {R} ^{n}}\exp \left(\lambda \sum _{j=1}^{n}{\tfrac {\mu _{j}}{2}}w_{j}^{2}\right)dw=f(x^{0})e^{\lambda S(x^{0})}\prod _{j=1}^{n}\int _{-\infty }^{\infty }e^{{\frac {1}{2}}\lambda \mu _{j}y^{2}}dy.$ ( 11 )

Здесь мы заменили область интегрирования I _w на R ^н поскольку оба содержат начало координат, которое является седловой точкой, следовательно, они равны с точностью до экспоненциально малого члена. Интегралы в правой части уравнения (11) можно выразить как

${\mathcal {I}}_{j}=\int _{-\infty }^{\infty }e^{{\frac {1}{2}}\lambda \mu _{j}y^{2}}dy=2\int _{0}^{\infty }e^{-{\frac {1}{2}}\lambda \left({\sqrt {-\mu _{j}}}y\right)^{2}}dy=2\int _{0}^{\infty }e^{-{\frac {1}{2}}\lambda \left|{\sqrt {-\mu _{j}}}\right|^{2}y^{2}\exp \left(2i\arg {\sqrt {-\mu _{j}}}\right)}dy.$ ( 12 )

Из этого представления заключаем, что условие (9) должно выполняться, чтобы правая и левая части уравнения (12) совпадали. Согласно предположению 2, $\Re \left(S_{xx}''(x^{0})\right)$ является отрицательно определенной квадратичной формой (т. е., $\Re (\mu _{j})<0$), что означает существование интеграла ${\mathcal {I}}_{j}$, что легко вычисляется

${\mathcal {I}}_{j}={\frac {2}{{\sqrt {-\mu _{j}}}{\sqrt {\lambda }}}}\int _{0}^{\infty }e^{-{\frac {\xi ^{2}}{2}}}d\xi ={\sqrt {\frac {2\pi }{\lambda }}}(-\mu _{j})^{-{\frac {1}{2}}}.$

Уравнение (8) также можно записать как

$I(\lambda )=\left({\frac {2\pi }{\lambda }}\right)^{\frac {n}{2}}e^{\lambda S(x^{0})}\left(\det(-S_{xx}''(x^{0}))\right)^{-{\frac {1}{2}}}\left(f(x^{0})+O\left(\lambda ^{-1}\right)\right),$ ( 13 )

где филиал

${\sqrt {\det \left(-S_{xx}''(x^{0})\right)}}$

выбирается следующим образом

${\begin{aligned}\left(\det \left(-S_{xx}''(x^{0})\right)\right)^{-{\frac {1}{2}}}&=\exp \left(-i{\text{ Ind}}\left(-S_{xx}''(x^{0})\right)\right)\prod _{j=1}^{n}\left|\mu _{j}\right|^{-{\frac {1}{2}}},\\{\text{Ind}}\left(-S_{xx}''(x^{0})\right)&={\tfrac {1}{2}}\sum _{j=1}^{n}\arg(-\mu _{j}),&&|\arg(-\mu _{j})|<{\tfrac {\pi }{2}}.\end{aligned}}$

Рассмотрим важные частные случаи:

• Если S ( x ) имеет вещественное значение для реальных x и x ⁰ в Р ^н (он же многомерный метод Лапласа ), то $${\text{Ind}}\left(-S_{xx}''(x^{0})\right)=0.$$
• Если S ( x ) является чисто мнимым для вещественного x (т. е. $\Re (S(x))=0$ для всех x в R ^н ) и х ⁰ в Р ^н (он же многомерный метод стационарной фазы ), затем $${\text{Ind}}\left(-S_{xx}''(x^{0})\right)={\frac {\pi }{4}}{\text{sign }}S_{xx}''(x_{0}),$$ где ${\text{sign }}S_{xx}''(x_{0})$ обозначает сигнатуру матрицы $S_{xx}''(x_{0})$, что равно количеству отрицательных собственных значений минус количество положительных. Примечательно, что в приложениях метода стационарной фазы к многомерному приближению ВКБ в квантовой механике (а также в оптике) Ind связан с индексом Маслова, см., например, Чайчян и Демичев (2001) и Шульман (2005) .

Случай нескольких невырожденных седловых точек

Если функция S ( x ) имеет несколько изолированных невырожденных седловых точек, т. е.

$\nabla S\left(x^{(k)}\right)=0,\quad \det S''_{xx}\left(x^{(k)}\right)\neq 0,\quad x^{(k)}\in \Omega _{x}^{(k)},$

где

$\left\{\Omega _{x}^{(k)}\right\}_{k=1}^{K}$

является открытым покрытием Ω x _, то вычисление интегральной асимптотики сводится к случаю одной седловой точки с использованием разбиения единицы . Разбиение единицы позволяет построить набор непрерывных функций ρ _k ( x ) : Ω _x → [0, 1], 1 ⩽ k ⩽ K , таких, что

${\begin{aligned}\sum _{k=1}^{K}\rho _{k}(x)&=1,&&\forall x\in \Omega _{x},\\\rho _{k}(x)&=0&&\forall x\in \Omega _{x}\setminus \Omega _{x}^{(k)}.\end{aligned}}$

Откуда,

$\int _{I_{x}\subset \Omega _{x}}f(x)e^{\lambda S(x)}dx\equiv \sum _{k=1}^{K}\int _{I_{x}\subset \Omega _{x}}\rho _{k}(x)f(x)e^{\lambda S(x)}dx.$

Поэтому при λ → ∞ имеем:

$\sum _{k=1}^{K}\int _{{\text{a neighborhood of }}x^{(k)}}f(x)e^{\lambda S(x)}dx=\left({\frac {2\pi }{\lambda }}\right)^{\frac {n}{2}}\sum _{k=1}^{K}e^{\lambda S\left(x^{(k)}\right)}\left(\det \left(-S_{xx}''\left(x^{(k)}\right)\right)\right)^{-{\frac {1}{2}}}f\left(x^{(k)}\right),$

где на последнем этапе использовалось уравнение (13), а предэкспоненциальная функция   f ( x ) как минимум должна быть непрерывной.

Другие случаи

Когда ∇ S ( z ⁰ ) = 0 и $\det S''_{zz}(z^{0})=0$, точка z ⁰ ∈ С ^н называется вырожденной седловой точкой функции S ( z ) .

Вычисление асимптотики

$\int f(x)e^{\lambda S(x)}dx,$

когда λ → ∞, f ( x ) непрерывна, а S ( z ) имеет вырожденную седловую точку, представляет собой очень сложную задачу, решение которой в значительной степени опирается на теорию катастроф . Здесь теория катастроф заменяет лемму Морса , справедливую только в невырожденном случае, для преобразования функции S ( z ) в одно из множества канонических представлений. Более подробную информацию см., например, в Poston & Stewart (1978) и Fedoryuk (1987) .

Интегралы с вырожденными седловыми точками естественным образом появляются во многих приложениях, включая оптическую каустику и многомерное приближение ВКБ в квантовой механике.

Остальные случаи, например, когда   f ( x ) и/или S ( x ) являются разрывными или когда экстремум S ( x ) лежит на границе области интегрирования, требуют особого внимания (см., например, Федорюк (1987) и Вонг (1989) ).

Расширения и обобщения

Расширением метода наискорейшего спуска является так называемый нелинейный метод стационарной фазы/наискорейшего спуска . Здесь вместо интегралов нужно асимптотически оценивать решения задач факторизации Римана–Гильберта .

Учитывая контур C в комплексной сфере , функцию f, определенную на этом контуре, и специальную точку, скажем, бесконечность, ищут функцию M, голоморфную вдали от контура C , с заданным переходом через C и с заданной нормализацией на бесконечности. Если f и, следовательно, M являются матрицами, а не скалярами, то эта проблема, вообще говоря, не допускает явного решения.

Тогда возможна асимптотическая оценка в соответствии с методом линейной стационарной фазы/наискорейшего спуска. Идея состоит в том, чтобы асимптотически свести решение данной проблемы Римана–Гильберта к решению более простой, явно решаемой проблемы Римана–Гильберта. Теорема Коши используется для обоснования деформаций контура скачка.

Нелинейная стационарная фаза была введена Дейфтом и Чжоу в 1993 году на основе более ранней работы российского математика Александра Итса. (Собственно говоря) нелинейный метод наискорейшего спуска был представлен Камвиссисом, К. Маклафлином и П. Миллером в 2003 году на основе предыдущих работ Лакса, Левермора, Дейфта, Венакидеса и Чжоу. Как и в линейном случае, контуры наискорейшего спуска решают задачу мин-макс. В нелинейном случае они оказываются «S-образными кривыми» (определенными в другом контексте еще в 80-х годах Шталем, Гончаром и Рахмановым).

Нелинейный метод стационарной фазы/наискорейшего спуска имеет приложения в теории солитонных уравнений и интегрируемых моделях , случайных матрицах и комбинаторике .

Другое расширение - это метод Честера-Фридмана-Урселла для объединения седловых точек и равномерных асимптотических расширений.

См. также

• Интеграл Пирси
• Приближение стационарной фазы
• метод Лапласа

Ссылки

• Чайчян, М.; Демичев, А. (2001), Интегралы по траекториям в физике, том 1: случайный процесс и квантовая механика , Тейлор и Фрэнсис, с. 174, ISBN  075030801X
• Дебай, П. (1909), «Приближенные формулы для цилиндрических функций при больших значениях аргумента и бесконечно переменных значениях индекса» , Mathematical Annals , 67 (4): 535–558, doi : 10.1007/ BF01450097 , S2CID   122219667 перевод на английский язык Дебай, Питер Дж. В. (1954), Сборник статей Питера Дж. В. Дебая , Interscience Publishers, Inc., Нью-Йорк, ISBN  978-0-918024-58-9 , МР   0063975
• Дейфт, П.; Чжоу, X. (1993), «Метод наискорейшего спуска для колебательных задач Римана-Гильберта. Асимптотика уравнения МКдВ», Ann. математики. , том. 137, нет. 2, Анналы математики, Том. 137, № 2, стр. 295–368, arXiv : math/9201261 , doi : 10.2307/2946540 , JSTOR   2946540 , S2CID   12699956 .
• Эрдели А. (1956), Асимптотические разложения , Дувр .
• Федорюк, М.В. (2001) [1994], «Метод перевала» , Энциклопедия Математики , EMS Press .
• Федорюк М.В. (1987), Асимптотика: интегралы и ряды , Наука, Москва .
• Камвиссис, С.; Маклафлин, КТ-Р.; Миллер, П. (2003), «Полуклассические солитонные ансамбли для фокусирующего нелинейного уравнения Шредингера», Annals of Mathematics Studies , vol. 154, Издательство Принстонского университета .
• Риман, Б. (1863), О развитии частного двух гипергеометрических рядов в бесконечной цепной дроби (неопубликованная заметка, воспроизведена в сборнике статей Римана).
• Сигель, CL (1932), «О наследии Римана в аналитической теории чисел», Источники и исследования по истории математики, астрономии и физики , 2 : 45–80 , перепечатано в сборнике статей, том 1. Берлин: Springer-Verlag, 1966.
  • Переведено на Баркан, Эрик; Склар, Дэвид (2018), «О наласе Римана для аналитической теории чисел: перевод Убера Сигела», arXiv : 1810.05198 [ math.HO ] .
• Постон, Т.; Стюарт, И. (1978), Теория катастроф и ее приложения , Питман .
• Шульман, Л.С. (2005), «Глава 17: Фаза квазиклассической амплитуды», Методы и приложения интеграции путей , Дувр, ISBN  0486445283
• Вонг, Р. (1989), Асимптотические приближения интегралов , Academic Press .