Эпициклоида

В геометрии — эпициклоида (также называемая гиперциклоидой ). [1] — это плоская кривая, полученная путем отслеживания пути выбранной точки на окружности круга , называемого эпициклом , который катится, не скользя по фиксированному кругу. Это особый вид рулетки .
Эпициклоида с малым радиусом (R2), равным 0, представляет собой круг. Это вырожденная форма.
Уравнения
[ редактировать ]Если меньший круг имеет радиус , а больший круг имеет радиус , то параметрические уравнения кривой могут быть заданы следующим образом:
или:
Это можно записать в более краткой форме, используя комплексные числа: [2]
где
- угол
- меньший круг имеет радиус , и
- больший круг имеет радиус .
Площадь и длина дуги
[ редактировать ](Предполагая, что начальная точка лежит на большем круге.) Когда целое положительное число, площадь и длина дуги этой эпициклоиды
Это означает, что эпициклоида больше по площади, чем исходный неподвижный круг.
Если является целым положительным числом, то кривая замкнута и имеет k точек возврата (т. е. острых углов).
Если это рациональное число , скажем выражается в виде неприводимой дроби , то кривая имеет вид выступы.
| Чтобы замкнуть кривую и |
| выполнить 1-й повторяющийся узор: |
| θ = от 0 до q оборотов |
| α = от 0 до p вращений |
| общее количество оборотов внешнего катящегося круга = p + q оборотов |
Подсчитайте обороты анимации, чтобы увидеть p и q.
Если является иррациональным числом , то кривая никогда не замыкается и образует плотное подмножество пространства между большим кругом и кругом радиуса .
Расстояние от начала до точки на маленьком круге меняется вверх и вниз, как
где
- = радиус большого круга и
- = диаметр малого круга.
- Примеры эпициклоиды
- к = 1 ; кардиоида
- к = 2 ; нефроид
- к = 3 ; трилистник
- к = 4 ; четырехлистник
- к = 2,1 = 21/10
- к = 3,8 = 19/5
- к = 5,5 = 11/2
- к = 7,2 = 36/5
Эпициклоида — особый вид эпитрохоиды .
Эпицикл с одной створок — кардиоидный , с двумя створок — нефроид .
Эпициклоида и эволюта подобны ее . [3]
Доказательство
[ редактировать ]
Мы предполагаем, что позиция это то, что мы хотим решить, это угол между касательной точкой и движущейся точкой , и - это угол от начальной точки до точки касания.
Поскольку между двумя циклами нет скольжения, то мы имеем следующее:
По определению угла (который представляет собой дугу скорости по радиусу), мы имеем, что
и
- .
Из этих двух условий получаем тождество
- .
Вычислив, мы получим соотношение между и , что
- .
На рисунке мы видим положение точки на маленьком круге ясно.
См. также
[ редактировать ]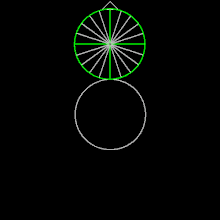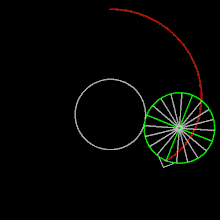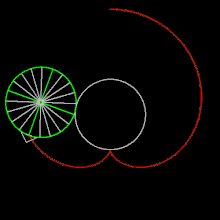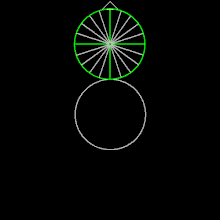
- Список периодических функций
- циклоида
- Циклогон
- Деферент и эпицикл
- Эпициклическая передача
- Эпитрохоид
- Гипоциклоида
- Гипотрохоид
- Набор Мультиброт
- Рулетка (кривая)
- Спирограф
Ссылки
[ редактировать ]- Дж. Деннис Лоуренс (1972). Каталог специальных плоских кривых . Дуврские публикации. стр. 161, 168–170, 175 . ISBN 978-0-486-60288-2 .
- ^ [1]
- ^ Эпициклоиды и продукты Бляшке Чунлея Цао, Аластера Флетчера, Чжуань Е.
- ^ Эпициклоидная эволюция - из Wolfram MathWorld
- ^ Пьетрокола, Джорджио (2005). «Тартапелаго» . Маэкла .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Эпициклоида» . Математический мир .
- « Эпициклоида » Майкла Форда, Демонстрационный проект Вольфрама , 2007 г.
- О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Эпициклоида» , Архив истории математики MacTutor , Университет Сент-Эндрюс
- Анимация эпициклоидов, перициклоидов и гипоциклоидов
- Спирограф -- GeoFun
- Историческая справка о применении эпициклоиды в форме зубьев шестерни.





![{\displaystyle \theta \in [0,2\pi],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/447f09acb3212adffba88ba2ef9af96f18ad6e85)






























