Гиперболатические функции

Графика, описывающая функцию гиперболастика типа I с различными значениями параметров.

Графика, описывающая функцию гиперболастика типа I с различными значениями параметров.

Графика, описывающая функцию Hyperbolastic Type II с различными значениями параметров.

Графика, описывающая функцию Hyperbolastic Type II с различными значениями параметров.

Графика, описывающая функцию Hyperbolastic Type III с различными значениями параметров.

Графика, описывающая гиперболистическую кумулятивную функцию распределения типа III с различными значениями параметров.

Графика, описывающая гиперболическую функцию плотности вероятности типа III с различными значениями параметров.

Гиперболатические функции , также известные как гиперболатические модели роста , представляют собой математические функции , которые используются в медицинском статистическом моделировании . Эти модели изначально были разработаны для отражения динамики роста многоклеточных опухолевых сфер и были представлены в 2005 году Мохаммадом Табатабаи, Дэвидом Уильямсом и Зораном Бурсаком. Точность гиперболастических функций при моделировании проблем реального мира в некоторой степени обусловлена ​​их гибкостью в точке перегиба. Эти функции можно использовать в самых разных задачах моделирования, таких как рост опухоли, пролиферация стволовых клеток , кинетика фармацевтических препаратов, рост рака, функция активации сигмовидной кишки в нейронных сетях , а также прогрессирование или регресс эпидемиологических заболеваний.

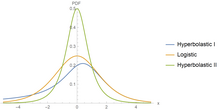
Гиперболатические функции могут моделировать кривые как роста, так и спада, пока не будет достигнута несущая способность . Благодаря своей гибкости, эти модели имеют разнообразные применения в области медицины, поскольку способны фиксировать прогрессирование заболевания с помощью промежуточных данных.уход. Как показывают рисунки, гиперболатические функции могут соответствовать сигмоидальной кривой, указывающей, что наименьшая скорость наблюдается при ранняя и поздняя стадии. Помимо сигмовидной формы, он также может использоваться в двухфазных ситуациях, когда медицинские вмешательства замедляют или обращают вспять прогрессирование заболевания; но когда эффект лечения исчезнет, ​​болезнь начнет вторая фаза его прогрессии до достижения горизонтальной асимптоты.

Одна из основных характеристик этих функций заключается в том, что они не только соответствуют сигмоидальным формам, но также могут моделировать двухфазные модели роста, которые другие классические сигмоидальные кривые не могут адекватно моделировать. Эта отличительная особенность имеет выгодное применение в различных областях, включая медицину, биологию, экономику, инженерию, агрономию и теорию автоматизированных систем.

Функция H1

Гиперболическое уравнение скорости типа I , обозначаемое H1, имеет вид

$${\frac {dP(x)}{dx}}={\frac {P(x)}{M}}\left(M-P\left(x\right)\right)\left(\delta +{\frac {\theta }{\sqrt {1+x^{2}}}}\right),$$

где $x$ любое действительное число и $P\left(x\right)$ численность населения в $x$. Параметр $M$ представляет грузоподъемность и параметры $\delta$ и $\theta$ совместно представляют темпы роста. Параметр $\theta$ дает расстояние от симметричной сигмоидальной кривой. Решение гиперболического уравнения скорости I типа для $P\left(x\right)$ дает

$$P(x)={\frac {M}{1+\alpha e^{-\delta x-\theta \operatorname {arsinh} (x)}}},$$

где $\operatorname {arsinh}$ – обратная гиперболическая функция синуса . Если кто-то желает использовать начальное условие $P\left(x_{0}\right)=P_{0}$, затем $\alpha$ может быть выражено как

$\alpha ={\frac {M-P_{0}}{P_{0}}}e^{\delta x_{0}+\theta \operatorname {arsinh} (x_{0})}$.

Если $x_{0}=0$, затем $\alpha$ сводится к

$\alpha ={\frac {M-P_{0}}{P_{0}}}$.

Если для лучшего соответствия модели необходим вертикальный сдвиг, можно добавить параметр сдвига. $\zeta$, что приведет к следующей формуле

$P(x)={\frac {M}{1+\alpha e^{-\delta x-\theta \operatorname {arsinh} (x)}}}+\zeta$.

Гиперболатическая функция типа I обобщает логистическую функцию . Если параметры $\theta =0$, то это станет логистической функцией. Эта функция $P(x)$ — гиперболатическая функция I типа . Стандартная гиперболатическая функция типа I равна

$P(x)={\frac {1}{1+e^{-x-\theta \operatorname {arsinh} (x)}}}$.

Функция H2

Гиперболическое уравнение скорости типа II , обозначаемое H2, определяется как

${\frac {dP(x)}{dx}}={\frac {\alpha \delta \gamma P^{2}(x)x^{\gamma -1}}{M}}\tanh \left({\frac {M-P(x)}{\alpha P(x)}}\right),$

где $\tanh$ - функция гиперболического тангенса , $M$ - это грузоподъемность, и оба $\delta$ и $\gamma >0$ совместно определить темпы роста. Кроме того, параметр $\gamma$ представляет собой ускорение хода времени. Решение гиперболатической функции скорости II типа для $P\left(x\right)$ дает

$P(x)={\frac {M}{1+\alpha \operatorname {arsinh} \left(e^{-\delta x^{\gamma }}\right)}}$.

Если кто-то желает использовать начальное условие $P(x_{0})=P_{0},$ затем $\alpha$ может быть выражено как

$\alpha ={\frac {M-P_{0}}{P_{0}\operatorname {arsinh} \left(e^{-\delta x_{0}^{\gamma }}\right)}}$.

Если $x_{0}=0$, затем $\alpha$ сводится к

$\alpha ={\frac {M-P_{0}}{P_{0}\operatorname {arsinh} (1)}}$.

Аналогично, если для лучшего соответствия необходим вертикальный сдвиг, можно использовать следующую формулу

$P(x)={\frac {M}{1+\alpha \operatorname {arsinh} \left(e^{-\delta x^{\gamma }}\right)}}+\zeta$.

Стандартная гиперболатическая функция типа II определяется как

$P(x)={\frac {1}{1+\operatorname {arsinh} \left(e^{-x}\right)}}$.

Функция H3

Гиперболатическое уравнение скорости типа III обозначается H3 и имеет вид

${\frac {dP(t)}{dt}}=\left(M-P\left(t\right)\right)\left(\delta \gamma t^{\gamma -1}+{\frac {\theta }{\sqrt {1+\theta ^{2}t^{2}}}}\right)$,

где $t$ > 0. Параметр $M$ представляет собой грузоподъемность, а параметры $\delta ,$ $\gamma ,$ и $\theta$ совместно определить темпы роста. Параметр $\gamma ,$ представляет собой ускорение шкалы времени, а размер $\theta$ представляет собой расстояние от симметричной сигмоидальной кривой. Решение дифференциального уравнения типа III имеет вид

$P(t)=M-\alpha e^{-\delta t^{\gamma }-\operatorname {arsinh} (\theta t)}$,

с начальным состоянием $P\left(t_{0}\right)=P_{0}$ мы можем выразить $\alpha$ как

$\alpha =\left(M-P_{0}\right)e^{\delta t_{0}^{\gamma }+\operatorname {arsinh} (\theta t_{0})}$.

Гиперболатическое распределение типа III представляет собой трехпараметрическое семейство непрерывных вероятностных распределений с масштабными параметрами $\delta$ > 0, и $\theta$ ≥ 0 и параметр $\gamma$ как параметр формы . Когда параметр $\theta$ = 0 гиперболатическое распределение типа III сводится к распределению Вейбулла . Гиперболатическая кумулятивная функция распределения типа III имеет вид

$F(x;\delta ,\gamma ,\theta )={\begin{cases}1-e^{-\delta x^{\gamma }-\operatorname {arsinh} (\theta x)}&x\geq 0,\\0&x<0\end{cases}}$,

и соответствующая ей функция плотности вероятности равна

$f(x;\delta ,\gamma ,\theta )={\begin{cases}e^{-\delta x^{\gamma }-\operatorname {arsinh} (\theta x)}\left(\delta \gamma x^{\gamma -1}+{\frac {\theta }{\sqrt {1+\theta ^{2}x^{2}}}}\right)&x\geq 0,\\0&x<0\end{cases}}$.

Функция опасности $h$ (или интенсивность отказов) определяется выражением

$h\left(x;\delta ,\gamma ,\theta \right)=\delta \gamma x^{\gamma -1}+{\frac {\theta }{\sqrt {1+x^{2}\theta ^{2}}}}.$

Функция выживания $S$ дается

$S(x;\delta ,\gamma ,\theta )=e^{-\delta x^{\gamma }-\operatorname {arsinh} (\theta x)}.$

Стандартная гиперболатическая кумулятивная функция распределения типа III определяется как

$F\left(x\right)=1-e^{-x-\operatorname {arsinh} (x)}$,

и соответствующая ей функция плотности вероятности равна

$f(x)=e^{-x-\operatorname {arsinh} (x)}\left(1+{\frac {1}{\sqrt {1+x^{2}}}}\right)$.

Характеристики

Если кто-то желает вычислить точку $x$ где популяция достигает процента от своей пропускной способности $M$, затем можно решить уравнение

$P(x)=kM$

для $x$, где $0<k<1$. Например, половину точки можно найти, установив $k={\frac {1}{2}}$.

Приложения

3D-гиперболатический график биомассы фитопланктона в зависимости от концентрации питательных веществ и времени

По словам исследователей стволовых клеток из Института регенеративной медицины Макгоуэна при Питтсбургском университете, «более новая модель [называемая гиперболастикой типа III или] H3 представляет собой дифференциальное уравнение , которое также описывает рост клеток. Эта модель допускает гораздо больше вариаций и имеет было доказано, что они лучше прогнозируют рост».

Модели гиперболатического роста H1, H2 и H3 применялись для анализа роста солидной карциномы Эрлиха с использованием различных методов лечения.

В зоотехнике гиперболатические функции были использованы для моделирования роста цыплят-бройлеров. Гиперболатическая модель III типа использовалась для определения размеров заживающей раны.

В области заживления ран гиперболатические модели точно отражают ход заживления. Такие функции использовались для исследования различий в скорости заживления различных типов ран и на разных стадиях процесса заживления с учетом содержания микроэлементов, факторов роста, диабетических ран и питания.

Другое применение гиперболастических функций находится в области стохастического диффузионного процесса. средняя функция которого является гиперболической кривой. Изучены основные характеристики процесса и рассмотрена максимально правдоподобная оценка параметров процесса. Для этого применяется метаэвристический алгоритм оптимизации Firefly после ограничения параметрического пространства поэтапной процедурой. Некоторые примеры, основанные на смоделированных путях отбора проб и реальных данных, иллюстрируют это развитие. Образец траектории процесса диффузии моделирует траекторию частицы, погруженной в текущую жидкость и подвергающейся случайным смещениям из-за столкновений с другими частицами, что называется броуновским движением . Гиперболатическая функция типа III была использована для моделирования пролиферации как взрослых мезенхимальных , так и эмбриональных стволовых клеток ; и гиперболатическая смешанная модель типа II использовалась при моделировании данных о раке шейки матки . Гиперболатические кривые могут быть важным инструментом при анализе клеточного роста, подборе биологических кривых, росте фитопланктона и мгновенной скорости зрелости.

В экологии и управлении лесами гиперболатические модели применялись для моделирования взаимосвязи между DBH и высотой.

многовариантная гиперболастическая модель III типа . Для анализа динамики роста фитопланктона с учетом концентрации питательных веществ использована

Гиперболатические регрессии

Кумулятивная функция распределения гиперболастического типа I, логистического и гиперболастического типа II

PDF-файл с отчетами H1, Логистика и H2

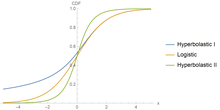
Гиперболастическая регрессия — это статистические модели , которые используют стандартные гиперболатические функции для моделирования дихотомической или полиномиальной конечной переменной. Цель гиперболатической регрессии — предсказать результат, используя набор объясняющих (независимых) переменных. Эти типы регрессий обычно используются во многих областях, включая медицину, общественное здравоохранение, стоматологию, биомедицину, а также социальные, поведенческие и инженерные науки. Например, бинарный регрессионный анализ использовался для прогнозирования эндоскопических поражений при железодефицитной анемии . применялась бинарная регрессия для дифференциации злокачественных и доброкачественных образований придатков . Кроме того, перед операцией

Бинарная гиперболатическая регрессия I типа

Позволять $Y$ быть двоичной переменной результата, которая может принимать одно из двух взаимоисключающих значений: успех или неудача. Если мы закодируем успех как $Y=1$ и неудача как $Y=0$, то для параметра $\theta \geq -1$, гиперболатическая вероятность успеха типа I с выборкой размером $n$ как функция параметра $\theta$ и вектор параметров ${\boldsymbol {\beta }}=(\beta _{0},\beta _{1},\ldots ,\beta _{p})$ учитывая $p$-мерный вектор объясняющих переменных определяется как $\mathbf {x} _{i}=(x_{i1},\ x_{i2},\ldots ,\ x_{ip})^{T}$, где $i=1,2,\ldots ,n$, определяется

$\pi (\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})-\theta \operatorname {arsinh} (\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}}}$.

Шансы на успех – это отношение вероятности успеха к вероятности неудачи. Для бинарной гиперболатической регрессии типа I шансы на успех обозначаются как $Odds_{H1}$ и выражается уравнением

$Odds_{H1}=e^{\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}}+\theta \operatorname {arsinh} (\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}$.

Логарифм $Odds_{H1}$ называется логитом бинарной гиперболатической регрессии типа I. Логит-преобразование обозначается через $L_{H1}$ и может быть записано как

$L_{H1}=\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}}+\theta \operatorname {arsinh} [\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}}]$.

Информация Шеннона для бинарной гиперболастики типа I (H1)

Информация Шеннона для случайной величины $Y$ определяется как

$I(y)=-{log}_{b}P(y)$

где основание логарифма $b>0$ и $b\neq 1$. Для двоичного результата $b$ равно $2$.

Для бинарной гиперболатической регрессии типа I информация $I(y)$ дается

$I(y)={\begin{cases}-log_{b}{\frac {1}{1+e^{-Z-\theta \operatorname {arsinh} (Z)}}}&y=1,\\-log_{b}{\frac {e^{-Z-\theta \operatorname {arsinh} (Z)}}{1+e^{-Z-\theta \operatorname {arsinh} (Z)}}}&y=0\end{cases}}$,

где $Z=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{s}$, и $x_{s}$ это $s^{th}$ входные данные.Для случайной выборки бинарных результатов размером $n$, среднюю эмпирическую информацию для гиперболатического H1 можно оценить по формуле

${\overline {I(y)}}={\begin{cases}-{\frac {1}{n}}\sum _{i=1}^{n}{log_{b}{\frac {1}{1+e^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}}}}&y=1,\\-{\frac {1}{n}}\sum _{i=1}^{n}{log_{b}{\frac {e^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}}{1+e^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}}}}&y=0\end{cases}}$,

где $Z_{i}=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{is}$, и $x_{is}$ это $s^{th}$ входные данные для $i^{th}$ наблюдение.

Информационная энтропия для гиперболастичной H1

Информационная энтропия измеряет потерю информации в передаваемом сообщении или сигнале. В приложениях машинного обучения это количество битов, необходимое для передачи случайно выбранного события из распределения вероятностей. Для дискретной случайной величины $Y$, информационная энтропия $H$ определяется как

$H=-\sum _{y\in Y}{P(y)\ {log}_{b}P(y)}$

где $P(y)$ - функция массы вероятности для случайной величины $Y$.

Информационная энтропия – это математическое ожидание $I(y)$ относительно функции массы вероятности $P(y)$. Информационная энтропия имеет множество применений в машинном обучении и искусственном интеллекте, таких как классификационное моделирование и деревья решений. Для гиперболастичной H1 энтропия $H$ равно

${\begin{aligned}H&=-\sum _{y\in \{0,1\}}{P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }})log_{b}(P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }}))}\\&=-[\pi (\mathbf {x} ;{\boldsymbol {\beta }})\ log_{b}(\pi (\mathbf {x} ;{\boldsymbol {\beta }})+(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))log_{b}(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))]\\&={log}_{b}(1+e^{-Z-\theta \operatorname {arsinh} (Z)})-{\frac {e^{-Z-\theta \operatorname {arsinh} (Z)}{log}_{b}(e^{-Z-\theta \operatorname {arsinh} (Z)})}{1+e^{-Z-\theta \operatorname {arsinh} (Z)}}}\end{aligned}}$

Оценочная средняя энтропия для гиперболатического H1 обозначается как ${\bar {H}}$ и дается

${\bar {H}}={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})-}{\frac {e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})}\ {log}_{b}(e^{{-Z}_{i}-\theta \operatorname {arsinh} ((Z_{i})})}{1+e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})}}}]$

Бинарная кросс-энтропия для гиперболатического H1

Двоичная кросс-энтропия сравнивает наблюдаемые $y\in \{0,1\}$ с предсказанными вероятностями. Средняя бинарная кросс-энтропия для гиперболатического H1 обозначается как ${\overline {C}}$ и равен

${\begin{aligned}{\overline {C}}&=-{\frac {1}{n}}\sum _{i=1}^{n}{{[y}_{i}log_{b}(\pi (x_{i};{\boldsymbol {\beta }}))+}{(1-y}_{i})log_{b}(1-\pi (x_{i};{\boldsymbol {\beta }}))]\\&={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})-}{(1-y}_{i})log_{b}(e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})]\end{aligned}}$

Бинарная гиперболатическая регрессия II типа.

Гиперболатическая регрессия типа II — альтернативный метод анализа двоичных данных с устойчивыми свойствами. Для двоичной переменной результата $Y$, гиперболатическая вероятность успеха типа II является функцией $p$-мерный вектор объясняющих переменных $\mathbf {x} _{i}$ данный

$\pi (\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+\operatorname {arsinh} [e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}]}}$ ,

Для бинарной гиперболатической регрессии типа II шансы на успех обозначаются как $Odds_{H2}$ и определяется как

$Odds_{H2}={\frac {1}{\operatorname {arsinh} [e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}]}}.$

Логит-преобразование $L_{H2}$ дается

$L_{H2}=-\log {(\operatorname {arsinh} [e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}])}$

Информация Шеннона для бинарной гиперболастики типа II (H2)

Для бинарной гиперболической регрессии H2 информация Шеннона $I(y)$ дается

$I(y)={\begin{cases}-log_{b}{\frac {1}{1+arsinh(e^{-Z})}}&y=1\\-log_{b}{\frac {arsinh(e^{-Z})}{1+arsinh(e^{-Z})}}&y=0\end{cases}}$

где $Z=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{s}$, и $x_{s}$ это $s^{th}$ входные данные.Для случайной выборки бинарных результатов размером $n$, средняя эмпирическая информация для гиперболастичной H2 оценивается по формуле

${\overline {I(y)}}={\begin{cases}-{\frac {1}{n}}\sum _{i=1}^{n}log_{b}{\frac {1}{1+arsinh(e^{-Z_{i}})}}&y=1\\-{\frac {1}{n}}\sum _{i=1}^{n}log_{b}{\frac {arsinh(e^{-Z_{i}})}{1+arsinh(e^{-Z_{i}})}}&y=0\end{cases}}$

где $Z_{i}=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{is}$, и $x_{is}$ это $s^{th}$ входные данные для $i^{th}$ наблюдение.

Информационная энтропия для гиперболастичной H2

Для гиперболастичной H2 информационная энтропия $H$ равно

${\begin{aligned}H&=-\sum _{y\in \{0,1\}}{P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }})log_{b}(P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }}))}\\&=-[\pi (\mathbf {x} ;{\boldsymbol {\beta }})\ log_{b}(\pi (\mathbf {x} ;{\boldsymbol {\beta }}))+(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))log_{b}(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))]\\&=log_{b}(1+arsinh(e^{-Z}))-{\frac {arsinh(e^{-Z})log_{b}(arsinh(e^{-Z}))}{1+arsinh(e^{-Z})}}\end{aligned}}$

и предполагаемая средняя энтропия ${\bar {H}}$ для гиперболатического H2 есть

${\bar {H}}={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+{arsinh(e}^{{-Z}_{i}}))-}{\frac {{arsinh(e}^{{-Z}_{i}})\ {log}_{b}{(arsinh(e}^{{-Z}_{i}}))}{1+{arsinh(e}^{{-Z}_{i}})}}]$

Бинарная кросс-энтропия для гиперболатического H2

Средняя двоичная кросс-энтропия ${\overline {C}}$ для гиперболатического H2 есть

${\begin{aligned}{\overline {C}}&=-{\frac {1}{n}}\sum _{i=1}^{n}{{[y}_{i}log_{b}(\pi (x_{i};\beta ))+}{(1-y}_{i})log_{b}(1-\pi (x_{i};\beta ))]\\&={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+{arsinh(e}^{{-Z}_{i}}))-}{(1-y}_{i})log_{b}({arsinh(e}^{{-Z}_{i}}))]\end{aligned}}$

Оценка параметров бинарной гиперболатической регрессии I и II типов

Оценка вектора параметров ${\boldsymbol {\beta }}$ может быть получено путем максимизации функции логарифмического правдоподобия

${\hat {\beta }}={\underset {\boldsymbol {\beta }}{\operatorname {argmax} }}{\sum _{i=1}^{n}[y_{i}ln(\pi (\mathbf {x} _{i};{\boldsymbol {\beta }}))+(1-y_{i})ln(1-\pi (\mathbf {x} _{i};{\boldsymbol {\beta }}))]}$

где $\pi (\mathbf {x} _{i};{\boldsymbol {\beta }})$ определяется в соответствии с одним из двух типов используемых гиперболастических функций.

Полиномиальная гиперболатическая регрессия I и II типов.

Обобщение бинарной гиперболатической регрессии до полиномиальной гиперболатической регрессии имеет переменную отклика $y_{i}$ для индивидуального $i$ с $k$ категории (т.е. $y_{i}\in \{1,2,\ldots ,k\}$). Когда $k=2$, эта модель сводится к бинарной гиперболатической регрессии.Для каждого $i=1,2,\ldots ,n$, мы формируем $k$ индикаторные переменные $y_{ij}$ где

$y_{ij}={\begin{cases}1&{\text{if }}y_{i}=j,\\0&{\text{if }}y_{i}\neq j\end{cases}}$,

это означает, что $y_{ij}=1$ всякий раз, когда $i^{th}$ ответ находится в категории $j$ и $0$ в противном случае.

Определить вектор параметров ${\boldsymbol {\beta }}_{j}=(\beta _{j0},\beta _{j1},\ldots ,\beta _{jp})$ в $p+1$-мерное евклидово пространство и ${\boldsymbol {\beta }}=({\boldsymbol {\beta }}_{1},\ldots ,{\boldsymbol {\beta }}_{k-1})^{T}$.

Использование категории 1 в качестве эталона и $\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})$ в качестве соответствующей функции вероятности полиномиальная гиперболатическая регрессия вероятностей типа I определяется как

$\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+\sum _{s=2}^{k}e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatorname {arsinh} [\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}}$

и для $j=2,\ldots ,k$,

$\pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=j|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {e^{-\eta _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatorname {arsinh} [\eta _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}{1+\sum _{s=2}^{k}e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatorname {arsinh} [\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}}$

Аналогично для полиномиальной гиперболатической регрессии типа II имеем

$\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+\sum _{s=2}^{k}arsinh[e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}}$

и для $j=2,\ldots ,k$,

$\pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=j|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {arsinh[e^{-\eta _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}{1+\sum _{s=2}^{k}arsinh[e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}}$

где $\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})=\beta _{s0}+\sum _{l=1}^{p}\beta _{sl}x_{il}$ с $s=2,\dots ,k$ и $i=1,\dots ,n$.

Выбор $\pi _{i}(\mathbf {x_{i}} ;{\boldsymbol {\beta }})$ зависит от выбора гиперболастика H1 или H2.

Информация Шеннона для многоклассового гиперболастика H1 или H2

Для мультикласса $(j=1,2,\dots ,k)$, информация Шеннона $I_{j}$ является

$I_{j}=-log_{b}(\pi _{j}(\mathbf {x} ;{\boldsymbol {\beta }}))$.

Для случайной выборки размером $n$, эмпирическую информацию о мультиклассах можно оценить по формуле

${\overline {I_{j}}}=-{\frac {1}{n}}\sum _{i=1}^{n}{log_{b}(\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }}))}$.

Мультиклассовая энтропия в теории информации

Для дискретной случайной величины $Y$энтропия мультиклассовой информации определяется как

$H=-\sum _{y\in Y}{P(y)\ {log}_{b}P(y)}$

где $P(y)$ - функция массы вероятности для многоклассовой случайной величины $Y$.

Для гиперболатических H1 или H2 мультиклассовая энтропия $H$ равно

$H=-\sum _{j=1}^{k}{[\pi _{j}(\mathbf {x} ;{\boldsymbol {\beta }})log_{b}(\pi _{j}(\mathbf {x} ;{\boldsymbol {\beta }}))]}$

Предполагаемая средняя мультиклассовая энтропия ${\overline {H}}$ равно

${\overline {H}}=-{\frac {1}{n}}\sum _{i=1}^{n}{\sum _{j=1}^{k}{[\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }})log_{b}(\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }}))]}}$

Мультиклассовая кросс-энтропия для гиперболастичных H1 или H2

Кросс-энтропия мультиклассов сравнивает наблюдаемые выходные данные мультикласса с прогнозируемыми вероятностями. Для случайной выборки мультиклассовых результатов размером $n$, средняя мультиклассовая кросс-энтропия ${\overline {C}}$ для гиперболастичных H1 или H2 можно оценить по формуле

${\overline {C}}=-{\frac {1}{n}}\sum _{i=1}^{n}{\sum _{j=1}^{k}{[y_{ij}log_{b}(\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }}))]}}$

Лог-шансы членства в категории $j$ по сравнению с референтной категорией 1, обозначаемой $o_{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})$, равно

$o_{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=ln[{\frac {\pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})}{\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})}}]$

где $j=2,\ldots ,k$ и $i=1,\ldots ,n$. Предполагаемая матрица параметров ${\hat {\boldsymbol {\beta }}}$ полиномиальной гиперболатической регрессии получается путем максимизации логарифмической функции правдоподобия. Оценки максимального правдоподобия матрицы параметров ${\boldsymbol {\beta }}$ является

${\boldsymbol {\hat {\beta }}}={\underset {\boldsymbol {\beta }}{\operatorname {argmax} }}{\sum _{i=1}^{n}(y_{i1}ln[\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})]+y_{i2}ln[\pi _{2}(\mathbf {x} _{i};{\boldsymbol {\beta }})]+\ldots +y_{ik}ln[\pi _{k}(\mathbf {x} _{i};{\boldsymbol {\beta }})])}$