Сигмоидальная функция

Сигмовидная функция -это любая математическая функция которой , график имеет характерную S-образную или сигмоидную кривую .

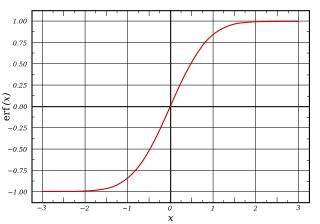
Распространенным примером сигмоидной функции является логистическая функция, показанная на первом рисунке и определяемая формулой: ^{[ 1 ]}

\sigma (x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{1+e^{x}}}=1-\sigma (-x).

Другие стандартные сигмоидные функции приведены в разделе «Примеры» . В некоторых областях, особенно в контексте искусственных нейронных сетей , термин «сигмоидальная функция» используется в качестве псевдонима для логистической функции.

Особые случаи сигмоидной функции включают кривую гомперца (используется в системах моделирования, которые насыщают при больших значениях x) и кривой Ogee (используется в водосточном пути некоторых плотин ). Сигмоидные функции имеют домен всех реальных чисел , причем значение возврата (ответа) обычно монотонно увеличивается , но может уменьшаться. Сигмоидные функции чаще всего показывают возвращаемое значение (ось Y) в диапазоне от 0 до 1. Другой обычно используемый диапазон составляет от -1 до 1.

Широкий спектр сигмоидных функций, включая логистические и гиперболические тангентные функции, использовались в качестве функции активации искусственных нейронов . Сигмоидные кривые также распространены в статистике в качестве совокупных функций распределения (которые переходят от 0 до 1), такие как интегралы логистической плотности , нормальная плотность и -вероятности студента Т функции плотности . Функция логистической сигмоидки инвертируется, а ее обратная функция - функция логита .

Определение

Сигмоидальная функция-это ограниченная , дифференцируемая , реальная функция, которая определена для всех реальных входных значений и имеет неотрицательную производную в каждой точке ^{[ 1 ]} ^{[ 2 ]} И ровно одна точка перегиба .

Характеристики

В целом, сигмоидальная функция является монотонной и имеет первую производную , которая имеет форму колокольчика . И наоборот, интеграл любой непрерывной, неотрицательной, колоколообразной функции (с одним локальным максимумом и без локального минимума, если не вырожденный), будет сигмоидальным. Таким образом, совокупные функции распределения для многих распространенных вероятностных распределений являются сигмоидальными. Одним из таких примеров является функция ошибки , которая связана с совокупной функцией распределения нормального распределения ; Другим является функция Arctan , которая связана с совокупной функцией распределения распределения Коши .

Сигмоидальная функция ограничена парой горизонтальных асимптот как $x\rightarrow \pm \infty$ .

Сигмоидальная функция является выпуклой для значений меньше, чем определенная точка, и она является вогнутой для значений, больше, чем эта точка: во многих примерах здесь эта точка составляет 0.

Примеры

Некоторые сигмоидные функции сравнивали. На чертеже все функции нормализованы таким образом, что их наклон на начале 1.

Логистическая функция $f(x)={\frac {1}{1+e^{-x}}}$
Гиперболическая касательная (смещенная и масштабированная версия логистической функции, выше) $f(x)=\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$
Функция Arctangent $f(x)=\arctan x$
Гудерманнская функция $f(x)=\operatorname {gd} (x)=\int _{0}^{x}{\frac {dt}{\cosh t}}=2\arctan \left(\tanh \left({\frac {x}{2}}\right)\right)$
Функция ошибки $f(x)=\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt$
Обобщенная логистическая функция $f(x)=\left(1+e^{-x}\right)^{-\alpha },\quad \alpha >0$
Плавная функция $f(x)={\begin{cases}{\displaystyle \left(\int _{0}^{1}\left(1-u^{2}\right)^{N}du\right)^{-1}\int _{0}^{x}\left(1-u^{2}\right)^{N}\ du},&|x|\leq 1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\quad N\in \mathbb {Z} \geq 1$
Некоторые алгебраические функции , например, $f(x)={\frac {x}{\sqrt {1+x^{2}}}}$
И в более общей форме ^{[ 3 ]} $f(x)={\frac {x}{\left(1+|x|^{k}\right)^{1/k}}}$
До смен и масштабирования многие сигмоиды являются особыми случаями $f(x)=\varphi (\varphi (x,\beta ),\alpha ),$ где $\varphi (x,\lambda )={\begin{cases}(1-\lambda x)^{1/\lambda }&\lambda \neq 0\\e^{-x}&\lambda =0\\\end{cases}}$ является обратным отрицательным преобразованием коробки -кокса , и $\alpha <1$ и $\beta <1$ параметры формы. ^{[ 4 ]}
Функция плавного перехода ^{[ 5 ]} нормализован по (-1,1):

${\begin{aligned}f(x)&={\begin{cases}{\displaystyle {\frac {2}{1+e^{-2m{\frac {x}{1-x^{2}}}}}}-1},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\\&={\begin{cases}{\displaystyle \tanh \left(m{\frac {x}{1-x^{2}}}\right)},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\end{aligned}}$ Использование гиперболической касательной, упомянутой выше. Здесь, $m$ это свободный параметр, кодирующий наклон на $x=0$ , который должен быть больше или равен ${\sqrt {3}}$ потому что любое меньшее значение приведет к функции с множественными точками перегиба, что, следовательно, не является истинной сигмоидом. Эта функция необычна, потому что на самом деле она достигает ограничивающих значений -1 и 1 в конечном диапазоне, что означает, что его значение постоянно в -1 для всех $x\leq -1$ и в 1 для всех $x\geq 1$ Полем Тем не менее, он гладкий (бесконечно дифференцируемый, $C^{\infty }$ ) везде , в том числе в $x=\pm 1$ .

Приложения

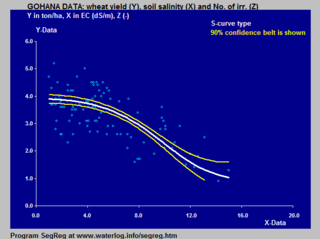
Многие природные процессы, такие как сложные кривые обучения систем , демонстрируют прогрессию от небольших начинаний, которые ускоряются и подходят к кульминации с течением времени. Когда не хватает конкретной математической модели, часто используется сигмоидальная функция. ^{[ 6 ]}

Модель Van Genuchten-Gupta основана на инвертированной S-кривой и применяется к реакции урожайности на соленость почвы .

Примеры применения логистической S-кривой к реакции урожая (пшеница) как на соленость почвы, так и глубину к столу воды в почве показаны при моделировании отклика сельского хозяйства в сельском хозяйстве .

В искусственных нейронных сетях иногда вместо этого используются ненужные функции для эффективности; Они известны как твердые сигмоиды .

При обработке аудиосигнала функции сигмоида используются в качестве WaveShaper функций передачи для эмуляции звука схемы аналоговой обрезки . ^{[ 7 ]}

В биохимии и фармакологии уравнения Хилл Хилл и -Лангмур являются сигмоидными функциями.

В компьютерной графике и рендеринге в реальном времени некоторые из сигмоидных функций используются для смешивания цветов или геометрии между двумя значениями, плавно и без видимых швов или разрывов.

Кривые титрования между сильными кислотами и сильными основаниями имеют сигмоидную форму из -за логарифмической природы шкалы рН .

Логистическая функция может быть эффективно рассчитана с помощью UNUMS типа III . ^{[ 8 ]}

Смотрите также

Функция шага - линейная комбинация функций индикатора реальных интервалов
Функция знака -математическая функция возвращается -1, 0 или 1
Функция Stepiside Step - функция индикатора положительных чисел
Логистическая регрессия - статистическая модель для двоичной зависимой переменной
Logit - функция в статистике
Функция SoftPlus - страницы функций активации
Соболева модифицированная гиперболическая тангентная функция математической активации в анализе данных
Функция Softmax -гладкое приближение однопользового arg max
Функция SWISH - Функция математической активации в анализе данных
Распределение Вейбулла - непрерывное распределение вероятностей
Статистика Ферми -Дирака - статистическое описание поведения фермионов

Ссылки

^ Jump up to: ^а ^{беременный} Хан, Джун; Мораг, Клаудио (1995). «Влияние параметров функции сигмоида на скорость обучения обратном распространении» . В Мира, Хосе; Сандовал, Франциско (ред.). От естественного до искусственных нейронных вычислений . Заметки лекции в информатике. Тол. 930. С. 195–201 . doi : 10.1007/3-540-59497-3_175 . ISBN 978-3-540-59497-0 .
^ Лин, Йибеи; Он, бин (декабрь 1993 г.). «Энтропийный анализ моделей биологического роста» . IEEE транзакции по биомедицинской инженерии . 40 (12): 1193–2000. doi : 10.1109/10.250574 . PMID 8125495 .
^ Даннинг, Эндрю Дж.; Кенслер, Дженнифер; Coudeville, Laurent; Bailleux, Fabrice (2015-12-28). «Некоторые расширения в непрерывных методах иммунологических коррелятов защиты» . Методология медицинских исследований BMC . 15 (107): 107. doi : 10.1186/s12874-015-0096-9 . PMC 4692073 . PMID 26707389 .
^ "Grex --- Explorer роста" . GitHub . 2022-07-09. Архивировано из оригинала 2022-08-25 . Получено 2022-08-25 .
^ Epsilondelta (2022-08-16). «Функция плавного перехода в одном измерении | Функция плавного перехода серии 1» . 13: 29/14: 04 - через www.youtube.com.
^ Гиббс, Марк Н.; Маккей Д. (ноябрь 2000). «Вариационные гауссовые классификаторы». IEEE транзакции в нейронных сетях . 11 (6): 1458–1464. doi : 10.1109/72.883477 . PMID 18249869 . S2CID 14456885 .
^ Смит, Юлий О. (2010). Физическая обработка аудиосигнала (2010 год). W3K Publishing. ISBN 978-0-9745607-2-4 Полем Архивировано из оригинала 2022-07-14 . Получено 2020-03-28 .
^ Густафсон, Джон Л .; Йонемото, Исаак (2017-06-12). «Избиение плавающей запятой в своей собственной игре: позитивная арифметика» (PDF) . Архивировано (PDF) из оригинала на 2022-07-14 . Получено 2019-12-28 .

Дальнейшее чтение

Митчелл, Том М. (1997). Машинное обучение . WCB McGraw - Hill . ISBN 978-0-07-042807-2 Полем Полем (Nb. В частности, см. «Глава 4: Искусственные нейронные сети» (в частности, стр. 96–97), где Митчелл использует слово «логистическая функция» и синоним «сигмоидальной функции» - эта функция также называет «функцию сжимания». -и сигмоидальная (ака логистическая) функция используется для сжатия выходов «нейронов» в многослойных нейронных сетях.)
Хамфрис, Марк. «Непрерывный выход, сигмоидальная функция» . Архивировано из оригинала 2022-07-14 . Получено 2022-07-14 . (NB.

Внешние ссылки

«Подгонка логистических S-кривов (Sigmoids) к данным с использованием Segrega» . Архивировано из оригинала 2022-07-14.

[Han-Morag_1995-1] Jump up to: ^а ^{беременный} Хан, Джун; Мораг, Клаудио (1995). «Влияние параметров функции сигмоида на скорость обучения обратном распространении» . В Мира, Хосе; Сандовал, Франциско (ред.). От естественного до искусственных нейронных вычислений . Заметки лекции в информатике. Тол. 930. С. 195–201 . doi : 10.1007/3-540-59497-3_175 . ISBN 978-3-540-59497-0 .

[yibei-2] Лин, Йибеи; Он, бин (декабрь 1993 г.). «Энтропийный анализ моделей биологического роста» . IEEE транзакции по биомедицинской инженерии . 40 (12): 1193–2000. doi : 10.1109/10.250574 . PMID 8125495 .

[Dunning-Kensler-Coudeville-Bailleux_2015-3] Даннинг, Эндрю Дж.; Кенслер, Дженнифер; Coudeville, Laurent; Bailleux, Fabrice (2015-12-28). «Некоторые расширения в непрерывных методах иммунологических коррелятов защиты» . Методология медицинских исследований BMC . 15 (107): 107. doi : 10.1186/s12874-015-0096-9 . PMC 4692073 . PMID 26707389 .

[grex-4] "Grex --- Explorer роста" . GitHub . 2022-07-09. Архивировано из оригинала 2022-08-25 . Получено 2022-08-25 .

[5] Epsilondelta (2022-08-16). «Функция плавного перехода в одном измерении | Функция плавного перехода серии 1» . 13: 29/14: 04 - через www.youtube.com.

[Gibbs_2000-6] Гиббс, Марк Н.; Маккей Д. (ноябрь 2000). «Вариационные гауссовые классификаторы». IEEE транзакции в нейронных сетях . 11 (6): 1458–1464. doi : 10.1109/72.883477 . PMID 18249869 . S2CID 14456885 .

[Smith_2010-7] Смит, Юлий О. (2010). Физическая обработка аудиосигнала (2010 год). W3K Publishing. ISBN 978-0-9745607-2-4 Полем Архивировано из оригинала 2022-07-14 . Получено 2020-03-28 .

[Gustafson-Yonemoto_2017-8] Густафсон, Джон Л .; Йонемото, Исаак (2017-06-12). «Избиение плавающей запятой в своей собственной игре: позитивная арифметика» (PDF) . Архивировано (PDF) из оригинала на 2022-07-14 . Получено 2019-12-28 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]