Обратные гиперболические функции

Графики обратных гиперболических функций

Гиперболические функции sinh , cosh и tanh относительно единичной гиперболы аналогичны круговым функциям sin , cos , tan относительно единичной окружности. Аргументом гиперболических функций является гиперболическая угловая мера.

В математике обратные гиперболические функции являются обратными гиперболическими функциями , аналогичными обратным круговым функциям . Обычно используются шесть: обратный гиперболический синус, обратный гиперболический косинус, обратный гиперболический тангенс, обратный гиперболический косеканс, обратный гиперболический секанс и обратный гиперболический котангенс. Их обычно обозначают символами гиперболических функций с префиксом arc- или ar- .

Для данного значения гиперболической функции обратная гиперболическая функция обеспечивает соответствующую меру гиперболического угла , например $\operatorname {arsinh} (\sinh a)=a$ и $\sinh(\operatorname {arsinh} x)=x.$ Гиперболическая мера угла - это длина дуги единичной гиперболы. $x^{2}-y^{2}=1$ измеренная в лоренцевой плоскости ( а не длина гиперболической дуги в евклидовой плоскости ), и удвоенная площадь соответствующего гиперболического сектора . Это аналогично тому, как мерой кругового угла является длина дуги единичной окружности в евклидовой плоскости или удвоенная площадь соответствующего кругового сектора . Альтернативно гиперболический угол - это площадь сектора гиперболы. $xy=1.$ Некоторые авторы называют обратные гиперболические функции гиперболическими площадными функциями .

Гиперболические функции встречаются при вычислении углов и расстояний в гиперболической геометрии . Это также происходит в решениях многих линейных дифференциальных уравнений (таких как уравнение, определяющее цепную линию ), кубических уравнений и уравнения Лапласа в декартовых координатах . Уравнения Лапласа важны во многих областях физики , включая теорию электромагнетизма , теплообмен , гидродинамику и специальную теорию относительности .

Обозначения

Луч, проходящий через единичную гиперболу $x^{2}\ -\ y^{2}\ =\ 1$ в точку $(\cosh \,a,\,\sinh \,a)$, где $a$ в два раза больше площади между лучом, гиперболой и $x$-ось

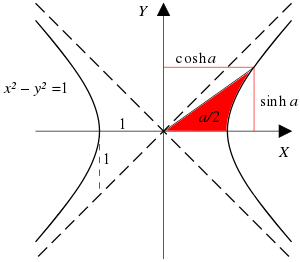
Самые ранние и наиболее широко распространенные символы используют префикс arc- (то есть: arcsinh , arccosh , arctanh , arcsech , arccsch , arccoth ), по аналогии с обратными круговыми функциями ( arcsin и т. д.). Для единичной гиперболы («лоренцева окружность») в лоренцевой плоскости ( псевклидова плоскость ( сигнатуры 1, 1) ) или в гиперболической числовой плоскости, мера гиперболического угла (аргумент гиперболических функций) действительно является длиной гиперболической дуги.

Также распространено обозначение $\sinh ^{-1},$ $\cosh ^{-1},$ и т. д., хотя необходимо проявлять осторожность, чтобы избежать неправильной интерпретации верхнего индекса -1 как показателя степени. Стандартное соглашение заключается в том, что $\sinh ^{-1}x$ или $\sinh ^{-1}(x)$ означает обратную функцию, а $(\sinh x)^{-1}$ или $\sinh(x)^{-1}$ означает взаимное $1/\sinh x.$ Особенно непоследовательным является традиционное использование верхних индексов положительных целых чисел для обозначения показателя степени, а не композиции функции, например $\sinh ^{2}x$ условно означает $(\sinh x)^{2}$ и не $\sinh(\sinh x).$

Поскольку аргументом гиперболических функций не является длина гиперболической дуги в евклидовой плоскости , некоторые авторы осудили префикс arc- , утверждая, что префикс ar- (для площади ) или arg- (для аргумента ) должен быть предпочтительнее. Следуя этой рекомендации, стандартные сокращения ISO 80000-2 используют префикс ar- (то есть: arsinh , arcosh , artanh , arsech , arcsch , arcoth ).

В языках программирования обратные круговые и гиперболические функции часто называются с более коротким префиксом a- ( asinh и т. д.).

будет последовательно использоваться префикс ar- В этой статье для удобства .

Определения в терминах логарифмов

Поскольку гиперболические функции являются квадратично- рациональными функциями показательной функции $\exp x,$ их можно решить с помощью квадратичной формулы , а затем записать в виде натурального логарифма .

${\begin{aligned}\operatorname {arsinh} x&=\ln \left(x+{\sqrt {x^{2}+1}}\right)&-\infty &<x<\infty ,\\[10mu]\operatorname {arcosh} x&=\ln \left(x+{\sqrt {x^{2}-1}}\right)&1&\leq x<\infty ,\\[10mu]\operatorname {artanh} x&={\frac {1}{2}}\ln {\frac {1+x}{1-x}}&-1&<x<1,\\[10mu]\operatorname {arcsch} x&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)&-\infty &<x<\infty ,\ x\neq 0,\\[10mu]\operatorname {arsech} x&=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)&0&<x\leq 1,\\[10mu]\operatorname {arcoth} x&={\frac {1}{2}}\ln {\frac {x+1}{x-1}}&-\infty &<x<-1\ \ {\text{or}}\ \ 1<x<\infty .\end{aligned}}$

Для комплексных аргументов обратные круговые и гиперболические функции, квадратный корень и натуральный логарифм являются многозначными функциями .

Формулы сложения

$\operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)$

$\operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)$

$\operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)$

$\operatorname {arcoth} u\pm \operatorname {arcoth} v=\operatorname {arcoth} \left({\frac {1\pm uv}{u\pm v}}\right)$

${\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}$

Другие личности

${\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ for }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ for }}x\geq 1\\2\operatorname {arsinh} x&=\operatorname {arcosh} (2x^{2}+1)&\quad {\hbox{ for }}x\geq 0\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ for }}x\geq 0\end{aligned}}$

$\ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)$

Композиция гиперболических и обратных гиперболических функций

${\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{for}}\quad |x|>1\\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\sqrt {1-x^{2}}}}\quad {\text{for}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{\sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad {\text{for}}\quad |x|>1\end{aligned}}$

Композиция обратных гиперболических и круговых функций

$\operatorname {arsinh} \left(\tan \alpha \right)=\operatorname {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha }{\cos \alpha }}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\cos \alpha }}\right)$

$\ln \left(\left|\tan \alpha \right|\right)=-\operatorname {artanh} \left(\cos 2\alpha \right)$

Конверсии

$\ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)$

$\operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\sqrt {1-x^{2}}}}\right)$

$\operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\sqrt {1+x^{2}}}\right)$

$\operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \left({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|$

Производные

${\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{\text{ for all real }}x\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}},{\text{ for all real }}x>1\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|<1\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2}}},{\text{ for all real }}|x|>1\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ for all real }}x\in (0,1)\\{\frac {d}{dx}}\operatorname {arcsch} x&{}={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ for all real }}x{\text{, except }}0\\\end{aligned}}$

Эти формулы можно вывести через производные гиперболических функций. Например, если $x=\sinh \theta$, затем ${\textstyle dx/d\theta =\cosh \theta ={\sqrt {1+x^{2}}},}$ так

${\frac {d}{dx}}\operatorname {arsinh} (x)={\frac {d\theta }{dx}}={\frac {1}{dx/d\theta }}={\frac {1}{\sqrt {1+x^{2}}}}.$

Расширения серии

Для вышеуказанных функций можно получить ряд расширения:

${\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

${\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}$

${\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}$

${\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

${\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}$

${\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}$

Асимптотическое разложение для арсинха имеет вид

$\operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}$

Главные значения в комплексной плоскости

Как функции комплексной переменной , обратные гиперболические функции являются многозначными функциями , которые являются аналитическими , за исключением конечного числа точек. Для такой функции обычно определяют главное значение , которое представляет собой однозначную аналитическую функцию, совпадающую с одной конкретной ветвью многозначной функции, в области, состоящей из комплексной плоскости , в которой конечное число дуг (обычно половина линии или сегменты линий ) были удалены. Эти дуги называются разрезами ветвей . Для указания ветви, то есть определения того, какое значение многозначной функции рассматривается в каждой точке, обычно определяют ее в конкретной точке и выводят значение всюду в области определения главного значения путем аналитического продолжения . Когда это возможно, лучше определить главное значение напрямую, не обращаясь к аналитическому продолжению.

Например, для квадратного корня главное значение определяется как квадратный корень, имеющий положительную действительную часть . Это определяет однозначную аналитическую функцию, которая определена везде, за исключением неположительных действительных значений переменных (где два квадратных корня имеют нулевую действительную часть). Это главное значение функции квадратного корня обозначается ${\sqrt {x}}$ в дальнейшем. Аналогично главное значение логарифма, обозначаемое $\operatorname {Log}$ в дальнейшем определяется как значение, при котором мнимая часть имеет наименьшее абсолютное значение. Он определен везде, кроме неположительных действительных значений переменной, для которых два разных значения логарифма достигают минимума.

Для всех обратных гиперболических функций главное значение может быть определено через главные значения квадратного корня и функции логарифма. Однако в некоторых случаях формулы § Определения в терминах логарифмов не дают правильного главного значения, поскольку дают слишком маленькую область определения и, в одном случае, несвязную .

значение обратного

Главное значение обратного гиперболического синуса определяется выражением

$\operatorname {arsinh} z=\operatorname {Log} (z+{\sqrt {z^{2}+1}}\,)\,.$

Аргумент квадратного корня является неположительным действительным числом тогда и только тогда, когда z принадлежит одному из интервалов [ i , + i ∞) и (− i ∞, − i ] мнимой оси. логарифм вещественный, то он положителен. Таким образом, эта формула определяет главное значение для arsinh с разрезами ветвей [ i , + i ∞) и (− i ∞, − i ] . Это оптимально, поскольку разрезы ветвей должны соединяться. особые точки i и − i до бесконечности.

гиперболического

Формула для обратного гиперболического косинуса, приведенная в § Обратный гиперболический косинус , неудобна, поскольку, как и в случае с главными значениями логарифма и квадратного корня, главное значение arcosh не будет определено для мнимого z . Таким образом, квадратный корень должен быть факторизован, что приводит к

$\operatorname {arcosh} z=\operatorname {Log} (z+{\sqrt {z+1}}{\sqrt {z-1}}\,)\,.$

Оба главных значения квадратных корней определены, за исключением случаев, когда z принадлежит вещественному интервалу (−∞, 1] . Если аргумент логарифма веществен, то z веществен и имеет тот же знак. Таким образом, приведенная выше формула определяет главное значение arcosh вне вещественного интервала (−∞, 1] , который, таким образом, является уникальным разрезом ветвления.

обратного гиперболического тангенса

Формулы, приведенные в § Определения в логарифмах, предполагают

${\begin{aligned}\operatorname {artanh} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {1+z}{1-z}}\right)\\\operatorname {arcoth} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {z+1}{z-1}}\right)\end{aligned}}$

для определения главных значений обратного гиперболического тангенса и котангенса. В этих формулах аргумент логарифма действителен тогда и только тогда, когда z действительно. Для artanh этот аргумент находится в вещественном интервале (−∞, 0] , если z принадлежит либо (−∞, −1] либо [1, ∞) . Для arcoth аргумент логарифма находится в (−∞ , 0] тогда и только тогда, когда z принадлежит вещественному интервалу [−1, 1] .

Следовательно, эти формулы определяют удобные главные значения, для которых разрезами ветвей являются (−∞, −1] и [1, ∞) для обратного гиперболического тангенса и [−1, 1] для обратного гиперболического котангенса.

Ввиду лучшей численной оценки вблизи срезов ветвей некоторые авторы используйте следующие определения главных значений, хотя второе вводит устранимую особенность при z = 0 . Два определения $\operatorname {artanh}$ различаются по реальным значениям $z$ с $z>1$. Те из $\operatorname {arcoth}$ различаются по реальным значениям $z$ с $z\in [0,1)$.

${\begin{aligned}\operatorname {artanh} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+z}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-z}\right)\\\operatorname {arcoth} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+{\frac {1}{z}}}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-{\frac {1}{z}}}\right)\end{aligned}}$

косеканса

Для обратного гиперболического косеканса главное значение определяется как

$\operatorname {arcsch} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}+1}}\,\right)$.

Он определен, за исключением случаев, когда аргументы логарифма и квадратного корня являются неположительными действительными числами. Таким образом, главное значение квадратного корня определяется вне интервала [− i , i ] воображаемой прямой. Если аргумент логарифма вещественный, то z — ненулевое действительное число, а это означает, что аргумент логарифма положителен.

Таким образом, главное значение определяется приведенной выше формулой вне разреза ветвления , состоящего из интервала [− i , i ] мнимой прямой.

(При z = 0 существует особая точка, которая входит в разрез ветвления.)

гиперболического секанса

Здесь, как и в случае с обратным гиперболическим косинусом, нам необходимо факторизовать квадратный корень. Это дает главное значение

$\operatorname {arsech} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z}}+1}}\,{\sqrt {{\frac {1}{z}}-1}}\right).$

Если аргумент квадратного корня действителен, то z действителен, и отсюда следует, что оба главных значения квадратных корней определены, за исключением случаев, когда z действителен и принадлежит одному из интервалов (−∞, 0] и [1, +∞) . Если аргумент логарифма вещественный и отрицательный, то z также вещественный и отрицательный. Отсюда следует, что главное значение arsech корректно определяется приведенной выше формулой вне двух разрезов ветвей , вещественных интервалов (−∞, 0] и [1, +∞) .

При z = 0 существует особая точка, входящая в один из разрезов ветвления.

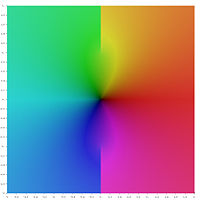
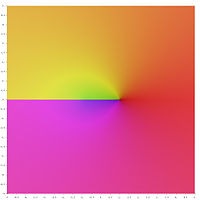
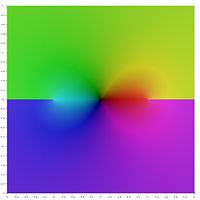
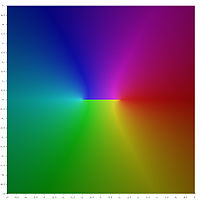
Графическое представление

В следующем графическом представлении главных значений обратных гиперболических функций разрезы ветвей выглядят как разрывы цвета. Тот факт, что все разрезы ветвей выглядят как разрывы, показывает, что эти главные значения нельзя расширить до аналитических функций, определенных в более крупных областях. Другими словами, определенные выше разрезы ветвей минимальны.

$\operatorname {arsinh} (z)$

$\operatorname {arcosh} (z)$

$\operatorname {artanh} (z)$

$\operatorname {arcoth} (z)$

$\operatorname {arsech} (z)$

$\operatorname {arcsch} (z)$

Обратные гиперболические функции в комплексной плоскости z: цвет в каждой точке плоскости представляет комплексное значение соответствующей функции в этой точке.

См. также

• Комплексный логарифм
• Гиперболическое секансное распределение
• ИСО 80000-2
• Список интегралов от обратных гиперболических функций

Библиография

• Герберт Буземанн и Пол Дж. Келли (1953) Проективная геометрия и проективная метрика , стр. 207, Academic Press .

Внешние ссылки

• «Обратные гиперболические функции» , Математическая энциклопедия , EMS Press , 2001 [1994]