Атмосферная рефракция

Не путать с атмосферной дифракцией .

Диаграмма, показывающая смещение изображения Солнца на восходе и закате.

Атмосферная рефракция — это отклонение света или другой электромагнитной волны от прямой линии при прохождении через атмосферу из-за изменения плотности воздуха в зависимости от высоты . Это преломление происходит из-за того, что скорость света в воздухе уменьшается ( показатель преломления увеличивается) с увеличением плотности. Атмосферная рефракция вблизи земли порождает миражи . Такая рефракция может также поднимать или опускать , растягивать или укорачивать изображения удаленных объектов, не затрагивая миражей. Турбулентный воздух может заставить отдаленные объекты мерцать или мерцать . Этот термин также применим к преломлению звука . Атмосферная рефракция учитывается при измерении положения как небесных, так и земных объектов.

Астрономическая или небесная рефракция приводит к тому, что астрономические объекты кажутся над горизонтом выше, чем они есть на самом деле. Земная рефракция обычно приводит к тому, что земные объекты кажутся выше, чем они есть на самом деле, хотя днем, когда воздух у земли нагревается, лучи могут изгибаться вверх, в результате чего объекты кажутся ниже, чем они есть на самом деле.

Преломление влияет не только на видимые световые лучи, но и на все электромагнитное излучение , хотя и в разной степени. Например, в видимом спектре синий цвет более подвержен влиянию, чем красный. Это может привести к тому, что астрономические объекты будут выглядеть рассредоточенными по спектру на изображениях с высоким разрешением.

Атмосфера преломляет изображение растущей , Луны заходящей за горизонт.

По возможности астрономы будут планировать свои наблюдения на периоды кульминации , когда небесные объекты находятся выше всего в небе. Точно так же моряки не будут снимать звезду ниже 20° над горизонтом. Если нельзя избежать наблюдений объектов вблизи горизонта, можно оснастить оптический телескоп системами управления для компенсации смещения, вызванного рефракцией. Если дисперсия также является проблемой (в случае широкополосных наблюдений с высоким разрешением), корректоры атмосферной рефракции (сделанные из пар вращающихся стеклянных призм можно также использовать ).

Поскольку величина атмосферной рефракции является функцией температурного градиента , температуры , давления и влажности (количества водяного пара , что особенно важно на длинах волн среднего инфракрасного диапазона ), количество усилий, необходимых для успешной компенсации, может быть непомерно высоким. . С другой стороны, геодезисты часто планируют свои наблюдения во второй половине дня, когда величина рефракции минимальна.

Атмосферная рефракция становится более сильной при сильных градиентах температуры, а рефракция не является однородной, когда атмосфера неоднородна, например, когда турбулентность в воздухе возникает . Это приводит к неоптимальным условиям наблюдения , таким как мерцание звезд закатом и различные деформации видимой формы Солнца вскоре перед или после восхода солнца .

Астрономическая рефракция

Атмосферная рефракция искажает солнечный диск, придавая ему неровную форму, когда он садится за нижний горизонт.

Астрономическая рефракция связана с угловым положением небесных тел, их внешним видом как точечного источника и, посредством дифференциальной рефракции, с формой протяженных тел, таких как Солнце и Луна.

Атмосферное преломление света звезды равно нулю в зените , менее 1 ′ (одна угловая минута 45 ° ) на видимой высоте и всего лишь 5,3 ′ на высоте 10 °; она быстро увеличивается с уменьшением высоты, достигая 9,9′ на высоте 5°, 18,4′ на высоте 2° и 35,4′ на горизонте ; все значения указаны для 10 °C и 1013,25 гПа. в видимой части спектра.

На горизонте рефракция немного превышает видимый диаметр Солнца, поэтому, когда кажется, что нижняя часть солнечного диска касается горизонта, истинная высота Солнца отрицательна. Если бы в этот момент атмосфера внезапно исчезла, то нельзя было бы увидеть солнце, так как оно было бы полностью за горизонтом. По соглашению, восход и закат относятся к времени, когда верхний край Солнца появляется на горизонте или исчезает с него, а стандартное значение истинной высоты Солнца составляет −50′: −34′ для рефракции и −16′ для полусвета Солнца. -диаметр . Высоту небесного тела обычно принимают за центр диска тела. В случае с Луной Луны необходимы дополнительные поправки на горизонтальный параллакс и ее видимый полудиаметр; оба изменяются в зависимости от расстояния Земля-Луна.

Рефракция вблизи горизонта сильно варьируется, главным образом из-за изменчивости градиента температуры вблизи поверхности Земли и геометрической чувствительности почти горизонтальных лучей к этой изменчивости. Еще в 1830 году Фридрих Бессель обнаружил, что даже после применения всех поправок на температуру и давление (но не на градиент температуры) у наблюдателя высокоточные измерения рефракции изменялись на ±0,19' на высоте двух градусов над горизонтом и на ±0,19'. 0,50 фута на высоте полградуса над горизонтом. На уровне горизонта и ниже значения рефракции, значительно превышающие номинальное значение 35,4 ', наблюдались в широком диапазоне климатических условий. Георг Константин Бурис измерил преломление звезд на горизонте в 4° в Афинской обсерватории. а во время своей злополучной экспедиции на «Эндьюранс » сэр Эрнест Шеклтон зафиксировал рефракцию 2°37′:

«Солнце, которое семь дней назад «появилось в последний раз» семь дней назад, удивило нас, подняв более половины своего диска над горизонтом 8 мая. Зарево на северном горизонте растворилось в солнце в 11 часов утра того дня. Через четверть часа неразумный гость снова исчез, только чтобы снова подняться в 11:40, зайти в 13:00, подняться в 13:10 и медленно зайти в 13:20. Эти любопытные явления были вызваны рефракцией, которая в 13:20 составила 2°37′. Температура была на 15° ниже 0° по Фаренгейту, и мы подсчитали, что рефракция была на 2° выше нормы».

Ежедневные изменения погоды будут влиять на точное время восхода и захода солнца. а также восход и заход луны, и по этой причине обычно не имеет смысла задавать и устанавливать время с большей точностью, чем ближайшая минута. Более точные расчеты могут быть полезны для определения ежедневных изменений времени нарастания и захода солнца, которые могут произойти при стандартном значении рефракции. если понимать, что фактические изменения могут отличаться из-за непредсказуемых изменений рефракции.

Поскольку атмосферная рефракция номинально составляет 34 ′ на горизонте, но только 29 ′ на высоте 0,5 ° над ним, заходящее или восходящее солнце кажется сплющенным примерно на 5 ′ (около 1/6 его видимого диаметра).

Расчет рефракции

Молодой выделил несколько регионов, где были применимы разные методы расчета астрономической рефракции. В верхней части неба, при зенитном расстоянии менее 70° (или высоте более 20°), применяются различные простые формулы преломления, основанные на показателе преломления (а значит, и на температуре, давлении и влажности) на наблюдатель адекватный. Между 20° и 5° горизонта градиент температуры становится доминирующим фактором, и для численного интегрирования используют такой метод, как метод Ауэра и Стэндиша. и требуется использование температурного градиента стандартной атмосферы и измеренных условий у наблюдателя. Ближе к горизонту при численном интегрировании необходимо использовать фактические измерения изменений высоты локального градиента температуры. Ниже астрономического горизонта рефракция настолько изменчива, что можно сделать лишь приблизительные оценки астрономической рефракции; например, наблюдаемое время восхода или захода солнца может меняться изо дня в день на несколько минут. Как отмечает «Морской альманах» , «действительные значения… рефракции на малых высотах могут в экстремальных атмосферных условиях значительно отличаться от средних значений, использованных в таблицах».

График зависимости рефракции от высоты с использованием формулы Беннета 1982 года.

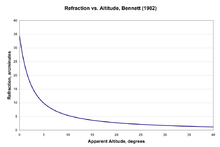
Для расчета астрономической рефракции было разработано множество различных формул; они достаточно последовательны, различаются между собой на несколько угловых минут на горизонте и становятся все более согласованными по мере приближения к зениту. Более простые формулировки включали не что иное, как температуру и давление у наблюдателя, степень котангенса видимой высоты астрономического тела и, в терминах более высокого порядка, высоту вымышленной однородной атмосферы. Самая простая версия этой формулы, которую Смарт считал точной только в пределах 45 ° от зенита, выглядит следующим образом:

$R=(n_{0}-1)\cot h_{\mathrm {a} }\,,$

где R — рефракция в радианах , n ₀ — показатель преломления у наблюдателя (который зависит от температуры, давления и влажности), а h _a — видимый угол высоты астрономического тела.

Раннее простое приближение этой формы, которое напрямую учитывало температуру и давление наблюдателя, было разработано Джорджем Комстоком :

$R={\frac {21.5b}{273+t}}\cot h_{\mathrm {a} }\,,$

где R — рефракция в угловых секундах, b — атмосферное давление в миллиметрах ртутного столба , а t — температура в Цельсиях . Комсток считал, что эта формула дает результаты в пределах одной угловой секунды от значений Бесселя для рефракции от 15 ° над горизонтом до зенита.

Дальнейшее разложение котангенса кажущейся высоты в третьей степени включает в себя H ₀ , высоту однородной атмосферы , в дополнение к обычным условиям для наблюдателя:

$R=(n_{0}-1)(1-H_{0})\cot h_{\mathrm {a} }-(n_{0}-1)[H_{0}-{\frac {1}{2}}(n_{0}-1)]\cot ^{3}h_{\mathrm {a} }.$

Версия этой формулы используется в Международного астрономического союза Стандартах фундаментальной астрономии ; Сравнение алгоритма IAU с более строгими процедурами трассировки лучей показало согласие в пределах 60 миллисекунд дуги на высоте более 15 °.

Беннетт разработал еще одну простую эмпирическую формулу для расчета рефракции по видимой высоте, которая дает рефракцию R в угловых минутах:

$R=\cot \left(h_{\mathrm {a} }+{\frac {7.31}{h_{\mathrm {a} }+4.4}}\right)\,.$

Эта формула используется в США Военно-морской обсерватории программном обеспечении векторной астрометрии . и, как сообщается, согласуется с мнением Гарфинкеля. более сложный алгоритм в пределах 0,07′ на всем диапазоне от зенита до горизонта. Сэмундссон разработал обратную формулу для определения рефракции по истинной высоте; если h — истинная высота в градусах, рефракция R в угловых минутах определяется выражением

$R=1.02\cot \left(h+{\frac {10.3}{h+5.11}}\right)\,;$

формула согласуется с формулой Беннета с точностью до 0,1 '. Формулы Беннета и Сэмундссона предполагают атмосферное давление 101,0 кПа и температуру 10 °С; для разных давлений P и температуры T рассчитанная по этим формулам рефракция умножается на

${\frac {P}{101}}\,{\frac {283}{273+T}}$

Рефракция увеличивается примерно на 1% при каждом увеличении давления на 0,9 кПа и уменьшается примерно на 1% при каждом уменьшении давления на 0,9 кПа. Аналогично, рефракция увеличивается примерно на 1% на каждые понижение температуры на 3 °C и уменьшается примерно на 1% на каждые повышения температуры на 3 °C.

Эффекты случайного преломления

Анимированное изображение поверхности Луны показывает влияние атмосферной турбулентности на вид.

Турбулентность в атмосфере Земли рассеивает свет звезд, делая их то ярче, то тусклее в масштабе миллисекунд . Самые медленные компоненты этих колебаний видны как мерцание (также называемое сцинтилляцией ).

Турбулентность также вызывает небольшие спорадические движения изображения звезды и приводит к быстрым искажениям его структуры. Эти эффекты не видны невооруженным глазом , но их легко увидеть даже в небольшие телескопы. Они нарушают условия астрономического наблюдения . Некоторые телескопы используют адаптивную оптику, чтобы уменьшить этот эффект.

Земная рефракция

Дополнительная информация: Выравнивание рефракции.

Земная рефракция , иногда называемая геодезической рефракцией , связана с видимым угловым положением и измеренным расстоянием до земных тел. Особое внимание уделяется производству точных карт и обзоров . Поскольку луч зрения при земной рефракции проходит вблизи земной поверхности, то величина рефракции зависит главным образом от градиента температуры у земли, который сильно меняется в различное время суток, времена года, характер местности, состояние погоды и других факторов.

В общем приближении земная рефракция рассматривается как постоянное искривление луча света или луча зрения, при котором луч можно рассматривать как описывающий круговой путь. Общей мерой преломления является коэффициент преломления. К сожалению, существуют два разных определения этого коэффициента. Одним из них является отношение радиуса Земли к радиусу луча зрения, другой - это отношение угла, который образует луч зрения в центре Земли, к углу преломления, измеренному у наблюдателя. Поскольку последнее определение измеряет изгиб луча только на одном конце луча зрения, оно вдвое меньше значения первого определения.

Коэффициент преломления напрямую связан с местным вертикальным градиентом температуры, а также с атмосферной температурой и давлением. Увеличенная версия коэффициента k , измеряющего отношение радиуса Земли к радиусу луча зрения, определяется выражением:

$k=503{\frac {P}{T^{2}}}\left(0.0343+{\frac {dT}{dh}}\right),$

где температура T указана в кельвинах , давление P в миллибарах и высота h в метрах. Угол преломления увеличивается с увеличением коэффициента преломления и длины луча зрения.

Хотя прямая линия от вашего глаза до далекой горы может быть перекрыта более близким холмом, луч может изогнуться достаточно, чтобы сделать видимой далекую вершину. Удобный метод анализа влияния рефракции на видимость состоит в рассмотрении увеличенного эффективного радиуса Земли R _eff , определяемого выражением

$R_{\text{eff}}={\frac {R}{1-k}},$

где R — радиус Земли, а k — коэффициент преломления. Согласно этой модели луч можно рассматривать как прямую линию на Земле увеличенного радиуса.

Кривизну преломленного луча в угловых секундах на метр можно вычислить по соотношению

${\frac {1}{\sigma }}=16.3{\frac {P}{T^{2}}}\left(0.0342+{\frac {dT}{dh}}\right)\cos \beta$

где 1/σ — кривизна луча в угловых секундах на метр, P — давление в миллибарах, T — температура в кельвинах, а β — угол луча к горизонту. Умножение половины кривизны на длину пути луча дает угол преломления в наблюдателе. Для луча зрения вблизи горизонта cos β мало отличается от единицы и им можно пренебречь. Это дает

$\Omega =8.15{\frac {LP}{T^{2}}}\left(0.0342+{\frac {dT}{dh}}\right),$

где L — длина луча зрения в метрах, а Ω — рефракция наблюдателя, измеряемая в угловых секундах.

Простое приближение состоит в том, что видимая высота горы на вашем глазу (в градусах) будет превышать ее истинную высоту на расстояние в километрах, разделенное на 1500. Это предполагает достаточно горизонтальную линию обзора и обычную плотность воздуха; если гора очень высокая (большая часть линии обзора находится в разреженном воздухе), вместо этого разделите значение на 1600.

См. также

• Полярный круг#Эффект атмосферной рефракции
• Звуковые волны, на которые влияют изменения плотности воздуха, приводят к атмосферной фокусировке .
• Воздушная масса (астрономия)
• Атмосферная оптика
• Электромагнитное излучение
• Фата Моргана (мираж)
• Ибн аль-Хайсам
• Надвигающиеся и подобные явления рефракции
• Novaya Zemlya effect
• Распространение радио
• Распространение по прямой видимости # Атмосферная рефракция
• Трассировка лучей (физика)
• Шен Куо
• Земная атмосферная линза

Дальнейшее чтение

• Лен, Вальдемар Х.; ван дер Верф, Зибрен (2005). «Атмосферная рефракция: история». Прикладная оптика . 44 (27): 5624–5636. Бибкод : 2005ApOpt..44.5624L . дои : 10.1364/AO.44.005624 . ISSN   0003-6935 . ПМИД   16201423 .
• Филиппенко, А.В. (1982). «Важность атмосферной дифференциальной рефракции в спектрофотометрии» . Опубл. Астрон. Соц. Пак . 94 : 715–721. Бибкод : 1982PASP...94..715F . дои : 10.1086/131052 .
• Хотин, Мартин (1969), «Атмосферная рефракция» , Математическая геодезия , Монография ESSA, том. 2, Вашингтон, округ Колумбия: Министерство торговли США, Управление служб экологических наук, Бибкод : 1969mage.book.....H
• Ненер, Бретт Д.; Фаукс, Невилл; Борредон, Лоран (2003), «Аналитическая модель оптической рефракции в тропосфере», J. Opt. Соц. Являюсь. , 20 (5): 867–875, Bibcode : 2003JOSAA..20..867N , doi : 10.1364/JOSAA.20.000867 , PMID   12747434 , S2CID   21222910
• Томас, Майкл Э.; Джозеф, Ричард И. (1996), «Астрономическая рефракция» (PDF) , Технический дайджест Johns Hopkins APL , 17 : 279–284
• Ван, Ю (20 марта 1998 г.), Белый, Пьер Ю; Брекинридж, Джеймс Б. (ред.), «Космический телескоп очень высокого разрешения, использующий земную атмосферу в качестве объектива», Космические телескопы и инструменты V , 3356 , Лаборатория реактивного движения : 665, Бибкод : 1998SPIE.3356..665W , doi : 10.1117/12.324434 , hdl : 2014/19082 , S2CID   120030054
• Киппинг, Дэвид (18 июля 2019 г.), «Терраскоп: о возможности использования Земли в качестве атмосферной линзы», Публикации Тихоокеанского астрономического общества , 131 (1005), Колумбийский университет : 114503, arXiv : 1908.00490 , Bibcode : 2019PASP..131k4503K , doi : 10.1088/1538-3873/ab33c0 , S2CID   199064594

Внешние ссылки

• Янг, Эндрю Т., Аннотированная библиография миражей, зеленых вспышек, атмосферной рефракции и т. д. , получено 3 мая 2016 г.
• Янг, Эндрю Т., Астрономическая рефракция , получено 3 мая 2016 г.