Потенциальная скважина

Типичная потенциальная энергетическая скважина.

Потенциальная яма — это область, окружающая локальный минимум потенциальной энергии . Энергия, захваченная в потенциальной яме, не может преобразоваться в другой тип энергии ( кинетическую энергию в случае гравитационной потенциальной ямы), поскольку она захватывается в локальном минимуме потенциальной ямы. Следовательно, тело не может перейти к глобальному минимуму потенциальной энергии, как оно естественным образом стремилось бы сделать из-за энтропии .

Обзор

Энергия может высвободиться из потенциальной ямы, если в систему добавлено достаточно энергии, чтобы преодолеть локальный максимум. В квантовой физике потенциальная энергия может покидать потенциальную яму без добавления энергии из-за вероятностных характеристик квантовых частиц ; в этих случаях можно представить, что частица туннелирует сквозь стенки потенциальной ямы.

График двумерной функции потенциальной энергии представляет собой поверхность потенциальной энергии , которую можно представить как поверхность Земли в ландшафте холмов и долин. Тогда потенциальный колодец будет представлять собой долину, окруженную со всех сторон возвышенностью, которая, таким образом, может быть заполнена водой (например, озеро ) без утечек воды к другому, более низкому минимуму (например, уровню моря ).

В случае гравитации область вокруг массы представляет собой гравитационную потенциальную яму, если только плотность массы не настолько мала, что приливные силы других масс превышают гравитацию самого тела.

Потенциальный холм является противоположностью потенциальной ямы и представляет собой область, окружающую локальный максимум .

Квантовое ограничение

Квантовое ограничение отвечает за увеличение разницы энергий между энергетическими состояниями и запрещенной зоной, явление, тесно связанное с оптическими и электронными свойствами материалов.

Квантовое ограничение можно наблюдать, если диаметр материала равен длине волны де Бройля электрона волновой функции . Когда материалы настолько малы, их электронные и оптические свойства существенно отличаются от свойств объемных материалов.

Частица ведет себя так, как если бы она была свободной, когда удерживающий размер велик по сравнению с длиной волны частицы. В этом состоянии запрещенная зона остается на исходной энергии из-за состояния непрерывной энергии. Однако по мере того, как ограничивающий размер уменьшается и достигает определенного предела, обычно в наномасштабе, энергетический спектр становится дискретным . В результате ширина запрещенной зоны становится зависимой от размера. По мере уменьшения размера частиц электроны и электронные дырки сближаются, а энергия, необходимая для их активации, увеличивается, что в конечном итоге приводит к синему смещению светового излучения .

В частности, эффект описывает явление, возникающее в результате сжатия электронов и электронных дырок в измерение, приближающееся к критическому квантовому измерению, называемому экситонным радиусом Бора . В текущем применении квантовая точка , такая как небольшая сфера, ограничена тремя измерениями, квантовая проволока ограничена двумя измерениями, а квантовая яма ограничена только одним измерением. Они также известны как нулевые, одно- и двумерные потенциальные ямы соответственно. В этих случаях они относятся к количеству измерений, в которых ограниченная частица может действовать как свободный носитель. См. внешние ссылки ниже, где приведены примеры применения в биотехнологии и технологии солнечных батарей.

Взгляд квантовой механики

См. Также: Частица в ящике.

На электронные и оптические свойства материалов влияют размер и форма. Хорошо зарекомендовавшие себя технические достижения, включая квантовые точки, были получены в результате манипуляций с размерами и исследований для их теоретического подтверждения эффекта квантового ограничения. Основная часть теории заключается в том, что поведение экситона напоминает поведение атома по мере сокращения окружающего его пространства. Достаточно хорошим приближением поведения экситона является трехмерная модель частицы в ящике . Решение этой проблемы дает единственный математическая связь между энергетическими состояниями и размерностью пространства. Уменьшение объема или размеров доступного пространства увеличивает энергию состояний. На диаграмме показано изменение уровня энергии электронов и запрещенной зоны между наноматериалом и его объемным состоянием.

Следующее уравнение показывает взаимосвязь между уровнем энергии и расстоянием между измерениями:

$\psi _{n_{x},n_{y},n_{z}}={\sqrt {\frac {8}{L_{x}L_{y}L_{z}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{y}}}\right)\sin \left({\frac {n_{z}\pi z}{L_{z}}}\right)$

$E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2m}}\left[\left({\frac {n_{x}}{L_{x}}}\right)^{2}+\left({\frac {n_{y}}{L_{y}}}\right)^{2}+\left({\frac {n_{z}}{L_{z}}}\right)^{2}\right]$

Результаты исследования предоставить альтернативное объяснение изменения свойств на наноуровне. В объемной фазе поверхности, по-видимому, контролируют некоторые макроскопически наблюдаемые свойства. Однако в наночастицах поверхностные молекулы не подчиняются ожидаемой конфигурации. в космосе. В результате поверхностное натяжение сильно меняется.

Классическая механика

Классическое механическое объяснение использует закон Юнга – Лапласа, чтобы предоставить доказательства того, как падение давления увеличивается от масштаба к масштабу.

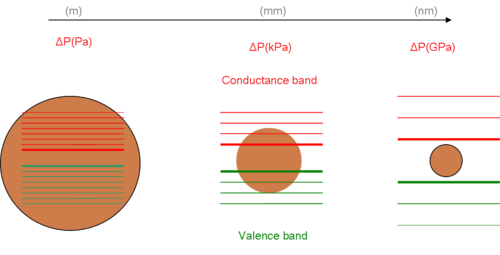
Уравнение Юнга-Лапласа может дать основу для исследования масштаба сил, приложенных к поверхностным молекулам:

${\begin{aligned}\Delta P&=\gamma \nabla \cdot {\hat {n}}\\&=2\gamma H\\&=\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)\end{aligned}}$

В предположении сферической формы $R_{1}=R_{2}=R$ и решая уравнение Юнга – Лапласа для новых радиусов $R$ (нм), оценим новую $\Delta P$(ГПа). Чем меньше радиусы, тем большее давление присутствует. Увеличение давления на наноуровне приводит к появлению сильных сил, направленных внутрь частицы. Следовательно, молекулярная структура частицы оказывается отличной от объемной, особенно на поверхности. Эти аномалии на поверхности ответственны за изменения межатомных взаимодействий и запрещенной зоны .

См. также

• Квантовая яма
• Конечная потенциальная яма
• Сколько вы даете?

Внешние ссылки

• Бухро В.Е., Колвин В.Л. (2003). «Полупроводниковые нанокристаллы: форма имеет значение». Нат Матер . 2 (3): 138–9. Бибкод : 2003NatMa...2..138B . дои : 10.1038/nmat844 . ПМИД   12612665 ​​. S2CID   13634895 .
• Основы полупроводников
• Ленточная теория твердого тела
• Синтез квантовых точек
• Биологическое применение