Дельта-сет

В математике Δ-множество , часто называемое Δ-комплексом или полусимплициальным множеством , представляет собой комбинаторный объект, который полезен при построении и триангуляции топологических пространств , а также при вычислении связанных алгебраических инвариантов таких пространств. Δ-множество является несколько более общим, чем симплициальный комплекс , но не столь сложным, как симплициальное множество . Симплициальные множества имеют дополнительную структуру, так что каждое симплициальное множество также является полусимплициальным множеством.

В качестве примера предположим, что мы хотим триангулировать одномерный круг. $S^{1}$ . Чтобы сделать это с симплициальным комплексом, нам нужны как минимум три вершины и ребра, соединяющие их. Но дельта-множества допускают более простую триангуляцию: думать о $S^{1}$ как интервал [0,1] с двумя идентифицированными конечными точками мы можем определить триангуляцию с одной вершиной 0 и одним ребром, проходящим между 0 и 0.

Определение и сопутствующие данные [ править ]

Формально ∆-множество — это последовательность множеств $\{S_{n}\}_{n=0}^{\infty }$ вместе с картами

d_{i}^{n}\colon S_{n+1}\rightarrow S_{n}

для каждого $n\geq 0$ и $i=0,1,\dots ,n+1$ , что удовлетворяет

d_{i}^{n}\circ d_{j}^{n+1}=d_{j-1}^{n}\circ d_{i}^{n+1}

в любое время $i<j$ . Часто верхний индекс ${d_{i}^{n}}$ опущено для краткости.

Это определение обобщает понятие симплициального комплекса, где $S_{n}$ являются наборами n -симплексов, а $d_{i}$ — это связанные карты лиц, каждая из которых отображает $i$ -я грань симплекса в $S_{n+1}$ к симплексу в $S_{n}$ . Правило композиции гарантирует, что лица в $S_{n+1}$ симплекса в $S_{n+2}$ поделиться своими соседскими лицами в $S_{n}$ , т. е. что симплексы корректны. Δ-множество не так общее, как симплициальное множество, поскольку в нем отсутствуют «вырождения».

Для данных Δ-множеств S и T карта Δ-множеств представляет собой набор отображений множеств.

\{f_{n}\colon S_{n}\rightarrow T_{n}\}_{n=0}^{\infty }

такой, что

f_{n}\circ d_{i}=d_{i}\circ f_{n+1}

всякий раз, когда определены обе части уравнения.

С помощью этого понятия мы можем определить категорию ∆-множеств , объекты которых являются ∆-множествами и чьи морфизмы являются отображениями ∆-множеств.

Каждое Δ-множество имеет соответствующую геометрическую реализацию , связывая геометрически определенное пространство (стандартный n-симплекс) с каждым абстрактным симплексом в Δ-множестве, а затем «склеивая» пространства вместе, используя отношения включения между пространствами для определения отношения эквивалентности. :

|S|=\left(\coprod _{n=0}^{\infty }S_{n}\times \Delta ^{n}\right)/_{\sim }

где мы заявляем ${\sim }$ как

(\sigma ,\iota ^{i}t)\sim (d_{i}\sigma ,t)\quad {\text{ for all }}\sigma \in S_{n},t\in \Delta ^{n-1}.

Здесь, $\Delta ^{n}$ обозначает стандартный n -симплекс как пространство, а

\iota ^{i}\colon \Delta ^{n-1}\rightarrow \Delta ^{n}

– включение i -й грани. Геометрическая реализация представляет собой топологическое пространство с фактортопологией .

Геометрическая реализация ∆-множества S имеет естественную фильтрацию

|S|_{0}\subset |S|_{1}\subset \cdots \subset |S|,

где

|S|_{N}=\left(\coprod _{n=0}^{N}S_{n}\times \Delta ^{n}\right)/_{\sim }

является «ограниченной» геометрической реализацией.

Связанные функторы [ править ]

Описанная выше геометрическая реализация ∆-множества определяет ковариантный функтор из категории ∆-множеств в категорию топологических пространств. Геометрическая реализация переводит Δ-множество в топологическое пространство и переносит отображения Δ-множеств в индуцированные непрерывные отображения между геометрическими реализациями.

Если S является Δ-множеством, существует связанный с ним свободный абелев цепной комплекс , обозначаемый $(\mathbb {Z} S,\partial )$ , n -я группа которого является свободной абелевой группой

(\mathbb {Z} S)_{n}=\mathbb {Z} \langle S_{n}\rangle ,

генерируется набором $S_{n}$ , и чей n -й дифференциал определяется формулой

\partial _{n}=d_{0}-d_{1}+d_{2}-\cdots +(-1)^{n}d_{n}.

Это определяет ковариантный функтор из категории ∆-множеств в категорию цепных комплексов абелевых групп. ∆-множество переносится в только что описанный цепной комплекс, а отображение ∆-множеств переносится в отображение цепных комплексов, которое определяется расширением отображения ∆-множеств стандартным способом с использованием универсального свойства свободных абелевы группы.

По любому топологическому пространству X можно построить ∆-множество $\mathrm {sing} (X)$ следующее. Особый n -симплекс в X — это непрерывное отображение

\sigma \colon \Delta ^{n}\rightarrow X.

Определять

\mathrm {sing} _{n}^{}(X)

быть совокупностью всех сингулярных n -простостей в X и определить

d_{i}\colon \mathrm {sing} _{i+1}(X)\rightarrow \mathrm {sing} _{i}(X)

к

d_{i}(\sigma )=\sigma \circ d^{i},

где снова $d^{i}$ это $i$ -я карта лица. Можно проверить, что это действительно ∆-множество. Это определяет ковариантный функтор из категории топологических пространств в категорию Δ-множеств. Топологическое пространство переносится в только что описанное Δ-множество, а непрерывное отображение пространств переносится в отображение Δ-множеств, которое задается составлением отображения с особыми n -симплексами.

Примеры [ править ]

Этот пример иллюстрирует описанные выше конструкции. Мы можем создать Δ-множество S , геометрической реализацией которого является единичный круг. $S^{1}$ и используйте его для вычисления гомологии этого пространства. Думать о $S^{1}$ как интервал с идентифицированными конечными точками, определим

S_{0}=\{v\},\quad S_{1}=\{e\},

с $S_{n}=\varnothing$ для всех $n\geq 2$ . Единственно возможные карты $d_{0},d_{1}\colon S_{1}\rightarrow S_{0},$ являются

d_{0}(e)=d_{1}(e)=v.\quad

Легко проверить, что это ∆-множество и что $|S|\cong S^{1}$ . Теперь связанный цепной комплекс $(\mathbb {Z} S,\partial )$ является

0\longrightarrow \mathbb {Z} \langle e\rangle {\stackrel {\partial _{1}}{\longrightarrow }}\mathbb {Z} \langle v\rangle \longrightarrow 0,

где

\partial _{1}(e)=d_{0}(e)-d_{1}(e)=v-v=0.

Фактически, $\partial _{n}=0$ для всех н . Гомологии этого цепного комплекса также легко вычислить:

H_{0}(\mathbb {Z} S)={\frac {\ker \partial _{0}}{\mathrm {im} \partial _{1}}}=\mathbb {Z} \langle v\rangle \cong \mathbb {Z} ,

H_{1}(\mathbb {Z} S)={\frac {\ker \partial _{1}}{\mathrm {im} \partial _{2}}}=\mathbb {Z} \langle e\rangle \cong \mathbb {Z} .

Все остальные группы гомологий, очевидно, тривиальны.

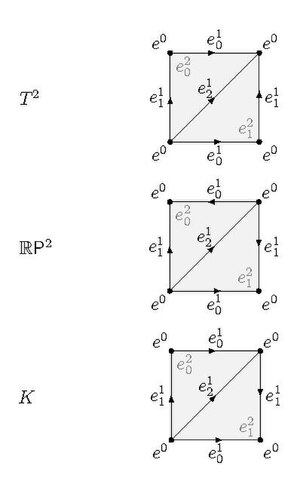
Следующий пример взят из раздела 2.1 « Алгебраической топологии Хэтчера». ^[1] Рассмотрим структуру Δ-множества, заданную тору на рисунке, который имеет одну вершину, три ребра и два 2-симплекса.

Карта границ $\partial _{1}$ равно 0, потому что существует только одна вершина, поэтому $H_{0}(T^{2})={\text{ker }}\partial _{0}/{\text{ im }}\partial _{1}=\mathbb {Z}$ . Позволять $\{e_{0}^{1},e_{1}^{1},e_{0}^{1}+e_{1}^{1}-e_{2}^{1}\}$ быть основой для $\Delta _{1}(T^{2})$ . Затем $\partial _{2}(e_{0}^{2})=e_{0}^{1}+e_{1}^{1}-e_{2}^{1}=\partial _{2}(e_{1}^{2})$ , так ${\text{im }}\partial _{2}=\langle e_{0}^{1}+e_{1}^{1}-e_{2}^{1}\rangle$ , и поэтому $H_{1}(T^{2})={\text{ker }}\partial _{1}/{\text{ im }}\partial _{2}=\mathbb {Z} ^{3}/\mathbb {Z} =\mathbb {Z} ^{2}.$

Поскольку 3-симплексов не существует, $H_{2}(T^{2})={\text{ker }}\partial _{2}$ . У нас есть это $\partial _{2}(pe_{0}^{2}+qe_{1}^{2})=(p+q)(e_{0}^{1}+e_{1}^{1}-e_{2}^{1})$ который равен 0 тогда и только тогда, когда $p=-q$ . Следовательно ${\text{ker }}\partial _{2}$ является бесконечной цикликой, порожденной $e_{0}^{2}-e_{1}^{2}$ .

Так $H_{2}(T^{2})=\mathbb {Z}$ . Четко $H_{n}(T^{2})=0$ для $n\geq 3.$

Таким образом, $H_{n}(T^{2})={\begin{cases}\mathbb {Z} &n=0,2\\\mathbb {Z} ^{2}&n=1\\0&n\geq 3.\end{cases}}$

Стоит подчеркнуть, что минимальное количество симплексов, необходимое для обеспечения $T^{2}$ со структурой симплициального комплекса составляет 7 вершин, 21 ребро и 14 2-симплексов, всего 42 симплекса. Это сделало бы приведенные выше расчеты, в которых использовалось только 6 симплексов, гораздо труднее выполнить вручную.

Это не пример. Рассмотрим отрезок прямой. Это одномерное Δ-множество и одномерное симплициальное множество. Однако если мы рассматриваем отрезок прямой как двумерное симплициальное множество, в котором 2-симплекс рассматривается как вырожденный, то отрезок прямой не является Δ-множеством, поскольку мы не допускаем таких вырождений.

Абстрактная чушь [ править ]

Теперь мы проверим связь между Δ-множествами и симплициальными множествами . Рассмотрим симплексную категорию $\Delta$ , объектами которого являются конечные вполне упорядоченные множества $[n]:=\{0,1,\cdots ,n\}$ и чьи морфизмы являются монотонными отображениями . Симплициальное множество определяется как предпучок на $\Delta$ , т.е. (контравариантная) функция $S:\Delta ^{\text{op}}\to {\text{Set}}$ . С другой стороны, рассмотрим подкатегорию ${\hat {\Delta }}$ из $\Delta$ морфизмы которого являются лишь строгими монотонными отображениями. Заметим, что морфизмы в ${\hat {\Delta }}$ именно инъекции в $\Delta$ , и можно доказать, что они порождены монотонными отображениями вида $\delta ^{i}:[n]\to [n+1]$ которые «пропускают» элемент $i\in [n+1]$ . Отсюда мы видим, что предпучок $S:{\hat {\Delta }}^{\text{op}}\to {\text{Set}}$ на ${\hat {\Delta }}$ определяется последовательностью множеств $\{S_{n}\}_{n=0}^{\infty }$ (где мы обозначаем $S([n])$ к $S_{n}$ для простоты) вместе с картами $d_{i}:S_{n+1}\to S_{n}$ для $i=0,1,\ldots ,n+1$ (где мы обозначаем $S(\delta ^{i})$ к $d_{i}$ для простоты тоже). Действительно, после проверки $\delta ^{j}\circ \delta ^{i}=\delta ^{i}\circ \delta ^{j-1}$ в ${\hat {\Delta }}$ , можно сделать вывод, что

d_{i}\circ d_{j}=d_{j-1}\circ d_{i}

в любое время $i<j$ . Таким образом, предпучок на ${\hat {\Delta }}$ определяет данные Δ-множества и, наоборот, все Δ-множества возникают таким образом. ^[2] Более того, ∆-отображения $f:S\to T$ между Δ-множествами соответствуют естественным преобразованиям , когда мы рассматриваем $S$ и $T$ как (контравариантные) функторы. В этом смысле Δ-множества являются предпучками на ${\hat {\Delta }}$ в то время как симплициальные множества являются предпучками на $\Delta$ .

С этой точки зрения теперь легко увидеть, что каждое симплициальное множество является Δ-множеством. Действительно, обратите внимание, что имеется включение ${\hat {\Delta }}\hookrightarrow \Delta$ ; так что каждое симплициальное множество $S:\Delta ^{\text{op}}\to {\text{Set}}$ естественным образом порождает Δ-множество, а именно составное ${\textstyle {\hat {\Delta }}^{\text{op}}\hookrightarrow \Delta ^{\text{op}}\xrightarrow {S} {\text{Set}}}$ .

Плюсы и минусы [ править ]

Одним из преимуществ использования Δ-множеств таким способом является то, что полученный цепной комплекс обычно намного проще, чем сингулярный цепной комплекс . Для достаточно простых пространств все группы будут конечно порождены, тогда как группы сингулярных цепей, как правило, даже не счетно порождены.

Недостатком этого метода является необходимость доказать, что геометрическая реализация Δ-множества на самом деле гомеоморфна рассматриваемому топологическому пространству. Это может стать вычислительной проблемой, поскольку сложность Δ-множества увеличивается.

См. также [ править ]

Ссылки [ править ]

^ Хэтчер, Аллен (2002). Алгебраическая топология . Кембридж: Издательство Кембриджского университета. ISBN 0-521-79160-Х . OCLC 45420394 .
^ Фридман, Грег (2012). «Обзорная статья: элементарное иллюстрированное введение в симплициальные множества». Математический журнал Роки Маунтин . 42 (2): 353–423. arXiv : 0809.4221 . дои : 10.1216/RMJ-2012-42-2-353 . МР 2915498 .

Раницки, Эндрю А. (1993). Алгебраическая L-теория и топологические многообразия (PDF) . Кембриджские трактаты по математике. Том. 102. Кембриджский университет. Нажимать . ISBN 978-0-521-42024-2 .
Раницки, Эндрю ; Вайс, Майкл (2012). «Об алгебраической L-теории Δ-множеств». Ежеквартальный журнал «Чистая и прикладная математика» . 8 (2): 423–450. arXiv : math.AT/0701833 . дои : 10.4310/pamq.2012.v8.n2.a3 . МР 2900173 .
Рурк, Колин П .; Сандерсон, Брайан Дж. (1971). «Δ-множества I: теория гомотопии». Ежеквартальный математический журнал . 22 (3): 321–338. Бибкод : 1971QJMat..22..321R . дои : 10.1093/qmath/22.3.321 .

[1] Хэтчер, Аллен (2002). Алгебраическая топология . Кембридж: Издательство Кембриджского университета. ISBN 0-521-79160-Х . OCLC 45420394 .

[2] Фридман, Грег (2012). «Обзорная статья: элементарное иллюстрированное введение в симплициальные множества». Математический журнал Роки Маунтин . 42 (2): 353–423. arXiv : 0809.4221 . дои : 10.1216/RMJ-2012-42-2-353 . МР 2915498 .

[1]

[2]