Байесовская модель вычислительной анатомии

Дополнительная информация: Диффеоморфное метрическое отображение большой деформации и байесовская оценка шаблонов в вычислительной анатомии.

Основная статья: Вычислительная анатомия

Вычислительная анатомия (КА) — это дисциплина в области медицинской визуализации, фокусирующаяся на изучении анатомической формы и формы на видимом или грубом анатомическом уровне морфологии . Эта область имеет широкое определение и включает в себя основы анатомии , прикладной математики и чистой математики , включая медицинскую визуализацию , нейробиологию , физику , теорию вероятностей и статистику . Основное внимание уделяется визуализируемым анатомическим структурам, а не медицинским устройствам визуализации. Центральным направлением области компьютерной анатомии в медицинской визуализации является отображение информации в анатомических системах координат, чаще всего плотная информация, измеряемая с помощью магнитно-резонансного изображения (МРТ). Введение потоков в CA, которые похожи на уравнения движения, используемые в гидродинамике, используют представление о том, что плотные координаты при анализе изображений следуют Лагранжа и Эйлера уравнениям движения . В моделях, основанных на лагранжевых и эйлеровых потоках диффеоморфизмов, ограничение связано с топологическими свойствами, такими как сохранение открытых множеств, непересечение координат, что подразумевает уникальность и существование обратного отображения, а также связные множества, остающиеся связанными. Использование диффеоморфных методов быстро стало доминировать в области методов картографии после работы Кристенсена. оригинальная статья, в которой становятся доступными быстрые и симметричные методы.

Основная статистическая модель

Модель исходного канала, показывающая источник изображений - деформируемый шаблон. $I\doteq \varphi \cdot I_{\mathrm {temp} }\in {\mathcal {I}}$ и выходной канал, связанный с датчиком МРТ $I^{D}\in {\mathcal {I}}^{\mathcal {D}}$

Центральной статистической моделью вычислительной анатомии в контексте медицинской визуализации была модель источника-канала теории Шеннона ; источник — деформируемый шаблон изображений $I\in {\mathcal {I}}$выходы канала представляют собой датчики изображения с наблюдаемыми $I^{D}\in {\mathcal {I}}^{\mathcal {D}}$ (см. рисунок). Важность модели исходного канала заключается в том, что вариации анатомической конфигурации моделируются отдельно от вариаций датчиков медицинских изображений. гласит Теория Байеса , что модель характеризуется априорным значением источника: $\pi _{\mathcal {I}}(\cdot )$ на $I\in {\mathcal {I}}$, а условная плотность на наблюдаемой

$p(\cdot \mid I){\text{ on }}I^{D}\in {\mathcal {I}}^{\mathcal {D}}$

обусловлено $I\in {\mathcal {I}}$.

В теории деформируемых шаблонов изображения связаны с шаблонами, причем деформации представляют собой группу, которая действует на шаблон;см. групповое действие в вычислительной анатомии. Для имиджевого действия $I(g)\doteq g\cdot I_{\mathrm {temp} },g\in {\mathcal {G}}$, то априор группы $\pi _{\mathcal {G}}(\cdot )$ вызывает априор на изображениях $\pi _{\mathcal {I}}(\cdot )$, записанная как плотности, логарифмическая апостериорная принимает форму

$\log p(I(g)\mid I^{D})\simeq \log p(I^{D}\mid I(g))+\log \pi _{\mathcal {G}}(g).$

Следующая модель случайной орбиты определяет, как генерировать элементы группы и, следовательно, случайный разброс объектов, которые формируют априорное распределение.

Модель случайной орбиты вычислительной анатомии

Орбиты мозга, связанные с действием диффеоморфной группы на шаблоны, изображенные посредством плавного потока, связанного с геодезическими потоками со случайным распылением, связанным со случайной генерацией начального векторного поля касательного пространства. $v_{0}\in V$; опубликовано в.

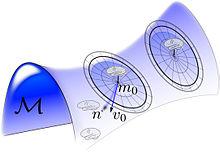
Модель случайной орбиты вычислительной анатомии впервые появилась в моделирование изменения координат, связанное со случайностью группы, воздействующей на шаблоны, что наводит случайность на источник изображения в анатомической орбите форм и форм и приводит к наблюдениям через устройства медицинской визуализации. Такая модель случайной орбиты , в которой случайность в группе вызывает случайность в изображениях, была исследована для Специальной евклидовой группы распознавания объектов, в которой элемент группы $g\in {\mathcal {G}}$ была особая евклидова группа.

Для изучения деформируемой формы в СА многомерные группы диффеоморфизмов, используемые в вычислительной анатомии, генерируются с помощью гладких потоков. $\varphi _{t},t\in [0,1]$ которые удовлетворяют лагранжевой и эйлеровой спецификации полей потока, удовлетворяющих обыкновенному дифференциальному уравнению:

Показ лагранжева потока координат $x\in X$ со связанными векторными полями $v_{t},t\in [0,1]$ удовлетворяющее обыкновенному дифференциальному уравнению ${\dot {\varphi }}_{t}=v_{t}(\varphi _{t}),\varphi _{0}=id$.

${\frac {d}{dt}}\varphi _{t}=v_{t}\circ \varphi _{t},\ \varphi _{0}=\operatorname {id} \ ;$ ( Лагранжев поток )

с $v\doteq (v_{1},v_{2},v_{3})$ векторные поля на ${\mathbb {R} }^{3}$ называется эйлеровой скоростью частиц в положении $\varphi$ потока. Векторные поля представляют собой функции в функциональном пространстве, смоделированном как гладкое гильбертово пространство с векторными полями, имеющими 1-непрерывную производную. Для $v_{t}={\dot {\varphi }}_{t}\circ \varphi _{t}^{-1},t\in [0,1]$, обратный поток определяется выражением

${\frac {d}{dt}}\varphi _{t}^{-1}=-(D\varphi _{t}^{-1})v_{t},\ \varphi _{0}^{-1}=\operatorname {id} ,$ ( Эйлеров поток )

и $3\times 3$ Матрица Якоби для потоков в $\mathbb {R} ^{3}$ дано как $\ D\varphi \doteq \left({\frac {\partial \varphi _{i}}{\partial x_{j}}}\right).$

Для обеспечения гладкости потоков диффеоморфизмов с обратными векторные поля ${\mathbb {R} }^{3}$ должна быть хотя бы 1-кратно непрерывно дифференцируема в пространстве которые моделируются как элементы гильбертова пространства $(V,\|\cdot \|_{V})$ используя теоремы вложения Соболева так, чтобы каждый элемент $v_{i}\in H_{0}^{3},i=1,2,3,$ имеет производные, интегрируемые с 3 квадратами. Таким образом $(V,\|\cdot \|_{V})$ плавно вкладываются в 1-раз непрерывно дифференцируемые функции. Группа диффеоморфизмов — это потоки с векторными полями, абсолютно интегрируемыми в соболевской норме:

$\operatorname {Diff} _{V}\doteq \left\{\varphi =\varphi _{1}:{\dot {\varphi }}_{t}=v_{t}\circ \varphi _{t},\varphi _{0}=\operatorname {id} ,\int _{0}^{1}\|v_{t}\|_{V}\,dt<\infty \right\},$ ( группа диффеоморфизмов )

где $\|v_{t}\|_{V}^{2}\doteq \int _{X}Av_{t}\cdot v_{t}dx$ с $A$ линейный оператор $A:V\mapsto V^{*}$ определяющие норму РХС. Интеграл вычисляется интегрированием по частям, когда $Av$ является обобщенной функцией в дуальном пространстве $V^{*}$.

Риманова экспонента

Дополнительная информация: Риманова метрика и скобки Ли в вычислительной анатомии.

В модели случайной орбиты вычислительной анатомии весь поток сводится к начальному состоянию, которое формирует координаты, кодирующие диффеоморфизм. Из начального состояния $v_{0}$ тогда геодезическое позиционирование относительно римановой метрики вычислительной анатомии решает поток уравнения Эйлера-Лагранжа.Решение геодезической из начального условия $v_{0}$ называется римановой экспонентой, отображением $\operatorname {Exp} _{\mathrm {id} }(\cdot ):V\to \operatorname {Diff} _{V}$ при принадлежности к группе.

Риманова экспонента удовлетворяет $\operatorname {Exp} _{\mathrm {id} }(v_{0})=\varphi _{1}$ для исходного состояния ${\dot {\varphi }}_{0}=v_{0}$, динамика векторного поля ${\dot {\varphi }}_{t}=v_{t}\circ \varphi _{t},t\in [0,1]$,

• для классического уравнения диффеоморфной формы импульс $\int _{X}Av_{t}\cdot w\,dx$, $Av\in V$, затем

${\frac {d}{dt}}Av_{t}+(Dv_{t})^{T}Av_{t}+(DAv_{t})v_{t}+(\nabla \cdot v)Av_{t}=0\ ;$

• для обобщенного уравнения, то $Av\in V^{*}$, $w\in V$

$\int _{X}{\frac {d}{dt}}Av_{t}\cdot w\,dx+\int _{X}Av_{t}\cdot ((Dv_{t})w-(Dw)v_{t})\,dx=0.$

Распространяется на всю группу, $\varphi =\operatorname {Exp} _{\varphi }(v_{0}\circ \varphi )\doteq \operatorname {Exp} _{\mathrm {id} }(v_{0})\circ \varphi .$На прилагаемом рисунке изображены случайные орбиты вокруг каждого образца. $m_{0}\in {\mathcal {M}}$, сгенерированный путем рандомизации потока путем генерации начального векторного поля касательного пространства в тождестве $v_{0}\in V$, а затем генерируем случайный объект $n\doteq \operatorname {Exp} _{\mathrm {id} }(v_{0})\cdot m_{0}\in {\mathcal {M}}$.

На рисунке показано случайное распыление синтезированных подкорковых структур, расположенных в двумерной сетке, представляющей дисперсию собственной функции, используемой для определения импульса для синтеза.

На рисунке справа показана мультяшная орбита, представляющая собой случайный спрей подкорковых многообразий, созданный путем рандомизации векторных полей. $v_{0}$ поддерживается над подмногообразиями. Модель случайной орбиты индуцирует априорное отношение к формам и изображениям. $I\in {\mathcal {I}}$ обусловленный определенным атласом $I_{a}\in {\mathcal {I}}$. Для этого генеративная модель генерирует среднее поле $I$ как случайное изменение координат шаблона по $I\doteq \varphi \cdot I_{a}$, где диффеоморфное изменение координат генерируется случайным образом посредством геодезических потоков.

Оценка MAP в модели орбиты с несколькими атласами

Модель случайной орбиты индуцирует априорные формы и изображения. $I\in {\mathcal {I}}$ обусловленный определенным атласом $I_{a}\in {\mathcal {I}}$. Для этого генеративная модель генерирует среднее поле $I$ как случайное изменение координат шаблона по $I\doteq \varphi \cdot I_{a}$, где диффеоморфное изменение координат генерируется случайным образом посредством геодезических потоков. Априор о случайных преобразованиях $\pi _{\mathrm {Diff} }(d\varphi )$ на $\operatorname {Diff} _{V}$ индуцируется потоком $\operatorname {Exp} _{\mathrm {id} }(v)$, с $v\in V$ построенное как гауссово случайное поле до $\pi _{V}(dv)$. Плотность случайных наблюдаемых на выходе датчика $I^{D}\in {\mathcal {I}}^{D}$ даны

$p(I^{D}\mid I_{a})=\int _{V}p(I^{D}\mid \operatorname {Exp} _{\mathrm {id} }(v)\cdot I_{a})\pi _{V}(dv)\ .$

Оценка максимальной апостериорной оценки (MAP) занимает центральное место в современной статистической теории . Интересующие параметры $\theta \in \Theta$ принимать множество форм, включая (i) тип заболевания, такой как нейродегенеративные заболевания или заболевания , связанные с развитием нервной системы , (ii) тип структуры, такой как корковые или подкорковые структуры, при проблемах, связанных с сегментацией изображений, и (iii) реконструкцию шаблонов из популяций. Учитывая наблюдаемое изображение $I^{D}$, оценка MAP максимизирует апостериорную величину:

${\hat {\theta }}\doteq \arg \max _{\theta \in \Theta }\log p(\theta \mid I^{D}).$

Для этого необходимо вычислить условные вероятности $p(\theta \mid I^{D})={\frac {p(I^{D},\theta )}{p(I^{D})}}$. Модель множественных орбит атласа рандомизирует счетный набор атласов. $\{I_{a},a\in {\mathcal {A}}\}$. Модель изображений на орбите имеет вид распределения мультимодальной смеси.

$p(I^{D},\theta )=\sum _{a\in {\mathcal {A}}}p(I^{D},\theta \mid I_{a})\pi _{\mathcal {A}}(a)\ .$

Условная модель Гаусса тщательно исследовалась на предмет неточного сопоставления на плотных изображениях и сопоставления ориентиров.

Плотное сопоставление изображений

Модель $I^{D}(x),x\in X$ как условно гауссово случайное поле, обусловленное средним полем, $\varphi _{1}\cdot I\doteq I(\varphi _{1}^{-1}),\varphi _{1}\in Diff_{V}$. Для равномерной дисперсии члены ошибки конечной точки играют роль логарифмического условия (только функции среднего поля), определяющего термин конечной точки:

$-\log p(I^{D}\mid I(g))\simeq E(\varphi _{1})\doteq {\frac {1}{2\sigma ^{2}}}\|I^{D}-I\circ \varphi _{1}^{-1}\|^{2}.$

( Условно-гауссово )

Сопоставление ориентиров

Модель $Y=\{y_{1},y_{2},\dots \}$ как условно гауссово со средним полем $\varphi _{1}(x_{i}),i=1,2,\dots ,\varphi _{1}\in \operatorname {Diff} _{V}$, постоянная дисперсия шума, не зависящая от ориентиров. Лог-условие (только функция среднего поля) можно рассматривать как термин конечной точки:

$-\log p(I^{D}\mid I(g))\simeq \operatorname {E} (\varphi _{1})\doteq {\frac {1}{2\sigma ^{2}}}\sum _{i}\|y_{i}-\varphi _{1}(x_{i})\|^{2}.$

Сегментация MAP на основе нескольких атласов

Модель случайной орбиты для нескольких атласов моделирует орбиту форм как объединение нескольких анатомических орбит, возникающих в результате группового действия диффеоморфизмов. ${\mathcal {I}}=\textstyle \bigcup _{a\in {\mathcal {A}}}\displaystyle \operatorname {Diff} _{V}\cdot I_{a}$, при этом каждый атлас имеет шаблон и предопределенное поле сегментации. $(I_{a},W_{a}),a=a_{1},a_{2},\ldots$. включение парцелляции в анатомические структуры координаты МРТ. Пары индексируются по решетке вокселей. $I_{a}(x_{i}),W_{a}(x_{i}),x_{i}\in X\subset {\mathbb {R} }^{3}$ с изображением МРТ и плотной маркировкой каждой координаты вокселя. Анатомическая маркировка парцеллированных структур проводится нейроанатомами вручную.

Проблема сегментации Байеса дано измерение $I^{D}$ со средним полем и парцелляцией $(I,W)$, анатомическая маркировка $\theta \doteq W$. необходимо оценивать для измеренного МРТ-изображения. Среднее поле наблюдаемой $I^{D}$ изображение моделируется как случайная деформация одного из шаблонов $I\doteq \varphi \cdot I_{a}$, который также выбирается случайным образом, $A=a$,. Оптимальный диффеоморфизм $\varphi \in {\mathcal {G}}$ скрыт и действует на фоновом пространстве координат случайно выбранного изображения-шаблона $I_{a}$. Учитывая один атлас $a$, модель правдоподобия для вывода определяется совместной вероятностью $p(I^{D},W\mid A=a)$; при использовании нескольких атласов объединение функций правдоподобия дает модель мультимодальной смеси с предварительным усреднением по моделям.

Оценщик сегментации MAP $W_{a}$ это максимизатор $\max _{W}\log p(W\mid I^{D})$ данный $I^{D}$, что включает в себя смесь по всем атласам.

${\hat {W}}\doteq \arg \textstyle \max _{W}\displaystyle \log p(I^{D},W){\text{ with }}p(I^{D},W)=\textstyle \sum _{a\in {\mathcal {A}}}\displaystyle p(I^{D},W\mid A=a)\pi _{A}(a).$

Количество $p(I^{D},W)$ вычисляется путем слияния вероятностей из нескольких деформируемых атласов с $\pi _{A}(a)$ априорная вероятность того, что наблюдаемое изображение развивается из конкретного шаблонного изображения. $I_{a}$.

Сегментация MAP может быть решена итеративно с помощью алгоритма ожидания-максимизации.

$W^{\text{new}}\doteq \arg \max _{W}\int \log p(W,I^{D},A,\varphi )\,dp(A,\varphi \mid W^{\text{old}},I^{D}).$

Оценка MAP шаблонов объема по популяциям и алгоритм EM

Эмпирическое создание шаблонов на основе совокупностей является фундаментальной операцией, повсеместно используемой в этой дисциплине.Для подмногообразий и плотных объемов изображений появилось несколько методов, основанных на байесовской статистике.Для случая плотного объема изображения, учитывая наблюдаемую $I^{D_{1}},I^{D_{2}},\dots$ проблема в том, чтобы оценить шаблон на орбите плотных изображений $I\in {\mathcal {I}}$. Процедура Ма использует исходный гипершаблон. $I_{0}\in {\mathcal {I}}$ в качестве отправной точки и моделирует шаблон на орбите при неизвестном, подлежащем оценке диффеоморфизме $I\doteq \varphi _{0}\cdot I_{0}$, с параметрами, подлежащими оценке, лог-координатами $\theta \doteq v_{0}$ определение геодезического отображения гипершаблона $\operatorname {Exp} _{\mathrm {id} }(v_{0})\cdot I_{0}=I\in {\mathcal {I}}$.

В байесовской модели случайной орбиты вычислительной анатомии наблюдаемые МРТ-изображения $I^{D_{i}}$ моделируются как условно гауссово случайное поле со средним полем $\varphi _{i}\cdot I$, с $\varphi _{i}$ случайное неизвестное преобразование шаблона. Проблема оценки MAP состоит в том, чтобы оценить неизвестный шаблон. $I\in {\mathcal {I}}$ учитывая наблюдаемые изображения МРТ.

Процедура Ма для плотных изображений использует исходный гипершаблон. $I_{0}\in {\mathcal {I}}$ в качестве отправной точки и моделирует шаблон на орбите при неизвестном, подлежащем оценке диффеоморфизме $I\doteq \varphi _{0}\cdot I_{0}$. Наблюдаемые моделируются как условные случайные поля, $I^{D_{i}}$ условно -гауссово случайное поле со средним полем $\varphi _{i}\cdot I\doteq \varphi _{i}\cdot \varphi _{0}\cdot I_{0}$. Неизвестная переменная, которую необходимо явно оценить с помощью MAP, представляет собой отображение гипершаблона. $\varphi _{0}$, а другие отображения рассматриваются как мешающие или скрытые переменные, которые интегрируются с помощью процедуры Байеса. Это достигается с помощью алгоритма ожидания-максимизации .

Орбитальная модель используется путем привязки неизвестных оцениваемых потоков к их логарифмическим координатам. $v_{i},i=1,\dots$ через риманов геодезический журнал и экспоненту для вычислительной анатомии начальное векторное поле в касательном пространстве в единице, так что $\operatorname {Exp} _{\mathrm {id} }(v_{i})\doteq \varphi _{i}$, с $\operatorname {Exp} _{\mathrm {id} }(v_{0})$ отображение гипершаблона.Проблема оценки MAP становится

$\max _{v_{0}}p(I^{D},\theta =v_{0})=\int p(I^{D},\theta =v_{0}\mid v_{1},v_{2},\dots )\pi (v_{1},v_{2},\dots )\,dv$

Алгоритм EM принимает в качестве полных данных координаты векторного поля, параметризующие отображение, $v_{i},i=1,\dots$ и итеративно вычисляем условное ожидание

${\begin{cases}Q(\theta =v_{0};\theta ^{\text{old}}=v_{0}^{\text{old}})&=-\operatorname {E} (\log p(I^{D},\theta =v_{0}\mid v_{1},v_{2},\dots )\mid I^{D},\theta ^{\text{old}})\\&=-\|({\bar {I}}^{\text{old}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0})^{-1}){\sqrt {\beta ^{\text{old}}}}\|^{2}-\|v_{0}\|_{V}^{2}\end{cases}}$

• Вычислить новый шаблон, максимизирующий Q-функцию, установив

$\theta ^{\text{new}}\doteq v_{0}^{\text{new}}=\arg \max _{\theta =v_{0}}Q(\theta ;\theta ^{\text{old}}=v_{0}^{\text{old}})=-\left\|({\bar {I}}^{\text{old}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0})^{-1}){\sqrt {\beta ^{\text{old}}}}\right\|^{2}-\|v_{0}\|_{V}^{2}$

• Вычислите аппроксимацию режима для ожидания, обновляющего ожидаемые значения для значений режима:

$v_{i}^{\text{new}}=\arg \max _{v:{\dot {\varphi }}=v\circ \varphi }-\int _{0}^{1}\|v_{t}\|_{V}^{2}\,dt-\|I^{D_{i}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0}^{\text{old}})^{-1}\circ \operatorname {Exp} _{\mathrm {id} }(v)^{-1}\|^{2}.i=1,2,\dots$

$\beta ^{\text{new}}(x)=\sum _{i=1}^{n}|D\operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})(x)|,{\text{ with }}{\bar {I}}^{\text{new}}(x)={\frac {\sum _{i=1}^{n}I^{D_{i}}\circ \operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})|D\operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})(x)|}{\beta ^{\text{old}}(x)}}$