Соленоид

Эта статья о электромагните. Чтобы узнать об устройстве, преобразующем электричество в механическую энергию, см. соленоид (техника) . Чтобы узнать о других значениях, см. Соленоид (значения) .

Иллюстрация соленоида

Магнитное поле, создаваемое семиконтурным соленоидом (вид в разрезе), описываемое с помощью силовых линий.

Демонстрация магнитного поля с помощью изолированного провода соленоидной формы и железных опилок

Соленоид ​ ( / ˈ s oʊ l ə n ɔɪ d / ) — тип электромагнита, образованный спиральной катушкой из проволоки , длина которой существенно превышает ее диаметр, который генерирует управляемое магнитное поле . Катушка может создавать однородное магнитное поле в объеме пространства при электрического тока пропускании через нее .

Андре-Мари Ампер ввел термин «соленоид» в 1823 году, задумав устройство в 1820 году. Французский термин, первоначально созданный Ампером, — Solénoide , который является французской транслитерацией греческого слова σωληνοειδὴς , что означает трубчатый .

Винтовая катушка соленоида не обязательно должна вращаться вокруг прямой оси; например, электромагнит Уильяма Стерджена 1824 года состоял из соленоида, изогнутого в форме подковы (аналогично дуговой пружине ).

Соленоиды обеспечивают магнитную фокусировку электронов в вакууме, особенно в трубках телевизионных камер, таких как видиконы и ортиконы изображений. Электроны двигаются по спиральным траекториям внутри магнитного поля. Эти соленоиды, катушки фокусировки, окружают трубку почти по всей длине.

Физика

Бесконечный непрерывный соленоид

Рисунок 1: Бесконечный соленоид с тремя произвольными петлями Ампера, обозначенными a , b и c . Интегрирование по пути c показывает, что магнитное поле внутри соленоида должно быть однородным в радиальном направлении.

Бесконечный соленоид имеет бесконечную длину, но конечный диаметр. «Непрерывный» означает, что соленоид состоит не из отдельных катушек конечной ширины, а из множества бесконечно тонких катушек без пространства между ними; в этой абстракции соленоид часто рассматривается как цилиндрический лист проводящего материала.

Магнитное поле внутри бесконечно длинного соленоида однородно и его напряженность не зависит ни от расстояния от оси, ни от площади поперечного сечения соленоида.

Это расчет плотности магнитного потока вокруг соленоида, который достаточно длинный, чтобы можно было игнорировать краевые эффекты. На рисунке 1 мы сразу знаем, что вектор плотности потока указывает в положительном направлении z внутри соленоида и в отрицательном направлении z снаружи соленоида. Мы подтверждаем это, применяя правило правой руки к полю вокруг провода. Если мы обхватим провод правой рукой так, чтобы большой палец был направлен в направлении тока, то сгибание пальцев покажет, как ведет себя поле. Поскольку мы имеем дело с длинным соленоидом, все компоненты магнитного поля, не направленные вверх, уравновешиваются симметрией. Снаружи происходит аналогичная отмена, и поле направлено только вниз.

Теперь рассмотрим воображаемую петлю c , расположенную внутри соленоида. По закону Ампера мы знаем, что линейный интеграл от B (вектора плотности магнитного потока) вокруг этой петли равен нулю, поскольку в ней нет электрических токов (можно также предположить, что электрическое поле цепи, проходящее через петлю, постоянно при такой петле). условия: постоянный или постоянно меняющийся ток через соленоид). Выше мы показали, что поле внутри соленоида направлено вверх, поэтому горизонтальные части контура c не вносят никакого вклада в интеграл. Таким образом, интеграл от верхней стороны 1 равен интегралу от нижней стороны 2. Поскольку мы можем произвольно изменять размеры петли и получать тот же результат, единственное физическое объяснение состоит в том, что подынтегральные выражения на самом деле равны, то есть Магнитное поле внутри соленоида радиально однородно. Заметим, однако, что ничто не запрещает ей изменяться в продольном направлении, что, собственно, и происходит.

Аналогичный аргумент можно применить к петле a, чтобы заключить, что поле вне соленоида радиально однородно или постоянно. Этот последний результат, который строго верен только вблизи центра соленоида, где силовые линии параллельны его длине, важен, поскольку показывает, что плотность потока снаружи практически равна нулю, поскольку радиусы поля вне соленоида будут стремиться к бесконечность. Интуитивный аргумент также можно использовать, чтобы показать, что плотность потока вне соленоида на самом деле равна нулю. Линии магнитного поля существуют только в виде петель, они не могут расходиться или сходиться к точке, как это могут делать линии электрического поля (см. Закон Гаусса для магнетизма ). Линии магнитного поля следуют продольному пути соленоида внутри, поэтому они должны идти в противоположном направлении снаружи соленоида, чтобы линии могли образовывать петли. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий магнитного поля снаружи значительно уменьшается. Теперь вспомним, что поле снаружи постоянно. Чтобы общее количество силовых линий сохранялось, внешнее поле должно стремиться к нулю по мере увеличения длины соленоида. Конечно, если соленоид выполнен в виде проволочной спирали (как это часто делается на практике), то он излучает внешнее поле так же, как и одиночный провод, из-за тока, протекающего по всей длине соленоида.

Как закон Ампера можно применить к соленоиду

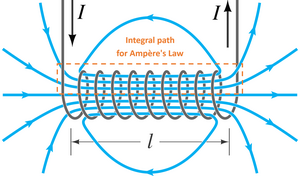
Применение закона цепи Ампера к соленоиду (см. рисунок справа) дает нам

$Bl=\mu _{0}NI,$

где $B$ – плотность магнитного потока , $l$ длина соленоида, $\mu _{0}$ магнитная постоянная , $N$ количество витков и $I$ электрический ток. Из этого мы получаем

$B=\mu _{0}{\frac {NI}{l}}.$

Это уравнение справедливо для соленоида в свободном пространстве, а это означает, что проницаемость магнитного пути такая же, как и проницаемость свободного пространства, µ ₀ .

Если соленоид погружен в материал с относительной проницаемостью µ _r , то поле увеличивается на эту величину:

$B=\mu _{0}\mu _{\mathrm {r} }{\frac {NI}{l}}.$

В большинстве соленоидов соленоид не погружен в материал с более высокой проницаемостью, а скорее некоторая часть пространства вокруг соленоида имеет материал с более высокой проницаемостью, а часть представляет собой просто воздух (который ведет себя во многом как свободное пространство). В этом сценарии полный эффект от материала с высокой проницаемостью не виден, но будет эффективная (или кажущаяся) проницаемость μ _eff такая, что 1 ≤ μ _eff ≤ μ _r .

Включение ферромагнитного сердечника, например железа , увеличивает величину плотности магнитного потока в соленоиде и повышает эффективную проницаемость магнитного пути. Это выражается формулой

$B=\mu _{0}\mu _{\mathrm {eff} }{\frac {NI}{l}}=\mu {\frac {NI}{l}},$

где μ _эфф — эффективная или кажущаяся проницаемость керна. Эффективная проницаемость является функцией геометрических свойств керна и его относительной проницаемости. Термины относительная проницаемость (свойство только материала) и эффективная проницаемость (свойство всей конструкции) часто путают; они могут отличаться на многие порядки.

Для открытой магнитной структуры связь между эффективной и относительной проницаемостью определяется следующим образом:

$\mu _{\mathrm {eff} }={\frac {\mu _{r}}{1+k(\mu _{r}-1)}},$

где k – коэффициент размагничивания сердечника.

Конечный непрерывный соленоид

Конечный соленоид — это соленоид конечной длины. Непрерывный означает, что соленоид состоит не из отдельных катушек, а из листа проводящего материала. Предположим, что ток равномерно распределен по поверхности соленоида с поверхностной плотностью тока K ; в цилиндрических координатах : $${\vec {K}}={\frac {I}{l}}{\hat {\phi }}.$$

Магнитное поле можно найти с помощью векторного потенциала , который для конечного соленоида радиусом R и длиной l в цилиндрических координатах $(\rho ,\phi ,z)$ является $$A_{\phi }={\frac {\mu _{0}I}{\pi }}{\frac {R}{l}}\left[{\frac {\zeta }{\sqrt {(R+\rho )^{2}+\zeta ^{2}}}}\left({\frac {m+n-mn}{mn}}K(m)-{\frac {1}{m}}E(m)+{\frac {n-1}{n}}\Pi (n,m)\right)\right]_{\zeta _{-}}^{\zeta _{+}},$$

Линии магнитного поля и плотность, создаваемые соленоидом с поверхностной плотностью тока

Где:

• $\zeta _{\pm }=z\pm {\frac {l}{2}}$,
• $n={\frac {4R\rho }{(R+\rho )^{2}}}$,
• $m={\frac {4R\rho }{(R+\rho )^{2}+\zeta ^{2}}}$,
• $K(m)=\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\sqrt {1-m\sin ^{2}\theta }}}$,
• $E(m)=\int _{0}^{\frac {\pi }{2}}{\sqrt {1-m\sin ^{2}\theta }}\,d\theta$ ,
• $\Pi (n,m)=\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{(1-n\sin ^{2}\theta ){\sqrt {1-m\sin ^{2}\theta }}}}$ .

Здесь, $K(m)$, $E(m)$, и $\Pi (n,m)$ являются полными эллиптическими интегралами первого, второго и третьего рода.

С использованием:

$${\vec {B}}=\nabla \times {\vec {A}},$$

Плотность магнитного потока получается как $$B_{\rho }={\frac {\mu _{0}I}{4\pi }}{\frac {1}{l\,\rho }}\left[{\sqrt {(R+\rho )^{2}+\zeta ^{2}}}{\biggl (}(m-2)K(m)+2E(m){\biggr )}\right]_{\zeta _{-}}^{\zeta _{+}},$$ $$B_{z}={\frac {\mu _{0}I}{2\pi }}{\frac {1}{l}}\left[{\frac {\zeta }{\sqrt {(R+\rho )^{2}+\zeta ^{2}}}}\left(K(m)+{\frac {R-\rho }{R+\rho }}\Pi (n,m)\right)\right]_{\zeta _{-}}^{\zeta _{+}}.$$

На оси симметрии радиальная компонента исчезает, а аксиальная компонента поля равна $$B_{z}={\frac {\mu _{0}NI}{2}}\left({\frac {l/2-z}{l{\sqrt {R^{2}+(l/2-z)^{2}}}}}+{\frac {l/2+z}{l{\sqrt {R^{2}+(l/2+z)^{2}}}}}\right).$$ Внутри соленоида, далеко от торцов ( $l/2-|z|\gg R$), это стремится к постоянному значению $B=\mu _{0}NI/l$.

Краткая оценка соленоида

Для случая, когда радиус много больше длины соленоида ( $R\gg l$), плотность магнитного потока через центр соленоида (в направлении z , параллельно длине соленоида, где центр катушки находится в точке z =0) можно оценить как плотность потока одиночной круглой проводниковой петли:

$B_{z}\approx {\frac {\mu _{0}INR^{2}}{2{\sqrt {R^{2}+z^{2}}}^{3}}}$

Нерегулярные соленоиды

Примеры соленоидов неправильной формы (а) разреженный соленоид, (б) соленоид с переменным шагом, (в) нецилиндрический соленоид

В категорию конечных соленоидов входят те, которые имеют редкую намотку с одним шагом, те, которые имеют редкую намотку с разным шагом (соленоиды с переменным шагом), и те, которые имеют разные радиусы для разных контуров (нецилиндрические соленоиды). Их называют нерегулярными соленоидами . Они нашли применение в различных областях, таких как соленоиды с редкой обмоткой для беспроводной передачи энергии , соленоиды с переменным шагом для магнитно-резонансной томографии (МРТ), и нецилиндрические соленоиды для других медицинских устройств.

Расчет собственной индуктивности и емкости невозможно выполнить, используя расчеты для обычных соленоидов, то есть с туго намотанными. Предложены новые методы расчета собственной индуктивности. (коды доступны на ) и емкость. (коды доступны на )

Индуктивность

См. Также: Индуктивность с физической симметрией.

Как показано выше, плотность магнитного потока $B$ внутри катушки практически постоянна и определяется выражением

$B=\mu _{0}{\frac {NI}{l}},$

где µ ₀ — магнитная постоянная , $N$ количество витков, $I$ текущий и $l$ длина катушки. Пренебрегая конечными эффектами, общий магнитный поток через катушку получается умножением плотности потока $B$ по площади поперечного сечения $A$:

$\Phi =\mu _{0}{\frac {NIA}{l}}.$

Объединив это с определением индуктивности

$L={\frac {N\Phi }{I}},$

индуктивность соленоида равна

$L=\mu _{0}{\frac {N^{2}A}{l}}.$

Таблица индуктивности коротких соленоидов с различным соотношением диаметра и длины была рассчитана Деллинджером, Уитмором и Оулдом.

Это значение, а также индуктивность более сложных форм можно вывести из уравнений Максвелла . Для катушек с жестким воздушным сердечником индуктивность зависит от геометрии катушки и количества витков и не зависит от тока.

Аналогичный анализ применим и к соленоиду с магнитопроводом, но только в том случае, если длина катушки много больше произведения относительной проницаемости магнитопровода на диаметр. Это ограничивает простой анализ сердечниками с низкой проницаемостью или чрезвычайно длинными тонкими соленоидами. Наличие сердечника можно учесть в приведенных выше уравнениях, заменив магнитную постоянную µ ₀ на µ или µ ₀ µ _r , где µ представляет проницаемость, а µ _r относительную проницаемость . Обратите внимание, что, поскольку проницаемость ферромагнитных материалов изменяется в зависимости от приложенного магнитного потока, индуктивность катушки с ферромагнитным сердечником обычно меняется в зависимости от тока.

См. также

• Катушка Гельмгольца
• Индуктор

Внешние ссылки

• Интерактивное руководство по Java: Магнитное поле соленоида , Национальная лаборатория сильных магнитных полей
• Обсуждение соленоидов в «Гиперфизике»